Class 12 RD Sharma Solutions – Chapter 24 Scalar or Dot Product – Exercise 24.1 | Set 1
Last Updated :
28 Mar, 2021
Question 1. Find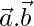 when
when
(i) 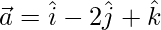 and
and 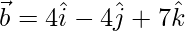
Solution:
= 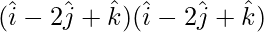
= (1)(4) + (-2)(-4) + (1)(7)
= 4 + 8 + 7
= 19
(ii) 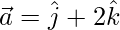 and
and 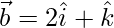
Solution:
= 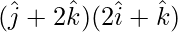
= (0)(2) + (1)(0) + (2)(1)
= 2
(iii) 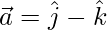 and
and 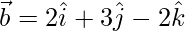
Solution:
= 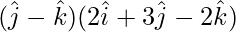
= (0)(2) + (1)(3) + (-1)(-2)
= 0 + 3 + 2
= 5
Question 2. For what value of λ are the vector  and
and 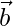 perpendicular to each other? where:
perpendicular to each other? where:
(i) 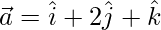 and
and 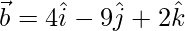
Solution:
 and
and 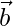 are perpendicular to each other
are perpendicular to each other
So 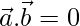
⇒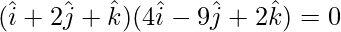
⇒ λ(4) + (2)(-9) + (1)(2) = 0
⇒ 4λ – 18 + 2 = 0
⇒ 4λ = 16
⇒ λ = 4
(ii) 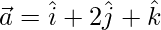 and
and 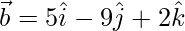
Solution:
 and
and 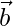 are perpendicular to each other
are perpendicular to each other
so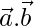 = 0
= 0
⇒ 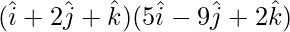
⇒ λ(5) + (2)(-9) + (1)(2) = 0
⇒ 5λ – 18 + 2 = 0
⇒ 5λ = 16
⇒ λ = 16/5
(iii) 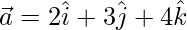 and
and 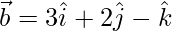
Solution:
 and
and 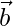 are perpendicular to each other
are perpendicular to each other
so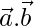 = 0
= 0
⇒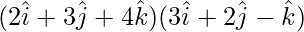 =0
=0
⇒ (2)(3) + (3)(2) – (4)λ = 0
⇒ 6 + 6 – 4λ = 0
⇒ 4λ = 12
⇒ λ = 3
(iv) 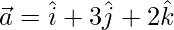 and
and 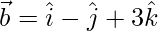
Solution:
 and
and 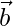 are perpendicular to each other
are perpendicular to each other
so 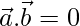
⇒ 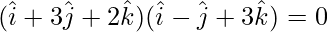
⇒ λ(1) + (3)(-1) + (2)(3) = 0
⇒ λ – 3 + 6 = 0
⇒ λ = 3
Question 3. If  and
and 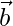 are two vectors such that |
are two vectors such that | |=4, |
|=4, |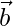 | = 3 and
| = 3 and 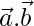 = 6. Find the angle between
= 6. Find the angle between 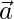 and
and 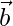
Solution:
Let the angle be θ
cos θ = 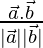
= 6 /(4×3) = 1/2
Therefore, θ = cos-1(1/2)
= π/3
Question 4. If 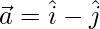 and
and 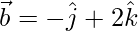 , find
, find 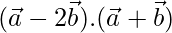 .
.
Solution:
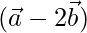 =
= 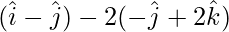
=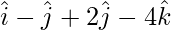
=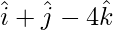
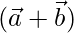 =
= 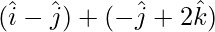
= 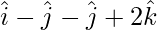
= 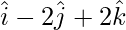
Now, 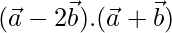
= 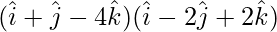
= (1)(1) + (1)(-2) + (-4)(2)
= 1 – 2 – 8
= -9
Therefore, 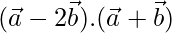 = -9
= -9
Question 5. Find the angle between the vectors  and
and 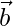 where :
where :
(i) 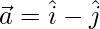 and
and 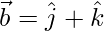
Solution:
Let the angle be θ between  and
and 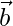
cos θ = 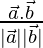
Now, 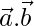
= 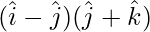
= (1)(0) + (-1)(1) + (0)(1)
= 0 – 1 + 0 = -1
| |= |
|= |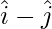 |
|
= 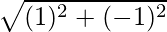
= √2
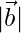 = |
= |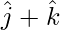 |
|
= 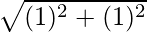
= √2
Now, cos θ = -1/(√2×√2)
= -1/2
θ = cos-1(-1/2)
= 2π/3
(ii) 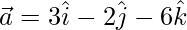 and
and 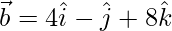
Solution:
Let the angle be θ between 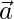 and
and 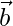
Now, 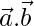
=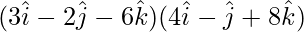
=(3)(4) + (-2)(-1) + (-6)(8)
= 12 + 2 – 48
= -34
|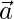 | = |
| = |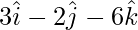 |
|
= 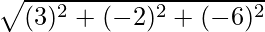
= √49 = 7
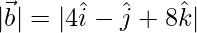
= 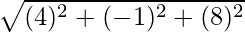
= √81 = 9
cos θ = 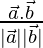
Now, cos θ = -34/(7×9)
= -34/63
θ = cos-1(-34/63)
(iii) 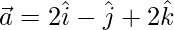 and
and 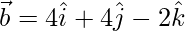
Solution:
Let the angle be θ between 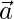 and
and 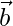
Now, 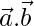
=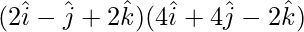
= (2)(4) + (-1)(4) + (2)(-2)
= 8 – 4 – 4 = 0
|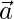 | = |
| = |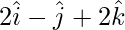 |
|
= 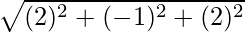
= √9 = 3
|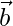 | = |
| = |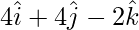 |
|
=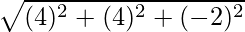
= √36 = 6
Now, cos θ = 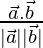
cos θ = 0/(3×6) = 0
θ = cos-1(0)
θ = π/2
(iv) 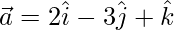 and
and 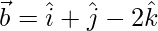
Solution:
Let the angle be θ between 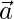 and
and 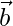
Now, 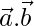
=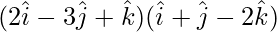
= (2)(1) + (-3)(1) + (1)(-2)
= 2 – 3 – 2
= -3
|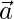 | =
| = 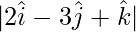
=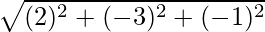
= √14
|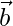 | =|
| =|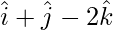 |
|
=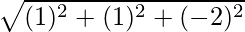
= √6
cos θ = 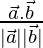
Now, cos θ = -3/(√14×√6)
= -3/√84
θ = cos-1(-3/√84)
(v) 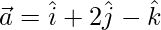 and
and 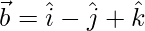
Solution:
Let the angle be θ between 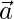 and
and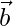
Now,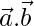
=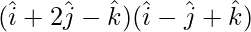
= (1)(1) + (2)(-1) + (-1)(1)
= 1 – 2 – 1
= -2
|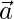 | = |
| = |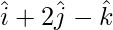 |
|
=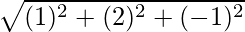
= √6
|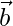 | = |
| = |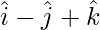 |
|
=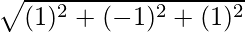
= √3
cos θ = 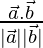
Now, cos θ = -2/(√6×√3)
= -2/√18
= -2/3√2
θ = cos-1(-√2 /3)
Question 6. Find the angles which the vectors 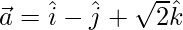 makes with the coordinate axes.
makes with the coordinate axes.
Solution:
Components along x, y and z axis are 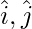 and
and 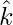 respectively.
respectively.
Let the angle between 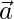 and
and 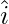 be θ1
be θ1
Now, 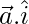
= 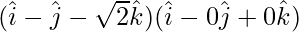
= (1)(1) + (-1)(0) + (√2)(0)
= 1
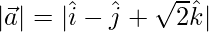
= 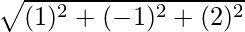
= √4 = 2
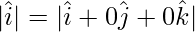
= √1 = 1
cos θ1 = 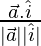
Now, cos θ1 = 1/(2×1)
= 1/2
θ1 = cos-1(1/2) = π/3
Let the angle between 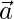 and
and 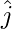 be θ2
be θ2
Now, 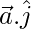
=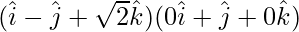
= (1)(0) + (-1)(1) + (√2)(0)
= -1
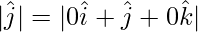
= √1 = 1
cos θ2 =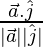
Now, cos θ2 = -1/(2×1)
= -1/2
θ2 = cos-1(-1/2) = 2π/3
Let the angle between 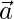 and
and 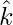 be θ3
be θ3
Now, 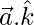
=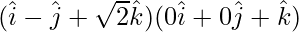
= (1)(0) + (-1)(0) + (√2)(1)
= √2
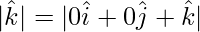
= √1 = 1
cos θ3 = 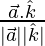
= 1/(√2)
= cos-1(1/√2) = π/4
Question 7(i). Dot product of a vector with 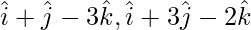 and
and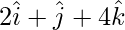 are 0, 5 and 8respectively. Find the vector.
are 0, 5 and 8respectively. Find the vector.
Solution:
Let 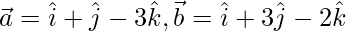 and
and 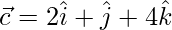 be three given vectors.
be three given vectors.
Let 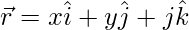 be a vector such that its dot products with
be a vector such that its dot products with 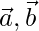 , and
, and 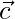 are 0, 5 and 8 respectively. Then,
are 0, 5 and 8 respectively. Then,
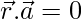
⇒ 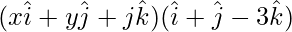 = 0
= 0
⇒ x + y – 3z = 0 ….(1)
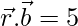
⇒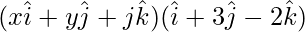 = 5
= 5
⇒ x + 3y – 2z = 5 …..(2)
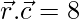
⇒ 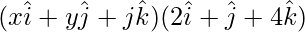 = 8
= 8
⇒ 2x + y + 4z = 8 …..(3)
Solving 1,2 and 3 we get x = 1, y = 2 and z = 1,
Hence, the required vector is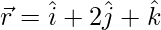
Question 8. If 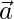 and
and 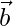 are unit vectors inclined at an angle θ then prove that
are unit vectors inclined at an angle θ then prove that
(i) cos θ/2 = 1/2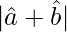
Solution:
|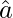 | = |
| = |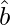 | = 1
| = 1
|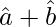 |2 =(
|2 =(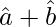 )2
)2
= 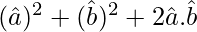
= 1 + 1 + 2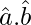
= 2 + 2|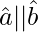 |cos θ
|cos θ
= 2(1 + (1)(1)cos θ)
= 2(2cos2 θ/2)
|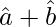 |2 = 4cos2 θ/2
|2 = 4cos2 θ/2
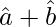 = 2 cos θ/2
= 2 cos θ/2
cos θ/2 = 1/2|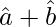 |
|
(ii) tan θ/2 = 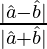
Solution:
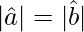 = 1
= 1
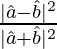 =
= 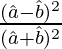
=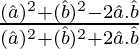
= 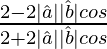
=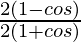
= 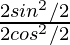
= tan2 θ/2
Therefore, tan θ/2 =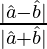
Question 9. If the sum of two unit vectors is a unit vector prove that the magnitude of their difference is √3.
Solution:
Let 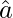 and
and 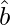 be two unit vectors
be two unit vectors
Then, 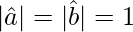
According to question:
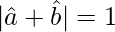
Taking square on both sides
⇒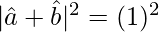
⇒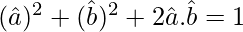
⇒ (1)2+(1)2+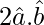 = 1
= 1
⇒ 2+ 2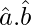 = 1
= 1
⇒ 2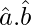 = -1
= -1
⇒ \hat{a}.\hat{b} =-1/2
Now, 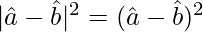
= 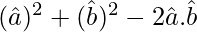
= (1)2 + (1)2 – 2 (-1/2)
= 2 + 1 = 3
Therefore, 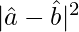 = 3
= 3
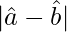 =√3
=√3
Question 10. If 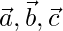 are three mutually perpendicular unit vectors, then prove that |
are three mutually perpendicular unit vectors, then prove that |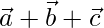 | =√3.
| =√3.
Solution:
Given 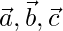 are mutually perpendicular so,
are mutually perpendicular so,
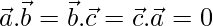
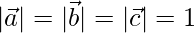
Now,
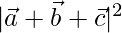 =
= 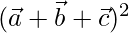
=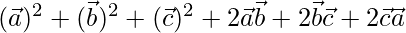
= (1)2 + (1)2 +(1)2 + 0
= 3
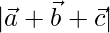 = √3
= √3
Question 11. If 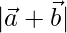 = 60,
= 60, 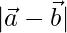 = 40 and
= 40 and 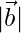 = 46, find
= 46, find 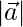
Solution:
Given 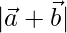 =60,
=60, 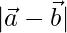 = 40 and
= 40 and 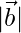 = 46
= 46
We know that,
(a + b)2 + (a – b)2 = 2(a2 + b2)
⇒ 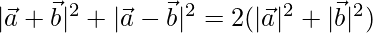
⇒ 602 + 402 = 2(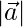 2 + 492)
2 + 492)
⇒ 3600 + 1600 = 2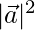 + 2401
+ 2401
⇒ 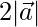 = 968
= 968
⇒ 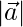 = √484 =22
= √484 =22
Question 12. Show that the vector 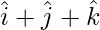 is equally inclined with the coordinate axes.
is equally inclined with the coordinate axes.
Solution:
Let 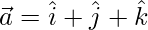
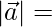 √(1+1+1) = √3
√(1+1+1) = √3
Let θ1, θ2, θ3 be the angle between the coordinate axes and the 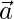
cos θ1 = 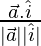
= 1/√3
cos θ2 = 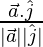
= 1/√3
cos θ3 = 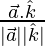
= 1/√3
Since, cos θ1 = cos θ2 = cos θ3
Therefore, Given vector is equally inclined with coordinate axis.
Question 13. Show that the vectors 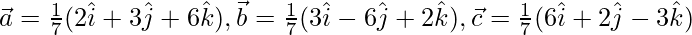 are mutually perpendicular unit vectors.
are mutually perpendicular unit vectors.
Solution:
Given, 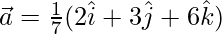
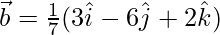
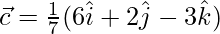
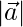 = (1/7)√(22 + 32 + 62) = (1/7)(√49) = 1
= (1/7)√(22 + 32 + 62) = (1/7)(√49) = 1
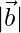 = (1/7)√(32 + (-6)2 + 22) = (1/7)(√49) = 1
= (1/7)√(32 + (-6)2 + 22) = (1/7)(√49) = 1
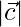 = (1/7)√(62 + 22 + (-3)2) = (1/7)(√49) = 1
= (1/7)√(62 + 22 + (-3)2) = (1/7)(√49) = 1
Now, 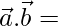 1/49[3 × 2 – 3 × 6 + 6 × 2]
1/49[3 × 2 – 3 × 6 + 6 × 2]
= 1/49[6 – 18 + 12] = 0
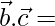 1/49[3 × 6 – 6 × 2 – 2 × 3]
1/49[3 × 6 – 6 × 2 – 2 × 3]
= 1/49[18 – 12 – 6] = 0
Since, 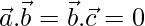 they are mutually perpendicular unit vectors.
they are mutually perpendicular unit vectors.
Question 14. For any two vectors  and
and 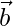 , Show that
, Show that 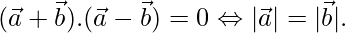
Solution:
To prove 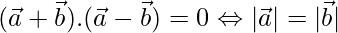
⇒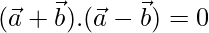
⇒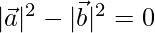
⇒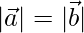
Hence Proved
Question 15. If 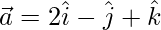 ,
, 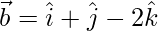 and
and 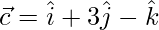 , find such that
, find such that 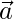 is perpendicular to
is perpendicular to 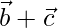 .
.
Solution:
Given: 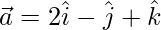
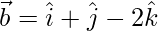
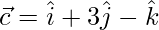
According to question
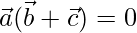
⇒ ![Rendered by QuickLaTeX.com (2\hat{i}-\hat{j}+\hat{k})[λ(\hat{i}+\hat{j}-2\hat{k})+(\hat{i}+3\hat{j}-\hat{k})]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-90e6050701d1970a9aa2f3fbb2f92f89_l3.png)
⇒ 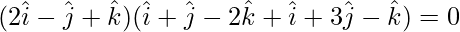
⇒ 2(λ+1) – (λ+3) -2λ-1 = 0
⇒ 2λ + 2 -λ – 3 – 2λ – 1 = 0
⇒ -λ = 2
⇒ λ = -2
Question 16. If 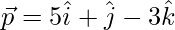 and
and 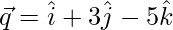 , then find the value of λ so that
, then find the value of λ so that 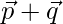 and
and 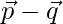 are perpendicular vectors.
are perpendicular vectors.
Solution:
Given, 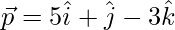
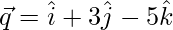
According to question
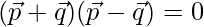
⇒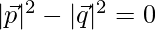
⇒ 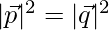
⇒ 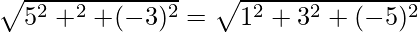
⇒ 25 + λ2 + 9 = 1 + 9 + 25
⇒ λ2 = 1
⇒ λ = 1
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...