Class 12 RD Sharma Solutions- Chapter 19 Indefinite Integrals – Exercise 19.12
Last Updated :
03 May, 2022
Question 1. ∫sin4x cos3x dx
Solution:
Let I = ∫ sin4x cos3x dx -(i)
Let sinx = t
On differentiating with respect to x:
cosx = dt/dx
cosx dx = dt
dx = dt/cosx
Putting value of dx and sinx in equation (i):
I = ∫ t4 cosxdt/cosx
I = ∫ t4 cos2 x dt
I = ∫ t4 (1 – sin2 x) dt
I = ∫ t4 (1 – t2) dt
I = ∫ (t4– t2) dt
I = t5/5 – t7/7 + c
I = sin5/5 – sin7/7 + c
Question 2. ∫ sin5x dx
Solution:
Let I = ∫ sin5x dx
I = ∫sin3xsin2x dx
= ∫sin3x(1 – cos2x)dx
= ∫(sin3x – sin3xcos2x)dx
= ∫[sinxsin2x – sin3xcos2x]dx
= ∫[sinx(1 – cos2x) – sin3xcos2x]dx
= ∫(sinx – sinxcos2x – sin3xcos2x)dx
I = ∫sinx dx – ∫sinxcos2x dx – ∫sin3xcos2x dx
Putting cosx = t and -sinxdx = dt in 2nd and 3rd integral:
I = ∫sinx dx + ∫t2dt + ∫sin2xt3dt/t
= ∫sinx dx + ∫t2 dt + ∫sin2xt2 dt
= ∫sinx dx + ∫t2 dt + ∫(1 – cos2x)t2 dt
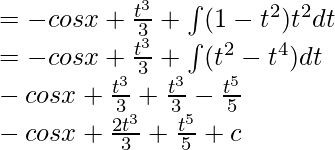 Putting value of t:
Putting value of t: 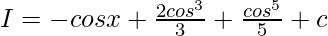
Question 3. ∫cos5x dx
Solution:
Let I = ∫cos5x dx
I = ∫cos2xcos3x dx
= ∫(1 – sin2x)cos3x dx
= ∫(cos3x−sin2xcos3x)dx
= ∫(cos2xcosx – sin2xcos2xcosx)dx
= ∫[(1 – sin2x)cosx – sin2x(1 – sin2x)cosx]dx
= ∫(cosx – sin2xcosx – sin2xcosx + sin4xcosx)dx
= ∫cosx dx – 2∫sin2xcosx dx + ∫sin4xcosx dx
Putting sinx = t and cosxdx = dt in 2nd and 3rd integral we get:
I = ∫cos dx – 2∫t2dt + ∫t4dt
= sinx – 2t3/3 + t5/5 + c
Putting value of t:
I = = sinx – 2sin3x/3 + cos5x/5 + c
Question 4. ∫sin5xcosx dx
Solution:
Let I = ∫sin5xcosx dx −(i)
Let sinx = t:
On differentiating with respect to x:
-cosx = dt/dx
cosx dx = -dt
Putting cosxdx = -dt and sinx = t in eq (i):
I = ∫t5dt
= t6/6 + c
= sin6x/6 + c
Question 5. ∫sin3xcos6x dx
Solution:
Let I = ∫sin3xcos6x dx −(i)
Let cosx = t
On differentiating both sides w.r.t′x′:
-sinx = dt/dx
sinxdx = -dt
Putting cosx = t and sinxdx = -dt in eq (i):
I = -∫sin2x t6dt
= -∫(1 – cos2x)t6dt
= -∫(1 – t2)t6dt
= -∫(t6 – t8)dt
= -(t7/7 – t9/9) + c
Putting value of t:
I = -(cos7x/7 – cos9x/9) + c
Question 6. ∫cos7x dx
Solution:
Let I = ∫cos7x dx
= ∫cos6xcosx dx
= ∫(cos2x)3cosx dx
= ∫(1 – sin2x)3cosx dx
= ∫(1 – sin6x – 3sin2x + 3sin4x)cosx dx
= ∫(cosx – sin6xcosx – 3sin2xcosx + 3sin4xcosx)dx −(i)
Putting sinx = t and cosx dx = t in 2nd,3rd and 4th integral in (i):
I = ∫cosx dx – ∫t6dt – 3∫t2dt + 3∫t4dt
= sinx – t7/7 - 3t3/3 +3t5/5 + c
Putting value of t:
= sinx – sin7x/7 - 3sin3x/3 +3sin5x/5 + c
Question 7. ∫xcos3x2sinx2dx
Solution:
Let I = ∫xcos3x2sinx2dx −(i)
Let cosx2 = t
On differentiating both sides:
-2xsinx2 = dt/dx
xsinx2 dx = -dt/2
Putting values in (i):
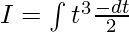
= -t4/8 + c
Putting value of t:
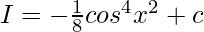
Question 8. ∫sin7x dx
Solution:
Let I = ∫sin7x dx
I = ∫sin6x sinx dx
= ∫(sin2x)3sinx dx
= ∫(1 – cos2x)3sinx dx
= ∫(1 – cos6x – 3cos2x + 3cos4x)sinx dx
I = ∫sinx dx – ∫cos6xsinx dx + 3∫cos4xsinx dx – 3∫cos2xsinx dx
Putting cosx = t and sinx dx = -dt in 2nd,3rd and 4th integral:
I = ∫sinx dx – ∫t6(-dt) + 3∫t4(-dt) – 3∫t2(-dt)
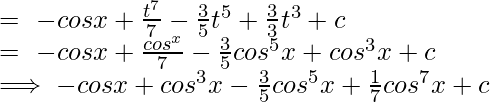
Question 9. ∫sin3xcos5x dx
Solution:
Let I = ∫sin3xcos5x dx −(i)
Let cosx = t
On differentiating both sides: -sinx = dt/dx
sinx dx = -dt
Putting values in (i):
I = ∫sin2xt5(-dt)
= −∫(1 – cos2x)t5 dt
= −∫(1 – t2)t5 dt
= ∫(t7 – t5) dt
= t8/8 – t6/6 + c
Putting value of t:
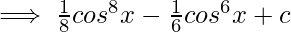
Question 10. 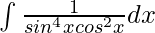
Solution:
Let I = 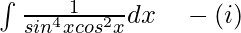
Dividing and multiplying the equation by cos6x:
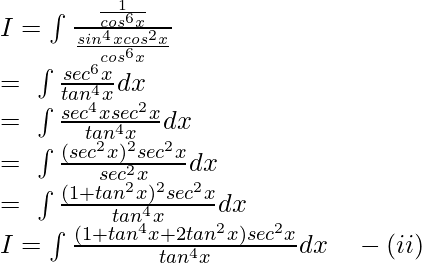
Let tanx = t, then:
sec2x = dt/dx
sec2x dx = dt
Putting values in eq (ii):
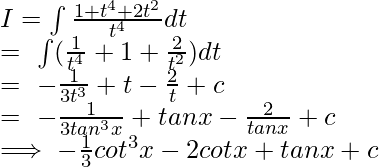
Question 11. 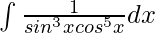
Solution:
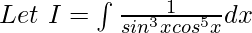 Dividing and multiplying by cos8x:
Dividing and multiplying by cos8x: 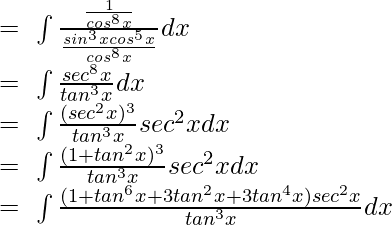 Let tanx=t,then:
Let tanx=t,then: 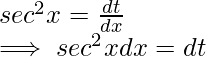 Putting values in ii:
Putting values in ii: 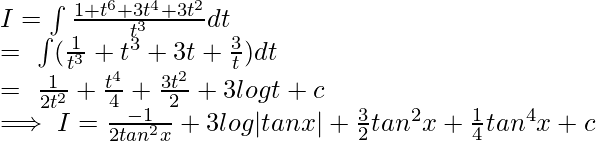
Question 12. 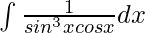
Solution:
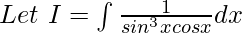 Dividing and multiplying by cos4x:
Dividing and multiplying by cos4x: 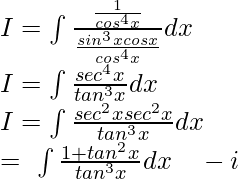 Let tanx=t,then: sec2xdx = dt Putting values in i:
Let tanx=t,then: sec2xdx = dt Putting values in i: 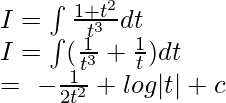 Putting value of t:
Putting value of t: 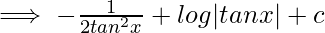
Question 13. 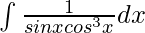
Solution:
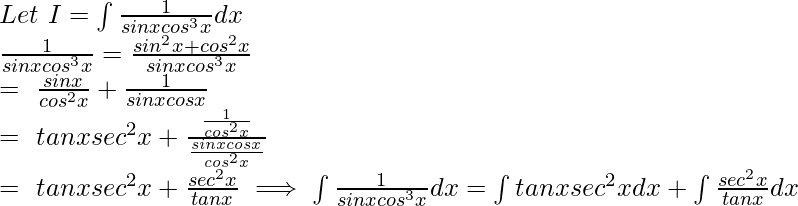 Let tanx=t⟹sec2x dx = dt:
Let tanx=t⟹sec2x dx = dt: 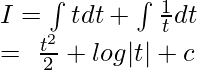 Putting value of t:
Putting value of t: 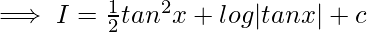
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...