Class 12 RD Sharma Solutions – Chapter 5 Algebra of Matrices – Exercise 5.3 | Set 2
Last Updated :
21 Jul, 2021
Question 26. If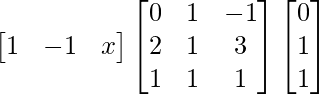 = 0, find x.
= 0, find x.
Solution:
We have,
=>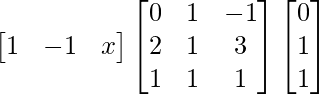 = 0
= 0
=>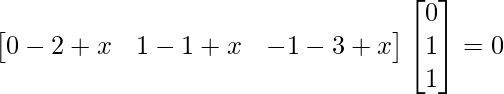
=>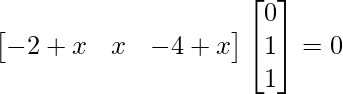
=>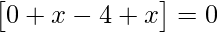
=> 2x – 4 = 0
=> 2x = 4
=> x = 2
Therefore, the value of x is 2.
Question 27. If A =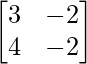 and I =
and I = , then prove that A2 – A + 2I = 0.
, then prove that A2 – A + 2I = 0.
Solution:
We have,
A =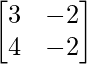
A2 =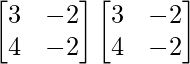
=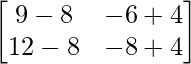
=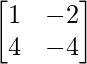
L.H.S. = A2 – A + 2I
=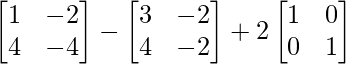
=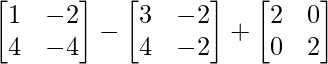
=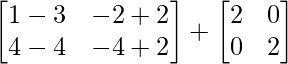
=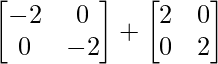
=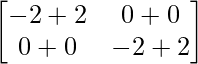
=
= 0
= R.H.S.
Hence proved.
Question 28. If A =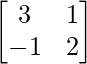 and I =
and I = , then find λ so that A2 = 5A + λI.
, then find λ so that A2 = 5A + λI.
Solution:
We have,
A =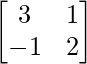
A2 =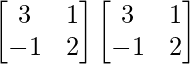
=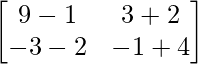
=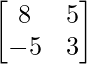
We are given,
=> A2 = 5A + λI
=>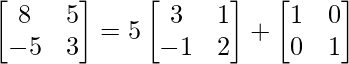
=>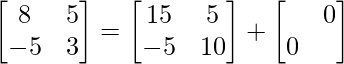
=>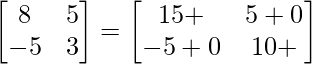
=>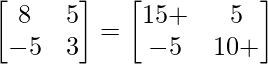
On comparing both sides, we get
=> 8 = 15 + λ
=> λ = –7
Therefore, the value of λ is –7.
Question 29. If A =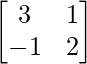 , show that A2 – 5A + 7I2 = 0.
, show that A2 – 5A + 7I2 = 0.
Solution:
We have,
A =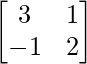
A2 =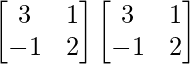
=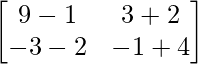
=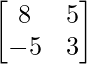
L.H.S. = A2 – 5A + 7I2
=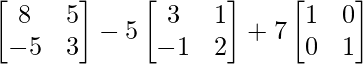
=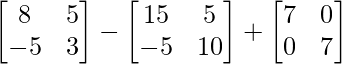
=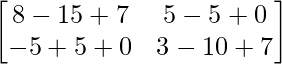
=
= 0
= R.H.S.
Hence proved.
Question 30. If A =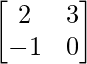 , show that A2 – 2A + 3I2 = 0.
, show that A2 – 2A + 3I2 = 0.
Solution:
We have,
A =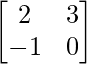
A2 =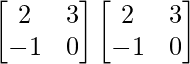
=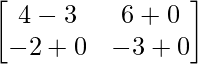
=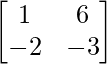
L.H.S. = A2 – 2A + 3I2
=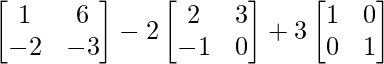
=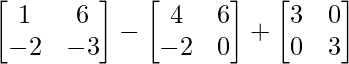
=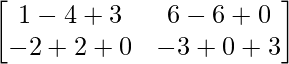
=
= 0
= R.H.S.
Hence proved.
Question 31. Show that the matrix A = satisfies the equation A3 – 4A2 + A = 0.
satisfies the equation A3 – 4A2 + A = 0.
Solution:
We have,
A =
A2 =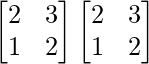
=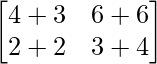
=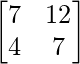
A3 = A2. A
=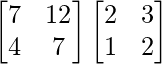
=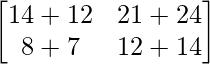
=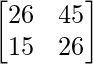
L.H.S. = A3 – 4A2 + A
=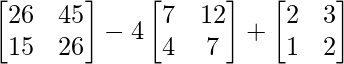
=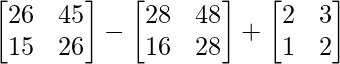
=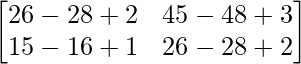
=
= 0
= R.H.S.
Hence proved.
Question 32. Show that the matrix A =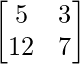 is root of the equation A2 – 12A – I = 0
is root of the equation A2 – 12A – I = 0
Solution:
We have,
A =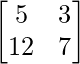
A2 =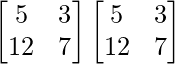
=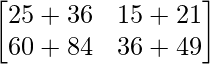
=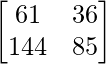
L.H.S. = A2 – 12A – I
=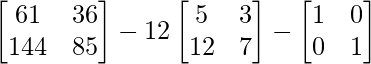
=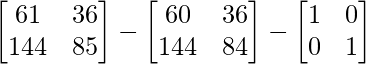
=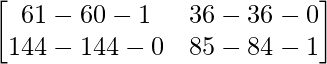
=
= 0
= R.H.S.
Hence proved.
Question 33. If A =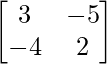 find A2 – 5A – 14I.
find A2 – 5A – 14I.
Solution:
We have,
A =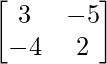
A2 =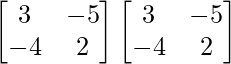
=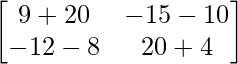
=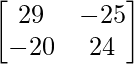
A2 – 5A – 14I =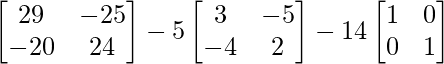
=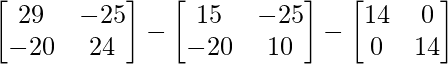
=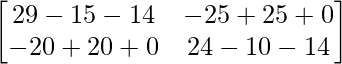
=
Question 34. If A =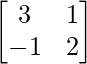 , find A2 – 5A + 7I = 0. Use this to find A4.
, find A2 – 5A + 7I = 0. Use this to find A4.
Solution:
We have,
A =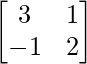
A2 =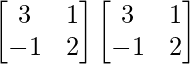
=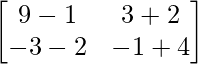
=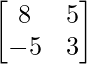
L.H.S. = A2 – 5A + 7I = 0
=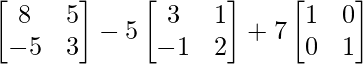
=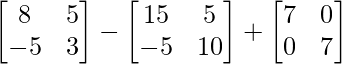
=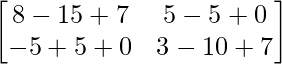
=
= 0
= R.H.S.
Hence proved.
Now we have A2 – 5A + 7I = 0
=> A2 = 5A – 7I
=> A4 = (5A – 7I) (5A – 7I)
=> A4 = 25A2 – 35AI – 35AI + 49I
=> A4 = 25A2 – 70AI + 49I
=> A4 = 25 (5A – 7I) – 70AI + 49I
=> A4 = 125A – 175I – 70A + 49I
=> A4 = 55A – 126I
=> A4 =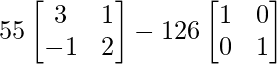
=> A4 =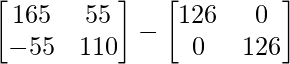
=> A4 =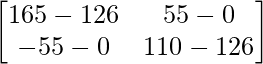
=> A4 =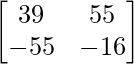
Question 35. If A =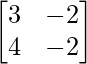 , find k such that A2 = kA – 2I2.
, find k such that A2 = kA – 2I2.
Solution:
We have,
A =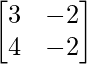
A2 =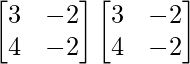
=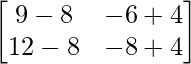
=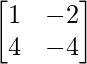
We are given,
=> A2 = kA – 2I2
=>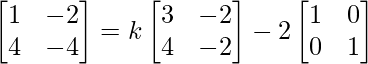
=>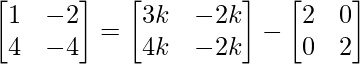
=>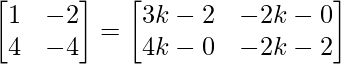
On comparing both sides, we get
=> 3k – 2 = 1
=> 3k = 3
=> k = 1
Therefore, the value of k is 1.
Question 36. If A =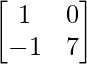 , find k such that A2 – 8A + kI = 0.
, find k such that A2 – 8A + kI = 0.
Solution:
We have,
A =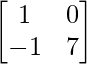
A2 =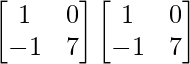
=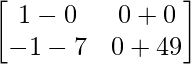
=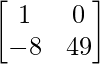
We are given,
=> A2 – 8A + kI = 0
=>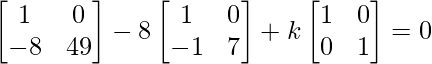
=>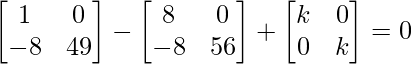
=>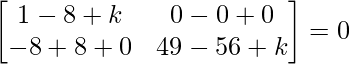
=>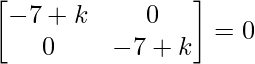
On comparing both sides, we get
=> –k + 7 = 0
=> k = 7
Therefore, the value of k is 7.
Question 37. If A =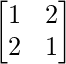 and f(x) = x2 – 2x – 3, show that f(A) = 0.
and f(x) = x2 – 2x – 3, show that f(A) = 0.
Solution:
We have,
A = and f(x) = x2 – 2x – 3
and f(x) = x2 – 2x – 3
A2 =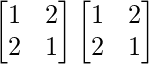
=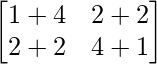
=
L.H.S. = f(A) = A2 – 2A – 3I2
=
=
=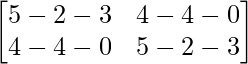
=
= 0
= R.H.S.
Hence proved.
Question 38. If A = and I =
and I = , find λ, μ so that A2 = λA + μI.
, find λ, μ so that A2 = λA + μI.
Solution:
We have,
A =
A2 =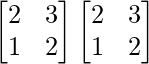
=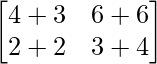
=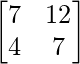
We are given,
=> A2 = λA + μI
=>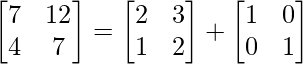
=>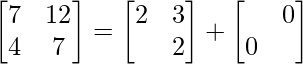
=>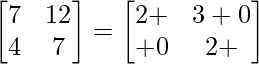
=>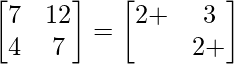
On comparing both sides, we get,
=> 2λ + μ = 7 and λ = 4
=> 2(4) + μ = 7
=> μ = 7 – 8
=> μ = –1
Therefore, the value of λ is 4 and μ is –1.
Question 39. Find the value of x for which the matrix product equals an identity matrix.
equals an identity matrix.
Solution:
We have,
=>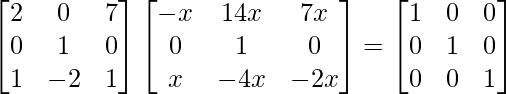
=>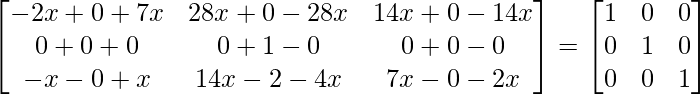
=>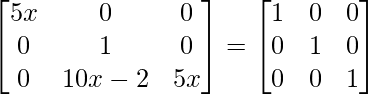
On comparing both sides, we get,
=> 5x = 1
=> x = 1/5
Therefore, the value of x is 1/5.
Question 40. Solve the following matrix equations:
(i)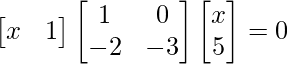
Solution:
We have,
=>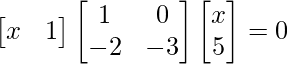
=>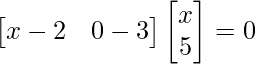
=>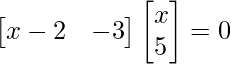
=>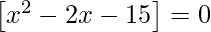
=> x2 – 2x – 15 = 0
=> x2 – 5x + 3x – 15 = 0
=> x (x – 5) + 3 (x – 5) = 0
=> (x – 5) (x + 3) = 0
=> x = 5 or –3
Therefore, the value of x is 5 or –3.
(ii)
Solution:
We have,
=>
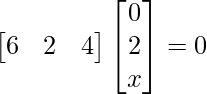
=>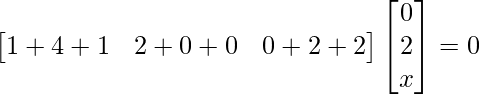
=>
=>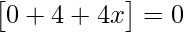
=> 4 + 4x = 0
=> 4x = –4
=> x = –1
Therefore, the value of x is –1.
(iii)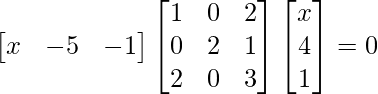
Solution:
We have,
=>
=>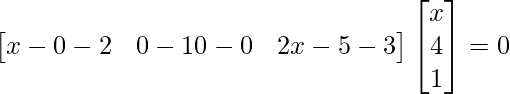
=>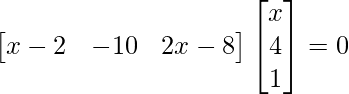
=>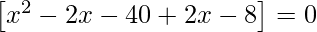
=> x2 – 48 = 0
=> x2 = 48
=> x = ±4√3
Therefore, the value of x is ±4√3.
(iv)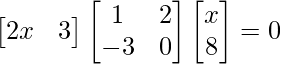
Solution:
We have,
=>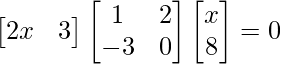
=>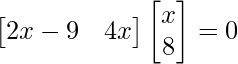
=>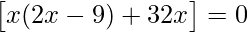
=>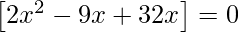
=> 2x2 + 23x = 0
=> x (2x + 23) = 0
=> x = 0 or x = –23/2
Therefore, the value of x is 0 or –23/2.
Question 41. If A =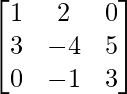 , compute A2 – 4A + 3I3.
, compute A2 – 4A + 3I3.
Solution:
We have,
A =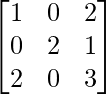
A2 =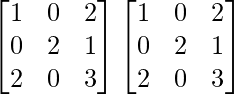
=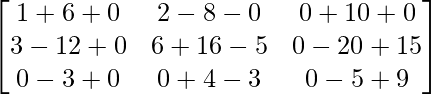
=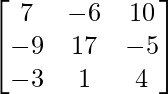
So, A2 – 4A + 3I3 =
=
=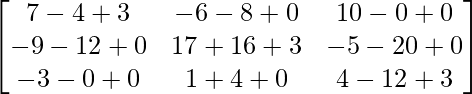
=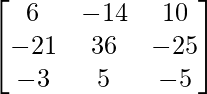
Question 42. If f(x) = x2 – 2x, find f(A), where A =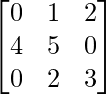 .
.
Solution:
We have,
A =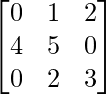 and f(x) = x2 – 2x
and f(x) = x2 – 2x
A2 =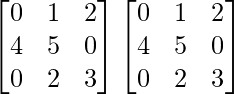
=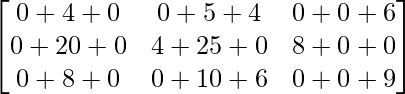
=
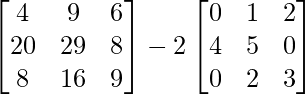
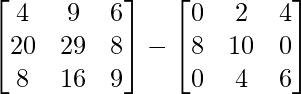
So, f(A) = A2 – 2A
=
=
=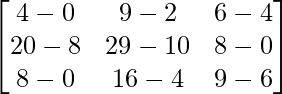
=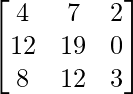
Question 43. If f(x) = x3 + 4x2 – x, find f(A) where A =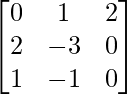 .
.
Solution:
We have,
A =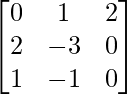 and f(x) = x3 + 4x2 – x
and f(x) = x3 + 4x2 – x
A2 =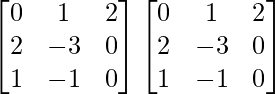
=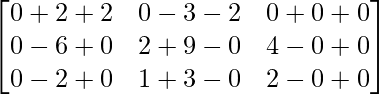
=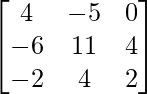
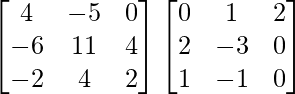
A3 = A2. A
=
=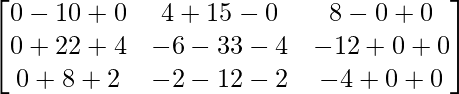
=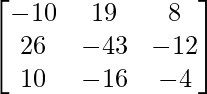
Now, f(A) = A3 + 4A2 – A
=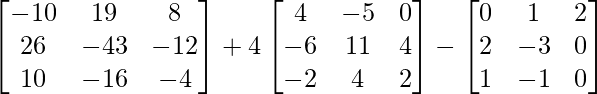
=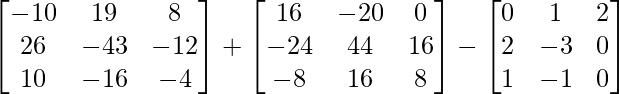
=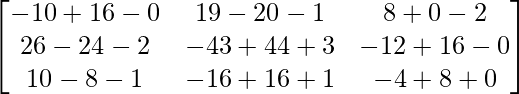
=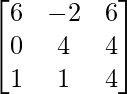
Question 44. If A =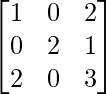 , then show that A is a root of the polynomial f(x) = x3 – 6x2 + 7x +2.
, then show that A is a root of the polynomial f(x) = x3 – 6x2 + 7x +2.
Solution:
We have,
A =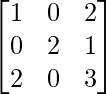 and f(x) = x3 – 6x2 + 7x +2.
and f(x) = x3 – 6x2 + 7x +2.
A2 =
=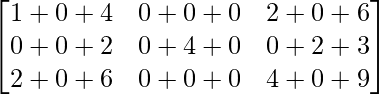
=
A3 = A2. A
=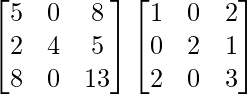
=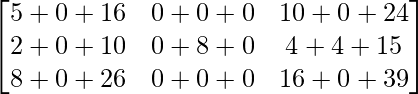
=
In order to show that A is a root of above polynomial, we need to prove that f(A) = 0.
Now, f(A) = A3 – 6A2 + 7A + 2I
=
=
=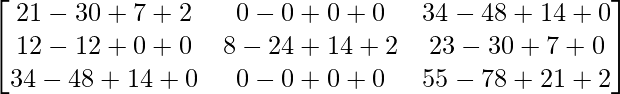
=
= 0
Hence proved.
Question 45. If A =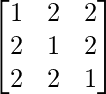 , prove that A2 – 4A – 5I = 0.
, prove that A2 – 4A – 5I = 0.
Solution:
We have,
A =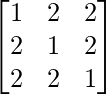
A2 =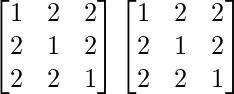
=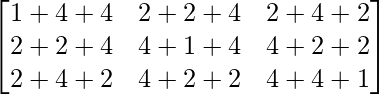
=
Now, L.H.S. = A2 – 4A – 5I
=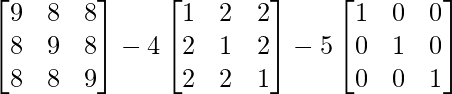
=
=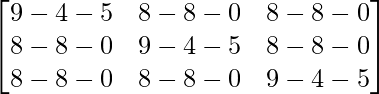
=
= 0
= R.H.S.
Hence proved.
Question 46. If A =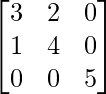 , show that A2 – 7A + 10I3 = 0.
, show that A2 – 7A + 10I3 = 0.
Solution:
We have,
A =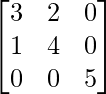
A2 =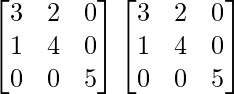
=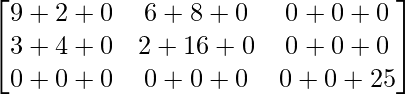
=
Now, L.H.S. = A2 – 7A + 10I3
=
=
=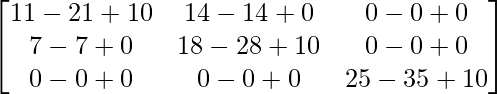
=
= 0
= R.H.S.
Hence proved.
Question 47. Without using the concept of inverse of a matrix, find the matrix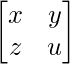 such that,
such that,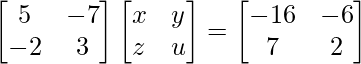
Solution:
We have,
=>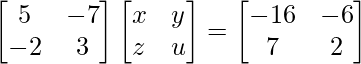
=>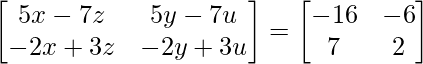
On comparing both sides, we get,
5x – 7z = –16
5y – 7u = –6
–2x + 3z = 7
–2y + 3u = 2
On solving the above equations, we get
=> x = 1, y = –4, z = 3 and u = –2.
So, we get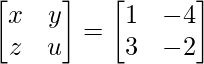 .
.
Question 48. Find the matrix A such that
(i)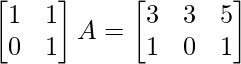
Solution:
Let A =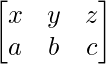
Given equation is,
=>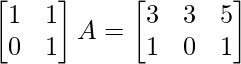
=>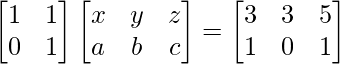
=>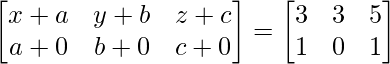
=>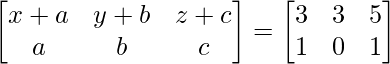
On comparing both sides, we get, a = 1, b = 0 and c = 1.
And x + 1 = 3 => x = 2
Also, y = 3 and
z + 1 = 5 => z = 4
So, we have A =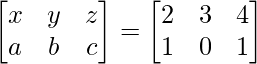
(ii)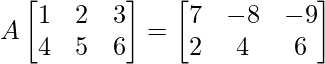
Solution:
Let A =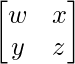
Given equation is,
=>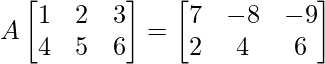
=>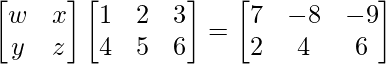
=>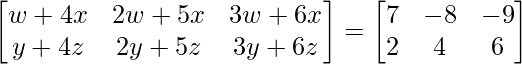
On comparing both sides, we get,
w + 4x = 7
2w + 5x = –6
y + 4z = 2
2y + 5z = 4
On solving the above equations, we get
=> x = –2, y = 2, w = 1 and z = 0.
So, we get A =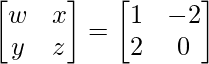
(iii)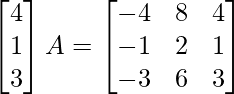
Solution:
Let A =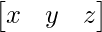
Given equation is,
=>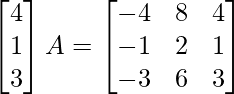
=>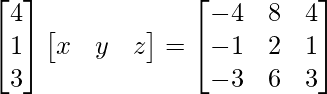
=>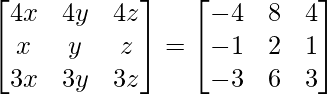
On comparing both sides, we get,
=> 4x = – 4, 4y = 8 and 4z = 4.
=> x = –1, y = 2 and z = 1.
So, we get A =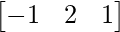
(iv)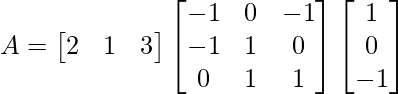
Solution:
We have,
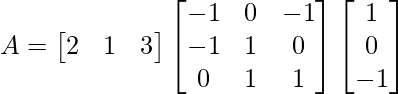
A =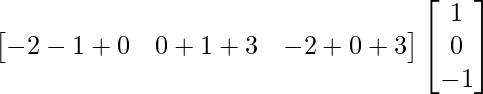
A =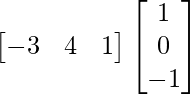
A =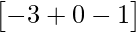
A =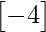
(v)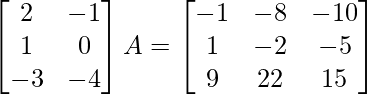
Solution:
Let A =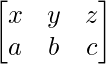
Given equation is,
=>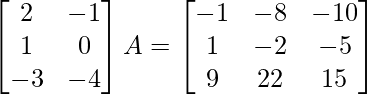
=>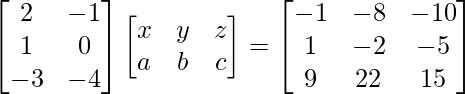
=>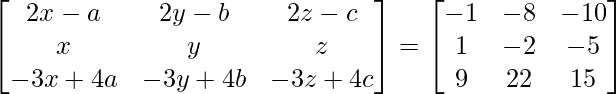
On comparing both sides, we get,
=> x = 1, y = –2 and z = –5
And also we have,
2x – a = –1
2y – b = –8
2z – c = –10
On solving these, we get,
=> a = 3, b = 4 and c = 0.
So, we get A =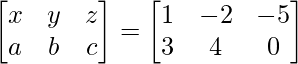
(vi)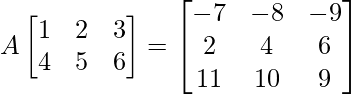
Solution:
Let A =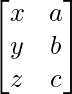
Given equation is,
=>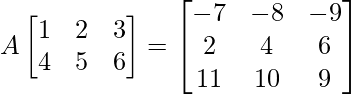
=>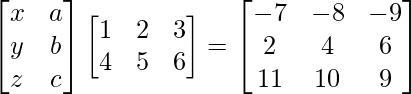
=>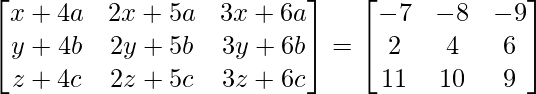
On comparing both sides, we get
x + 4a = –7 and 2x + 5a = –8
=> x = 1 and a = –2
y + 4b = 2 and 2y + 5b = 4
=> b = 0 and y = 2
z + 4c = 11 and 2z + 5c = 10
=> c = 4 and z = –5
So, we get A =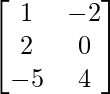
Question 49. Find a 2 × 2 matrix A such that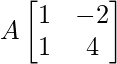 = 6I2.
= 6I2.
Solution:
Let A =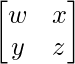
Given equation is,
=>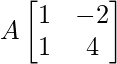 = 6I
= 6I
=>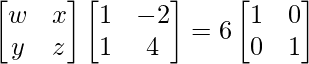
=>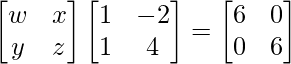
=>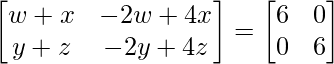
On comparing both sides, we get
w + x = 6 and –2w + 4x = 0
=> w = 4 and x = 2
y + z = 0 and –2y + 4z = 6
=> y = –1 and z = 1
So, we get A =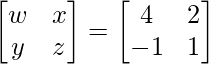
Question 50. If A = , find A16.
, find A16.
Solution:
We have,
A =
A2 =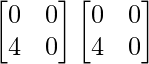
=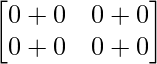
=
A16 = A2 A2 A2 A2
=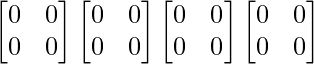
=
Question 51. If A =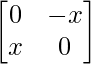 , B =
, B = and x2 = –1, then show that (A + B)2 = A2 + B2.
and x2 = –1, then show that (A + B)2 = A2 + B2.
Solution:
We have,
A =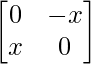 , B =
, B = and x2 = –1
and x2 = –1
L.H.S. = (A + B)2
=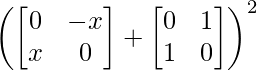
=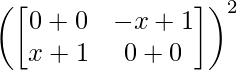
=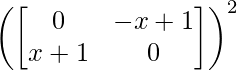
=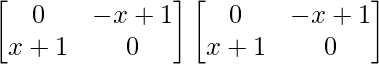
=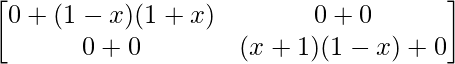
=
=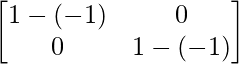
=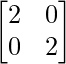
R.H.S. = A2 + B2
=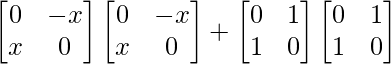
=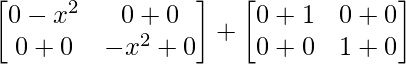
=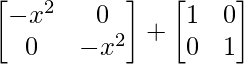
=
=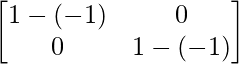
=
= L.H.S.
Hence proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...