Class 12 RD Sharma Solutions – Chapter 29 The Plane – Exercise 29.5
Last Updated :
11 Feb, 2021
Question 1. Find the vector equation of the plane passing through the points (1, 1, 1), (1, -1, 1) and (-7, -3, -5)
Solution:
Given that, plane is passing through
(1, 1, 1), (1, -1, 1) and (-7, -3, -5)
We know that, equation of plane passing through 3 points,
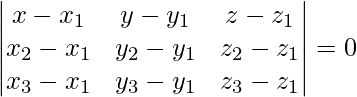
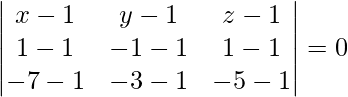
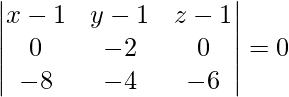
(x – 1)(12 – 0) – (y – 1)(0 – 0) + (z – 1)(0 – 16) = 0
(x – 1)(12) – (y – 1)(0) + (z – 1)(-16) = 0
12x – 12 – 0 – 16z + 16 = 0
12x – 16z + 4 = 0
Dividing by 4,
3x – 4z + 1 = 0
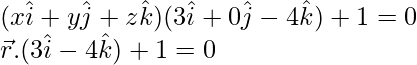
Equation of the required plane,

Question 2. Find the vector equation of the plane passing through the points P(2, 5, -3), Q(-2, -3, 5) and R(5, 3, -3).
Solution:
Let P(2, 5, -3), Q(-2, -3, 5) and R(5, 3, -3) be the three points on a plane having position vectors 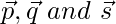 respectively. Then the vectors
respectively. Then the vectors 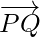 and
and 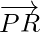 are in the same plane. Therefore,
are in the same plane. Therefore, 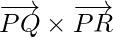 is a vector perpendicular to the plane.
is a vector perpendicular to the plane.
Let = 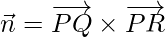
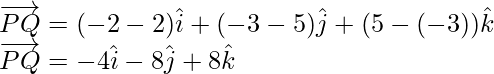
Similarly,
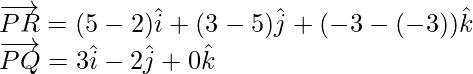
Thus
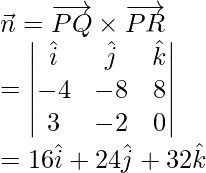
The plane passes through the point P with position vector 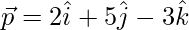
Thus, its vector equation is
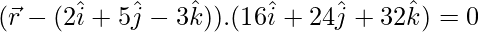
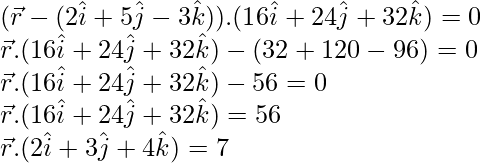
Question 3. Find the vector equation of the plane passing through the points A(a, 0, 0), B(0, b, 0) and C(0, 0, c). Reduce it to normal form. If plane ABC is at a distance p from origin, prove that 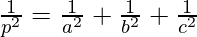
Solution:
Let A(a, 0, 0), B(0, b, 0) and C(0, 0, c) be three points on a plane having their position vectors 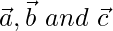 respectively. Then vectors
respectively. Then vectors 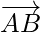 and
and 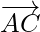 are in the same plane. Therefore,
are in the same plane. Therefore, 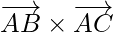 is a vector perpendicular to the plane.
is a vector perpendicular to the plane.
Let 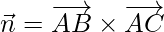
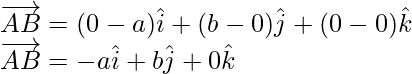
Similarly,
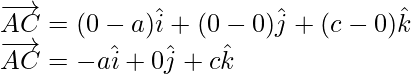
Thus
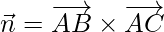
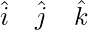
= | -a b 0 |
-a 0 c
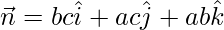
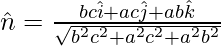
The plane passes through the point P with position vector 
Thus, the vector equation in the normal form is
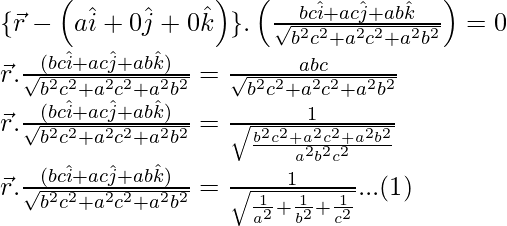
The vector equation of a plane normal to the unit vector 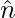 and at a distance ‘d’ from the origin is
and at a distance ‘d’ from the origin is  ….(2).
….(2).
Given that the plane is at a distance ‘p’ from the origin.
Comparing equations (1) and (2), we have,
d = p = 
Question 4. Find the vector equation of the plane passing through the points (1, 1, -1), (6, 4, -5) and (-4, -2, 3).
Solution:
Let P(1, 1, -1), Q(6, 4, -5) and R(-4, -2, 3) be three points on a plane having position vectors  respectively. Then the vectors
respectively. Then the vectors 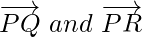 are in the same plane. Therefore,
are in the same plane. Therefore, 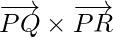 is a vector perpendicular to the plane.
is a vector perpendicular to the plane.
Let 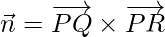
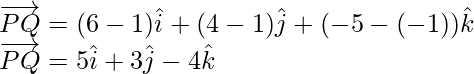
Similarly,
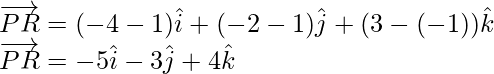
Thus
Here, 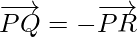
Therefore, the given points are collinear.
Thus,  where, 5a + 3b – 4c = 0
where, 5a + 3b – 4c = 0
The plane passes through the point P with position vector 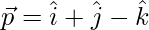
Thus, its vector equation is
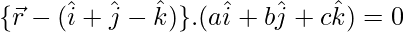 , where, 5a + 3b – 4c = 0
, where, 5a + 3b – 4c = 0
Question 5. Find the vector equation of the plane passing through the points
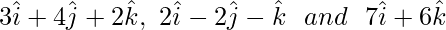
Solution:
Let A, B, C be the points with position vector 
respectively. Then
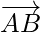 = Position vector of B – Position vector of A
= Position vector of B – Position vector of A
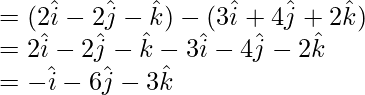
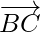 = Position vector of C – Position vector of B
= Position vector of C – Position vector of B
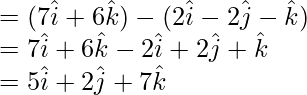
A vector normal to A, B, C is a vector perpendicular to 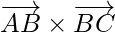

As we know that, equation of a plane passing through vector 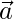 and perpendicular to vector
and perpendicular to vector 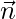 is given by,
is given by,
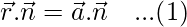
Put 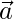 and
and 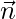 in equation (1)
in equation (1)
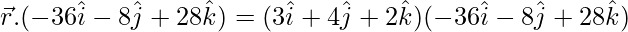
= (3)(-36) + (4)(-8) + (2)(28)
= -108 – 32 + 56
= -140 + 56
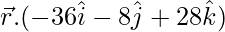 = -84
= -84
Dividing by (-4), we will get
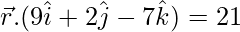
Equation of required plane is,
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...