Class 12 RD Sharma Solutions – Chapter 23 Algebra of Vectors – Exercise 23.4
Last Updated :
21 Feb, 2021
Question 1. If O is a point in space, ABC is a triangle, and D, E, F are the mid-points of the sides BC, CA, and AB respectively of the triangle, prove that
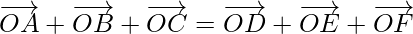
Solution:

In the △ABC, D, E, F are the mid points of the sides of BC, CA and AB and O is any point in space.
Let us considered 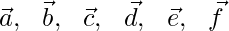 be the position vector of point A, B, C, D, E, F with respect to O.
be the position vector of point A, B, C, D, E, F with respect to O.
Therefore, 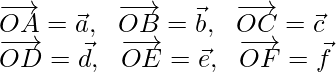
So, according to the mid-point formula
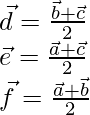
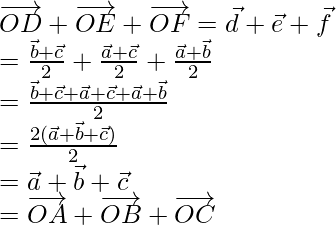
Hence, proved
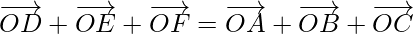
Question 2. Show that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.

Solution:
Let us considered ABC is triangle, so the position vector of A, B and C are 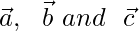
Hence, AD, BE, CF are medium, so, D, E and F are mid points of line BC, AC, and AB.
Now, using mid point formula we get
Position vector of D = 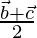
Position vector of E = 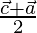
Position vector of F = 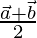
Now, add all the three median
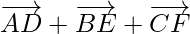
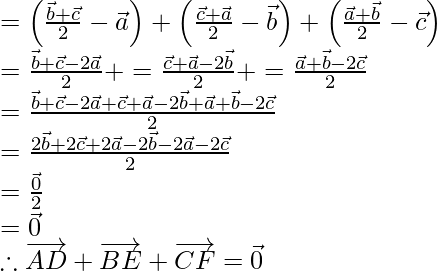
Hence, proved that the sum of the three vectors determined by the medians
of a triangle directed from the vertices is zero.
Question 3. ABCD is a parallelogram and P is the point of intersection of its diagonals. If O is the origin of reference, show that 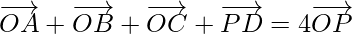

Solution:
Given that ABCD is a parallelogram, P is the point of intersection of diagonals and O be the point of reference.
So, by using triangle law in △AOP, we get
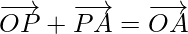 -(1)
-(1)
By using triangle law in △OBP, we get
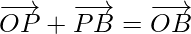 -(2)
-(2)
By using triangle law in △OPC, we get
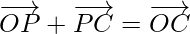 -(3)
-(3)
By using triangle law in △OPD, we get
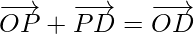 -(4)
-(4)
Now, on adding equation (1), (2), (3) and (4), we get
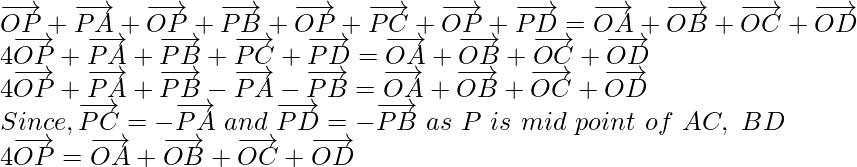
Question 4. Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisect each other.
Solution:

Let us considered ABCD be a quadrilateral and P, Q, R, S be the mid points of sides AB, BC, CD and DA.
So, the position vector of A, B, C and D be 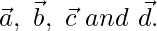
Using the mid point formula
Position vector of P = 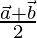
Position vector of Q = 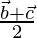
Position vector of R = 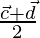
Position vector of S = 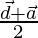
Position vector of 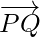 = Position vector of Q – Position vector of P
= Position vector of Q – Position vector of P
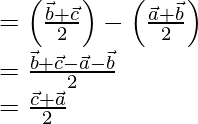 -(1)
-(1)
Position vector of 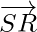 = Position vector of R – Position vector of S
= Position vector of R – Position vector of S
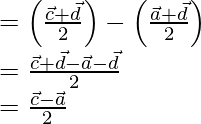 -(2)
-(2)
From eq(1) and (2),
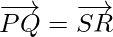
So, PQRS is a parallelogram and PR bisects QS -(as diagonals of parallelogram)
Hence, proved that the line segments joining the mid-points of
opposite sides of a quadrilateral bisect each other.
Question 5. ABCD are four points in a plane and Q is the point of intersection of the lines joining the mid-points of AB and CD; BC and AD. Show that 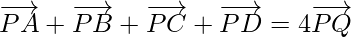 where P is any point.
where P is any point.
Solution:

Let us considered the position vector of the points A, B, C and D are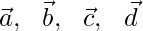
Using the mid-point formula, we get
Position vector of AB = 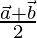
Position vector of BC = 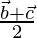
Position vector of CD = 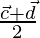
Position vector of DA = 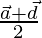
It is given that Q is the mid point of the line joining the mid points of AB and CD, so
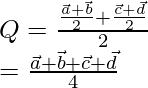
Now, let us assume 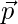 be the position vector of P.
be the position vector of P.
So,
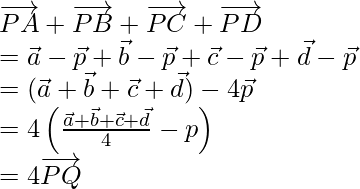
Hence proved
Question 6. Prove by vector method that the internal bisectors of the angles of a triangle are concurrent.
Solution:

In triangle ABC, let us assume that the position vectors of the vertices of the triangle are 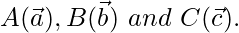
Length of the sides:
BC = x
AC = y
AB = z
In triangle ABC, the internal bisector divides the opposite side in the ratio of the sides containing the angles.
Since AD is the internal bisector of the ∠ABC, so
BD/DC = AB/AC = z/y -(1)
Therefore, position vector of D = 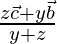
Let the internal bisector intersect at point I.
ID/AI = BD/AB -(2)
BD/DC = z/y
Therefore,
CD/BD = z/y
(CD + BD)/BD = (y + z)/z
BC/BD = (y + z)/z
BD = ln/y + z -(3)
So, from eq(2) and (3), we get
ID/AI = ln/(y +z)
Therefore,
Position vector of I = 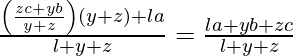
Similarly, we can also prove that I lie on the internal bisectors of ∠B and ∠C.
Hence, the bisectors are concurrent.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...