Class 12 RD Sharma Solutions – Chapter 29 The Plane – Exercise 29.1
Last Updated :
25 Feb, 2021
Question 1(i). Find the equation of the plane passing through the following points (2, 1, 0), (3, -2, -2), and(3, 1, 7).
Solution:
Given points are (2, 1, 0), (3, -2, -2), and (3, 1, 7)
The equation of plane passing through three points is given by
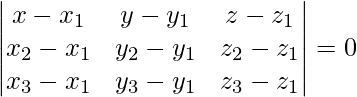
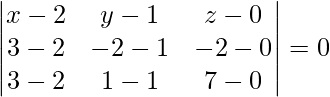
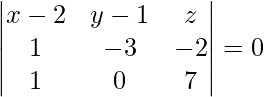
= (x – 2)(-21 – 0) – (y – 1)(7 + 2) + z(0 + 3) = 0
= -21x + 42 – 9y + 9 + 3z = 0
= -21x – 9y + 3z + 51 = 0
By taking -3 as common, we get resultant equation of plane
7x + 3y – z – 17 = 0
Question 1(ii). Find the equation of the plane passing through the following points (-5, 0, 6), (-3, 10, -9) and (-2, 6, -6).
Solution:
Given points are (-5, 0, 6), (-3, 10, -9) and (-2, 6, -6).
The equation of a plane passing through three points is given by
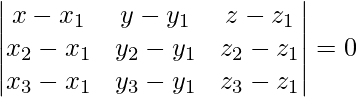
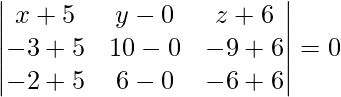
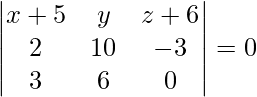
(x + 5)(0 + 18) – y(0 + 9) + (z + 6)(12 – 30) = 0
(x + 5)(18) – y(9) + (z + 6)(-18) = 0
18x + 90 – 9y – 18z -108 = 0
Taking 9 as common, we get equation
2x – y – 2z – 2 = 0
Question 1(iii). Find the equation of the plane passing through the following points (1, 1, 1), (1, -1, 2), and (-2, -2, 2).
Solution:
Given three points are (1, 1, 1), (1, -1, 2), and (-2, -2, 2)
The equation of plane passing through three points is given by
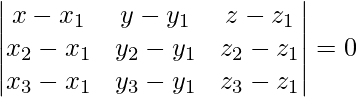
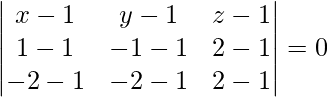
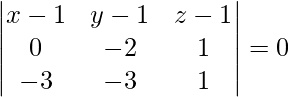
(x – 1)(-2 + 3) – (y – 1)(0 + 3) + (z – 1)(0 – 6) = 0
(x – 1)(1) – (y – 1)(3) + (z – 1)(-6) = 0
x – 1 – 3y + 3 – 6z + 6 = 0
x -3y – 6z + 8 = 0
Question 1(iv). Find the equation of the plane passing through the following points (2, 3, 4), (-3, 5, 1), and (4, -1, 2).
Solution:
Given points are (2, 3, 4), (-3, 5, 1), and (4, -1, 2).
The equation of plane passing through three points is given by
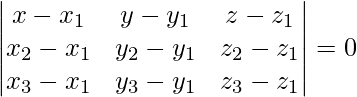
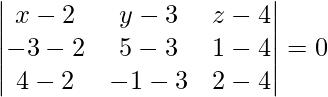
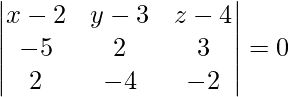
(x – 2)(-4 – 12) – (y – 3)(10 + 6) + (z – 4)(20 – 4) = 0
(x – 2)(-16) – (y – 3)(16) + (z – 4)(16) = 0
-16x – 32 – 16y + 48 + 16z – 64 = 0
-16x – 16y + 16z + 16 = 0
Taking -16 common we get equation of plane as,
x + y – z – 1 = 0
Question 1(v). Find the equation of the plane passing through the following points (0, -1, 0), (3, 3, 0), and (1, 1, 1).
Solution:
Given points are (0, -1, 0), (3, 3, 0), and (1, 1, 1)
The equation of plane passing through three points is given by,
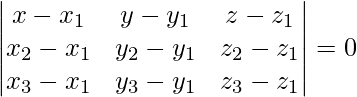
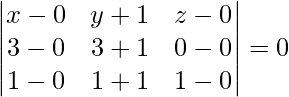
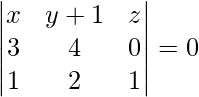
x(4 – 0) – (y + 1)(3 – 0) + z(6 – 4) = 0
4x – (y + 1)(3) + z(2) = 0
4x – 3y – 3 + 2z = 0
4x – 3y + 2z – 3 = 0
Question 2. Show that the four points (0, -1, 1), (4, 5, 1), (3, 9, 4), and (-4, 4, 4) are coplanar and find the equation of the common plane.
Solution:
To prove the given points (0, -1, 1), (4, 5, 1), (3, 9, 4), and (-4, 4, 4) are coplanar.
Efficient solution is to find the equation of plane passing through any three points.
Then substitute the fourth point in the resultant equation.
If it satisfies then the four points are coplanar.
Equation of plane passing through three points (0, -1, 1), (4, 5, 1), and (3, 9, 4) is given by
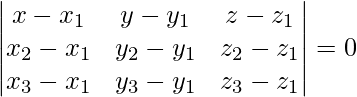
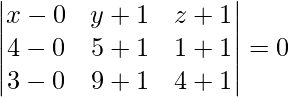
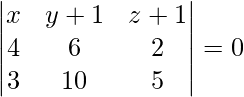
x(30 – 20) – (y + 1)(20 – 6) + (z + 1)(40 – 18) = 0
10x – (y + 1)(14) + (z + 1)(22) = 0
10x – 14y + 22z + 8 = 0
Taking 2 as common,
5x – 7y + 11z + 4 = 0 -Equation (1)
Substitute remaining point (-4, 4, 4) in above eq (1)
5(-4) – 7(4) + 11(4) + 4 = 0
-48 + 48 = 0
0 = 0
LHS = RHS
As the point satisfies the equation. So, the four points are coplanar.
Common plane equation is 5x – 7y + 11z + 4 = 0
Question 3(i). Show that the following points are coplanar (0, -1, 0), (2, 1, -1), (1, 1, 1), and(3, 3, 0).
Solution:
Given points are (0, -1, 0), (2, 1, -1), (1, 1, 1), and(3, 3, 0).
Equation of plane passing through three points (0, -1, 0), (2, 1, -1), (1, 1, 1) is given by
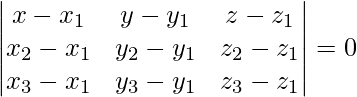
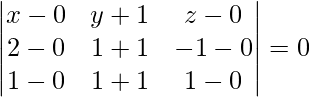
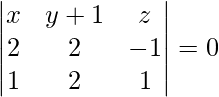
x(2 + 2) – (y + 1)(2 + 1) + z(4 – 2) = 0
x(4) – (y + 1)(3) + z(2) = 0
4x – 3y – 3 + 2z = 0
4x – 3y + 2z – 3 = 0 -Equation (1)
Substitute point four in equation (1)
4(3) – 3(3) + 2 (0) – 3 = 0
12 – 9 + 0 – 3 = 0
12 – 12 = 0
0 = 0
LHS = RHS
As fourth point satisfies the equation.
So, the four points are coplanar
Question 3(ii). Show that the following points are coplanar (0, 4, 3), (-1, -5, -3), (-2, -2, 1), and (1, 1, -1).
Solution:
Given four points are (0, 4, 3), (-1, -5, -3), (-2, -2, 1), and (1, 1, -1).
Equation of points passing through three points is given by
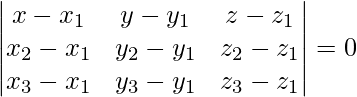
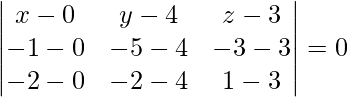
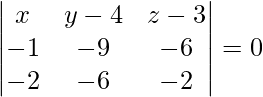
x(18 – 36) – (y – 4)(2 – 12) + (z – 3)(6 – 18) = 0
x(-18) – (y – 4)(-10) + (z – 3)(-12) = 0
-18x + 10y – 40 – 12z + 36 = 0
-18x + 10y – 12z – 4 = 0 -Equation (1)
Substitute fourth point in equation (1)
-18(1) + 10(1) – 12(-1) – 4 = 0
-18 +10 +12 -4 = 0
-22 + 22 = 0
0 = 0
LHS = RHS
As the fourth point satisfies the given equation.
So, the four points are coplanar.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...