Class 12 RD Sharma Solutions – Chapter 22 Differential Equations – Exercise 22.3 | Set 1

Question 1: Show that y=be^x+ce^2x is the solution of the differential equation.

d² y/dx²-3(dy/dx)+2y=0

Solution:

y=be^x+ce^2x (i)

Differentiating equation (i)w.r.t x,

dy/dx=be^x +2ce^2x

dy/dx=be^x+2ce^2x (ii)

Again, differentiating equation (ii)w.r.t x,

d²y/dx² =be^x+4ce^2x (iii)

we have,

d²y/dx² -3(dy/dx)+2y=0 (iv)

Putting the values ofd² y/dx² anddy/dx in equation (iv)

=be^x+4ce^2x-3(be^2x+2ce^2x)+2(be^x+ce^2x)

=3be^x-3be^x+6ce^2x-6ce^2x

=0

So,d²y/dx²-3(dy/dx)+2y=0

Question 2: Verify that y=4sin3x is a solution of the differential equation.

d²y/dx²+9y=0 

Solution:

y=4sin3x (i)

Differentiating equation (i)w.r.t x,

dy/dx=(4)(3)cos3x (ii)

Again differentiating equation (ii)w.r.t x,

d²y/dx² =-(12)(3)sin3x

d²y/dx²=-(9)(4sin3x)

d²y/dx²=-9y (Since y=4sin3x)

d²y/dx2+9y=0

So, d²y/dx²+9y=0

Question 3: Show that y=ae^2x+be^−x is a solution of the differential equation.

d²y/dx²-dy/dx-2y=0

Solution:

y=ae^2x+be^−x (i)

Differentiating equation (i)w.r.t x,

dy/dx=2ae^2x-be^-x (ii)

Again differentiating equation (ii)w.r.t x,

d²y/dx²=4ae^2x+be^-x (iii)

we have,

d²y/dx²-dy/dx-2y (iv)

Putting the values of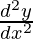andin equation (iv)

=4ae^2x+be^-x-(2ae^2x-be^-x)-2(ae^2x+be^−x)

=4ae^2x-4ae^2x +be^−x-be^−x)

=0

Question 4: Show that the function, y=Acosx-Bsinx is a solution of the differential equation.

d²y/dx²+y=0

Solution:

y=Acosx-Bsinx (i)

Differentiating equation (i)w.r.t x,

dy/dx=-Asinx-Bcosx (ii)

Again differentiating equation (ii)w.r.t x,

d²y/dx²=-Acosx+Bsinx

d²y/dx²=-(Acosx-Bsinx)

d²y/dx²+(Acosx-Bsinx)=0

d²y/dx²+y=0 (since y=Acosx-Bsinx)

Question 5: Show that the function, y=Acos2x-Bsin2x is a solution of the differential equation.

d²y/dx² + 4y = 0

Solution:

y=Acos2x-Bsin2x (i)

Differentiating equation (i)w.r.t x,

dy/dx=-2Asin2x-2Bcos2x (ii)

Again differentiating equation (ii)w.r.t x,

d²y/dx²=-4Acos2x+4Bsin2x

d²y/dx²+4(Acos2x-Bsin2x)=0

d²y/dx²+4y=0 (since y=Acos2x-Bsin2x)

Question 6: Show that, y=Ae^Bx is the solution of the differential equation.

d²y/dx²=(1/y)(dy/dx)²

Solution:

y=Ae^Bx (i)

Differentiating equation (i)w.r.t x,

dy/dx=ABe^Bx (ii)

Again differentiating equation (ii)w.r.t x,

d²y/dx²=AB²e^bx

d²y/dx²=(ABe^bx)² /(Ae^Bx)

d2y/dx2=(1/y)(dy/dx)²

Question 7: Verify that y= (x/a)+b is the solution of the differential equation.

d²y/dx²+(2/x)(dy/dx)²=0

Solution:

y= (x/a)+b (i)

Differentiating equation (i)w.r.t x,

dy/dx=-(a/x²) (ii)

Again differentiating equation (ii)w.r.t x,

d²y/dx²=+(2a/x³)

d²y/dx²=-(-2/x)(a/x²)

d²y/dx²+(2/x)(dy/dx)=0

Question 8: Verify that y²=4ax is the solution of the differential equation.

x(dy/dx)+y(dx/dy)=y

Solution:

y²=4ax (i)

Differentiating equation (i)w.r.t x,

2y(dy/dx)=4a

dy/dx=(2a/y)

we have,

x(dy/dx)+y(dx/dy)

=x(2a/y)+y(y/2a)

=(4xa+y²)/2y

=(2y²/2y)

=y

Question 9: Show that Ax²+By²=1 is the solution of the differential equation.

Solution:

Ax²+By²=1 (i)

Differentiating equation (i)w.r.t x,

2Ax+2By(dy/dx)=0

2Ax=-2By(dy/dx)

y(dy/dx)=-(Ax/B) (ii)

Again differentiating equation (ii)w.r.t x,

(dy/dx)²+y(d²y/dx²)=-(A/B)

(dy/dx)²+y(d²y/dx²)=-(y/x)(dy/dx)

Question 10: Show that y=ax³+bx²+cis the solution of the differential equation.

(d³y/dx³)=6a

Solution:

We have,

y=ax³+bx²+c (i)

Differentiating equation (i)w.r.t x,

(dy/dx)=3ax²+2bx (ii)

Again differentiating equation (ii)w.r.t x,

(d²y/dx²)=6ax (iii)

Again differentiating equation (iii)w.r.t x,

(d³y/dx³)=6a