Question 1: If a matrix has 8 elements, what are the possible orders it can have? What if it has 5 elements?
Solution:
Part 1:
Let the matrix be of mxn dimension.
Hence, mxn = 8.
Then, all we have to do is, find the divisors of 8, which are : 1, 2, 4, 8.
Thus, the possible orders are: 1×8, 8×1, 2×4 and 4×2.
Part 2:
Following a similar approach:
Since, mxn = 5.
The divisors of 5 are : 1,5.
Thus, the possible orders are: 1×5 and 5×1.
Question 2(i): If A = [aij] = 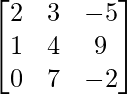 and B = [bjj] =
and B = [bjj] = 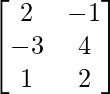 then find a22+b21.
then find a22+b21.
Solution:
We know that every element in a matrix A of dimensions mxn can be addressed as aij, where 1≤ i ≤ m and 1 ≤ j ≤ n.
Thus, a22 is the 2nd element in the 2nd row of A, and b21 is the 1rst element in the 2nd row of B.
That implies, a22 + b21 = 4 + (-3) = 1.
Question 2(ii): If A = [aij]= 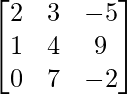 and B = [bij] =
and B = [bij] = 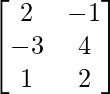 then find a11b11 + a22b22.
then find a11b11 + a22b22.
Solution:
As seen in the previous question, every element in a matrix A of dimensions mxn can be addressed as aij, where 1≤ i ≤ m and 1 ≤ j ≤ n.
Thus,
a11 = 1rst element in the 1rst row of A = 2.
a22 = 2nd element in the 2nd row of A = 4.
b11 = 1rst element in the 1rst row of B = 2.
b22 = 2nd element in the 2nd row of B = 4.
That implies, a11b11 + a22b22 = (2×2) + (4×4) = 4 + 16 = 20.
Question 3: Let A be a matrix of order 3×4. If R1 denotes the first row of A and C2 denotes its second column, then determine the orders of matrices R1 and C2.
Solution:
Given, A is a matrix of order 3×4.
We know that a matrix having an order of mxn has m rows and n columns.
Thus, A contains, 3 rows, and each row contains 4 elements.
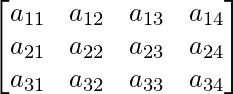
Now, if R1 is a row, it has 4 elements, and thus its order can be written as 1×4, 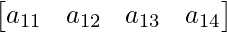
And similarly, if C2 is a column, it will have 3 rows, each with 1 element, and thus its order is 3×1, 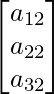
Question 4(i): Construct a 2×3 matrix A = [aij] whose elements aij are given by : aij = i x j.
Solution:
We know that A is a matrix of order 2×3.
Thus A can be depicted as: 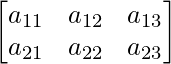
Since each element is a product of its row number and column number (i x j):
a11 = 1 a12 = 2 a13 = 3
a21 = 2 a22 = 4 a23 = 6
Thus, A can be depicted as : 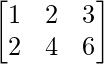
Question 4(ii): Construct a 2×3 matrix A = [aij] whose elements aij are given by : aij = 2i – j.
Solution:
We know that A is a matrix of order 2×3.
Thus A can be depicted as: 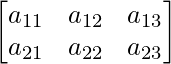
Since each element can be defined as (2 x (row number)) – column number:
a11 = 1 a12 = 0 a13 = -1
a21 = 3 a22 = 2 a23 = 1
Thus, A can be depicted as : 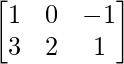
Question 4(iii): Construct a 2×3 matrix A = [aij] whose elements aij are given by : aij = i + j.
Solution:
We know that A is a matrix of order 2×3.
Thus A can be depicted as: 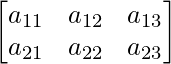
Since each element can be defined as the sum of its row number and column number:
a11 = 2 a12 = 3 a13 = 4
a21 = 3 a22 = 4 a23 = 5
Thus, A can be depicted as : 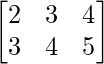
Question 4(iv): Construct a 2×3 matrix A = [aij] whose elements aij are given by : aij = 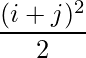 .
.
Solution:
We know that A is a matrix of order 2×3.
Thus A can be depicted as: 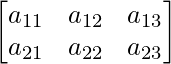
Since each element can be defined as : 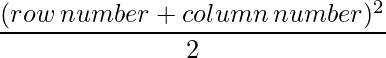 ,
,
a11 = 2 a12 = 4.5 a13 = 8
a21 = 4.5 a22 = 8 a23 = 12.5
Thus, A can be depicted as : 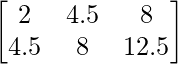
Question 5(i): Construct a 2×2 matrix A = [aij] whose aij are given by : 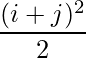 .
.
Solution:
We know that A is a matrix of order 2×2.
Thus A can be depicted as : 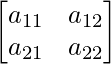
Since each element can be defined as :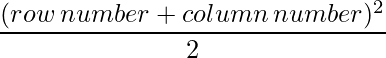 ,
,
a11 = 2 a12 = 4.5
a21 = 4.5 a22 = 8
Thus, A can be depicted as : 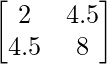
Question 5(ii): Construct a 2×2 matrix A = [aij] whose aij are given by : 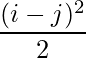 .
.
Solution:
We know that A is a matrix of order 2×2.
Thus A can be depicted as : 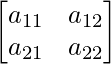
Since each element can be defined as : 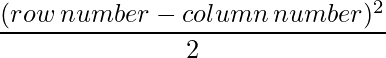 ,
,
a11 = 0 a12 = 0.5
a21 = 0.5 a22 = 0
Thus, A can be depicted as : 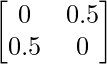
Question 5(iii): Construct a 2×2 matrix A = [aij] whose aij are given by : 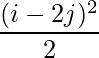 .
.
Solution:
We know that A is a matrix of order 2×2.
Thus A can be depicted as : 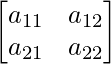
Since each element can be defined as : 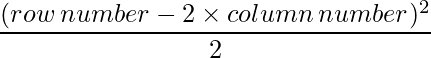 ,
,
a11 = 0.5 a12 = 4.5
a21 = 0 a22 = 2
Thus, A can be depicted as : 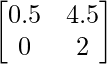
Question 5(iv): Construct a 2×2 matrix A = [aij] whose aij are given by : 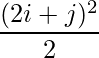 .
.
Solution:
We know that A is a matrix of order 2×2.
Thus A can be depicted as : 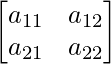
Since each element can be defined as : 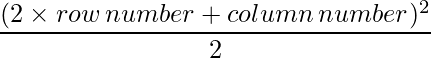 ,
,
a11 = 4.5 a12 = 8
a21 = 12.5 a22 = 18
Thus, A can be depicted as : 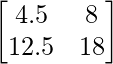
Question 5(v): Construct a 2×2 matrix A = [aij] whose aij are given by : 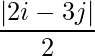 .
.
Solution:
We know that A is a matrix of order 2×2.
Thus A can be depicted as : 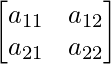 ,
,
Since each element can be defined as : 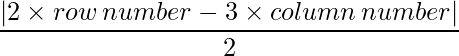 ,
,
a11 = 0.5 a12 = 2
a21 = 0.5 a22 = 1
Thus, A can be depicted as : 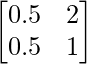
Question 5(vi): Construct a 2×2 matrix A = [aij] whose aij are given by : 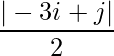 .
.
Solution:
We know that A is a matrix of order 2×2.
Thus A can be depicted as : 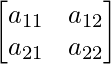 ,
,
Since each element can be defined as : 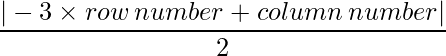 ,
,
a11 = 1 a12 = 0.5
a21 = 2.5 a22 = 2
Thus, A can be depicted as : 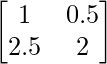
Question 5(vii) Construct a 2×2 matrix A = [aij] whose aij are given by : 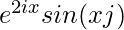 .
.
Solution:
We know that A is a matrix of order 2×2.
Thus A can be depicted as : 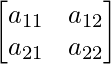 ,
,
Since each element can be defined as : 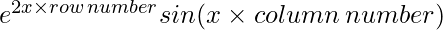 ,
,
a11 = e2xsinx a12 = e2xsin2x
a21 = e4xsinx a22 = e4xsin2x
Thus, A can be depicted as : 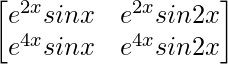
Question 6(i): Construct a 3×4 matrix A = [aij] whose aij are given by : aij = i + j .
Solution:
A is a matrix of order 3×4.
Thus, A can be depicted as : 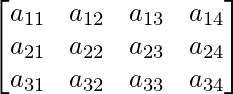 ,
,
Since each element can be defined as : ( row number + column number ),
a11 = 2 a12 = 3 a13 = 4 a14 = 5
a21 = 3 a22 = 4 a23 = 5 a24 = 6
a31 = 4 a32 = 5 a33 = 6 a34 = 7
Thus, A can be depicted as : 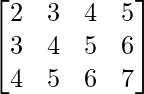
Question 6(ii): Construct a 3×4 matrix A = [aij] whose aij are given by : aij = i – j.
Solution:
A is a matrix of order 3×4.
Thus, A can be depicted as : 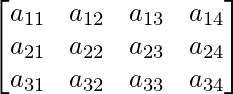 ,
,
Since each element can be defined as : (row number – column number),
a11 = 0 a12 = -1 a13 = -2 a14 = -3
a21 = 1 a22 = 0 a23 = -1 a24 = -2
a31 = 2 a32 = 1 a33 = 0 a34 = -1
Thus, A can be depicted as : 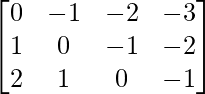
Question 6(iii): Construct a 3×4 matrix A = [aij] whose aij are given by : aij = 2i .
Solution:
A is a matrix of order 3×4.
Thus, A can be depicted as : 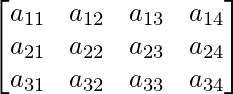 ,
,
Since each element can be defined as : (2 x row number ),
a11 = 2 a12 = 2 a13 = 2 a14 = 2
a21 = 4 a22 = 4 a23 = 4 a24 = 4
a31 = 6 a32 = 6 a33 = 6 a34 = 6
Thus, A can be depicted as : 
Question 6(iv): Construct a 3×4 matrix A = [aij] whose aij are given by : aij = j.
Solution:
A is a matrix of order 3×4.
Thus, A can be depicted as : 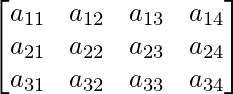 ,
,
Since each element can be defined as : (column number ),
a11 = 1 a12 = 2 a13 = 3 a14 = 4
a21 = 1 a22 = 2 a23 = 3 a24 = 4
a31 = 1 a32 = 2 a33 = 3 a34 = 4
Thus, A can be depicted as : 
Question 6(v): Construct a 3×4 matrix A = [aij] whose aij are given by : aij = 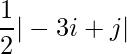 .
.
Solution:
A is a matrix of order 3×4.
Thus, A can be depicted as : 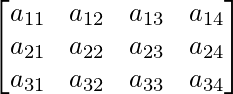 ,
,
Since each element can be defined as :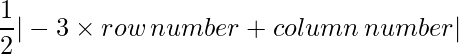 ,
,
a11 = -1 a12 = -1/2 a13 = 0 a14 = 1/2
a21 = -5/2 a22 = -2 a23 = -3/2 a24 = -1
a31 = -4 a32 = -7/2 a33 = -3 a34 = -5/2
Thus, A can be depicted as : 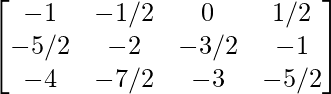
Question 7(i): Construct a 4×3 matrix A = [aij] whose aij are given by : aij = 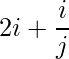 .
.
Solution:
A is a matrix of order 4×3.
Thus, A can be depicted as : 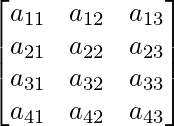
Since each element can be defined as : 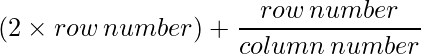 ,
,
a11 = 3 a12 = 5/2 a13 = 7/3
a21 = 6 a22 = 5 a23 = 14/3
a31 = 9 a32 = 15/2 a33 = 7
a41 = 12 a42 = 10 a43 = 28/3
Thus, A can be depicted as : 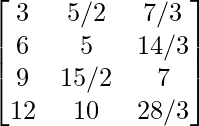
Question 7(ii): Construct a 4×3 matrix A = [aij] whose aij are given by : aij = 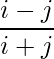 .
.
Solution:
A is a matrix of order 4×3.
Thus, A can be depicted as: 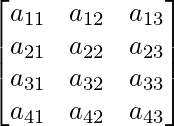
Since each element can be defined as : 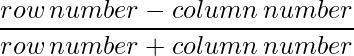 ,
,
a11 = 0 a12 = -1/3 a13 = -1/2
a21 = 1/3 a22 = 0 a23 = -1/5
a31 = 1/2 a32 = 1/5 a33 = 0
a41 = 3/5 a42 = 1/3 a43 = 1/7
Thus, A can be depicted as : 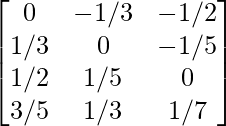
Question 7(iii): Construct a 4×3 matrix A = [aij] whose aij are given by : aij = i.
Solution:
A is a matrix of order 4×3.
Thus, A can be depicted as : 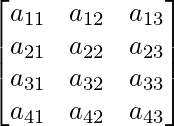
Since each element can be defined as : (row number)
a11 = 1 a12 = 1 a13 = 1
a21 = 2 a22 = 2 a23 = 2
a31 = 3 a32 = 3 a33 = 3
a41 = 4 a42 = 4 a43 = 4
Thus, A can be depicted as : 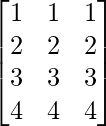
Question 8: Find x, y, a and b if: 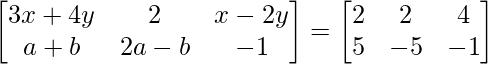
Solution:
We can see that both, the matrix on the Left Hand Side (LHS) and the matrix on the Right Hand Side (RHS are of the dimension 2×3.
Since, the matrix on LHS is equal to the matrix on the RHS, each element on the LHS at the index (i, j) must be equal to each element on the RHS at the index (i, j).
Hence, equating each element on RHS to LHS:
a11: 3x+4y = 2 ………………(eq.1) a12: 2 = 2 a13: x-2y = 4 ………………(eq.2)
a21: a+b = 5 ………………(eq.3) a22: 2a-b = -5……………..(eq.4) a23: -1 = -1
Thus, (eq.1) and (eq.2) form one system of equations comprising variables x and y.
Solving (eq.1) and (eq.2): (eq.1) + 2x(eq.2)
=> (3x+2x) + (4y-2(2y)) = 2+ (2(4))
=> 5x = 10
=> x = 2
Substituting (x=2) in (eq.1) :
=> (3(2)) + 4y = 2
=> 4y = 2-6 = -4
=> y=-1
Similarly, (eq.3) and (eq.4) form a system of equations comprising variables a and b.
Solving (eq.3) and (eq.4) : (eq.1) + (eq.2)
=> (a+2a) + (b-b) = 5 – 5
=> 3a = 0
=> a = 0
Substituting (a=0) in (eq.3):
=> 0 + b = 5
=>b = 5
Thus, a=0, b=5, x=2 and y=-1.
Question 9: Find x, y, a and b if : 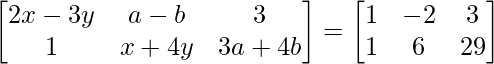 .
.
Solution:
We can see that both, the matrix on the Left Hand Side (LHS) and the matrix on the Right Hand Side (RHS are of the dimension 2×3.
Since, the matrix on LHS is equal to the matrix on the RHS, each element on the LHS at the index (i, j) must be equal to each element on theRHS at the index (i, j).
Hence, equating each element on RHS to LHS:
a11 : 2x-3y = 1………………(eq.1) a12 : a-b = -2………………(eq.2) a13 : 3 = 3
a21 : 1 = 1 a22 : x+4y = 6……………..(eq.3) a23 : 3a+4b = 29………………(eq.4)
Thus, (eq.1) and (eq.3) form one system of equations comprising of variables x and y.
Solving (eq.1) and (eq.2) : (eq.1) – 2x(eq.2)
=> (2x-2x) + (-3y-2(4y)) = 1- (2(6))
=> -11y = -11
=> y = 1
Substituting (y=1) in (eq.1) :
=> 2x – 3(1) = 1
=> 2x = 3+1 = 4
=> x = 2
Similarly, (eq.2) and (eq.4) form a system of equations comprising of variables a and b.
Solving (eq.2) and (eq.4) : 4x(eq.1) + (eq.2)
=> (4a+3a) + (-4(b)+4b) = 4(-2) + 29
=> 7a = 21
=> a = 3
Substituting (a=3) in (eq.2) :
=> 3 – b = -2
=>b = 5
Thus, a=3, b=5, x=2 and y=1.
Question 10: Find a, b, c and d if : 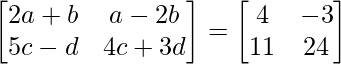
Solution:
We can see that both, the matrix on the Left Hand Side (LHS) and the matrix on the Right Hand Side (RHS are of the dimension 2×2.
Since, the matrix on LHS is equal to the matrix on the RHS, each element on the LHS at the index (i, j) must be equal to each element on the RHS at the index (i, j).
Hence, equating each element on RHS to LHS:
a11 : 2a+b = 4 ………….(eq.1)
a12 : a-2b = -3 …………(eq.2)
a21 : 5c-d = 11 …………(eq.3)
a22 : 4c+3d = 24 ……..(eq.4)
Thus, (eq.1) and (eq.2) form one system of equations comprising of variables a and b.
Solving (eq.1) and (eq.2) : (eq.1) – 2x(eq.2)
=> (2a-2a) + (b+4b) = 4 + (-2(-3))
=> 5b = 10
=> b = 2
Substituting (b=2) in (eq.1) :
=> 2a + 2 = 4
=> 2a = 4-2 = 2
=> a=1
Similarly, (eq.3) and (eq.4) form a system of equations comprising of variables c and d.
Solving (eq.3) and (eq.4) : 3x(eq.1) + (eq.2)
=> (15c+4c) + (-3d+3d) = 33 + 24
=> 19c = 57
=> c = 3
Substituting (c=3) in (eq.4) :
=> (4(3)) + 3d = 24
=>3d = 24 – 12 = 12
=>d = 4
Thus, a=1, b=2, c=3 and d=4.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...