Class 12 RD Sharma Solutions – Chapter 22 Differential Equations – Exercise 22.5 | Set 2
Last Updated :
21 Feb, 2021
Question 14. sin4x(dy/dx) = cosx
Solution:
We have,
sin4x(dy/dx) = cosx
dy = (cosx/sin4x)dx
Let, sinx = z
On differentiating both sides, we get
cosx dx = dz
dy = (dz/z4)
On integrating both sides, we get
∫(dy) = ∫(1/z4)dz
y = (1/ -3t3) + c
y = -(1/3sin3x) + c
y = (-cosec3x/3) + c -(Here, ‘c’ is integration constant)
Question 15. cosx(dy/dx) – cos2x = cos3x
Solution:
We have,
cosx(dy/dx) – cos2x = cos3x
(dy/dx) = (cos3x + cos2x)/cosx
(dy/dx) = (4cos3x – 3cosx + 2cos2x – 1)/cosx
(dy/dx) = (4cos3x/cosx) – 3(cosx/cosx) + 2(cos2x/cosx) – secx
dy = [4cos2x – 3 + 2cosx – secx]dx
dy = [4{(cos2x + 1)/2} – 3 + 2cosx – secx]dx
On integrating both sides, we get
∫dy = ∫[2cos2x – 1 + 2cosx – secx]dx
y = sin2x – x + 2sinx – log|secx + tanx| + c -(Here, ‘c’ is integration constant)
Question 16. √(1 – x4)(dy/dx) = xdx
Solution:
We have,
√(1 – x4)(dy/dx) = xdx
Let, x2 = z
On differentiating both sides, we get
2xdx = dz
xdx = (dz/2)
√(1 – z2)dy = (dz/2)
dy = 
On integrating both sides, we get
∫dy = ∫
y = (1/2)sin-1(z) + c
y = (1/2)sin-1(x2) + c -(Here, ‘c’ is integration constant)
Question 17. √(a + x)(dy) + xdx = 0
Solution:
We have,
√(a + x)(dy) + xdx = 0
dy =  dx
dx
Let, (x + a) = z2
On differentiating both sides, we get
dx = 2zdz
(x + a) = z2
x = z2 – a
dy = -2[(z2 – a)/z]zdz
On integrating both sides, we get
∫dy = -2∫[(z2 – a)/z]zdz
y = -(2/3)(z3) + 2az + c
y = -(2/3)(x + a)3/2 + 2a√(x + a) + c -(Here, ‘c’ is integration constant)
Question 18. (1 + x2)(dy/dx) – x = 2tan-1x
Solution:
We have,
(1 + x2)(dy/dx) – x = 2tan-1x
(1 + x2)(dy/dx) = 2tan-1x + x
dy/dx = 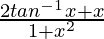
dy 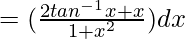
On integrating both sides, we get
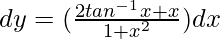
y = I1 + I2
I1 = ∫(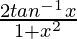
Let, tan-1x = z
On differentiating both sides, we get
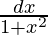 = dz
= dz
= ∫2zdx
= z2
I1 = (tan-1x)2
I2 = ∫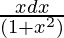
= (1/2)log|1 + x2|
y = (tan-1x)2 + 1/2log|1 + x2|+ c -(Here, ‘c’ is integration constant)
Question 19. (dy/dx) = xlogx
Solution:
We have,
(dy/dx) = xlogx
dy = xlogxdx
On integrating both sides, we get
∫dy = ∫xlogxdx
y = log|x|∫xdx – ∫[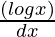 ∫xdx]dx
∫xdx]dx
y = (x2/2)log|x| – ∫(1/x)(x2/2)dx
y = (x2/2)log|x| – ∫(x/2)dx
y = (x2/2)log|x| – (x2/4) + c -(Here, ‘c’ is integration constant)
Question 20. (dy/dx) = xex – (5/2) + cos2x
Solution:
We have,
(dy/dx) = xex – (5/2) + cos2x
dy = (xex – (5/2) + cos2x) dx
On integrating both sides, we get
∫dy = ∫xex dx – 5/2∫dx + ∫cos2x dx
y = ∫xex dx – 5/2∫dx + ∫(1 + cos2x)/2 dx
= ∫xex dx – 5/2∫dx + 1/2∫dx + 1/2∫cos2x dx
= ∫xex dx – 2∫dx + 1/2∫cos2x dx
= x∫ex dx – ∫(1∫ex dx)dx – 2x + sin2x/4 dx
= xex – ex – 2x + 1/4sin2x + c
Question 21. (x3 + x2 + x + 1)(dy/dx) = 2x2 + x
Solution:
We have,
(x3 + x2 + x + 1)(dy/dx) = 2x2 + x
(dy/dx) = (2x2 + x)/(x3 + x2 + x + 1)
dy = 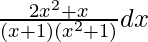
On integrating both sides, we get
∫dy = ∫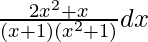
Let,

2x2 + x = Ax2 + A + Bx2 + Bx + Cx + C
2x2 + x = (A + B)x2 + (B + C)x + (A + C)
On comparing the coefficients on both sides,
(A + B) = 2
(B + C) = 1
(A + C) = 0
After solving the equations,
A = (1/2)
B = (3/2)
C = -(1/2)
y = (1/2)∫(dx/(x + 1) + 
y = (1/2)log(x + 1) + (3/4)∫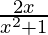 dx – (1/2)∫
dx – (1/2)∫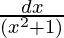
y = (1/2)log|x + 1| + (3/4)log|x2 + 1| – (1/2)tan-1x + c -(Here, ‘c’ is integration constant)
Question 22. sin(dy/dx) = k, y(0) = 1
Solution:
We have,
sin(dy/dx) = k,
(dy/dx) = sin-1(k)
dy = sin-1(k)dx
On integrating both sides, we get
∫dy = sin-1(k)∫dx
y = xsin-1k + c -(1)
Put x = 0, y = 1
1 = 0 + c
1 = c
On putting the value of c in equation(1)
y = xsin-1k + 1
y – 1 = xsin-1x
Question 23. e(dy/dx) = x + 1, y(0) = 3
Solution:
We have,
e(dy/dx) = x + 1
(dy/dx) = log(x + 1)
dy = log(x + 1)dx
On integrating both sides, we get
∫dy = ∫log(x + 1)dx
y = log(x + 1)∫dx – ∫[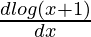 ∫dx]dx
∫dx]dx
y = xlog(x + 1) – ∫[x/(x + 1)]dx
y = xlog(x + 1) – ∫1 - \frac{1}{(x+1)}dx
y = xlog(x + 1) – x + log(x + 1) + c
y = (x + 1)log(x + 1) – x + c -(1)
Put, y = 3, x = 0 in equation(1)
3 = 0 + c
y = (x + 1)log(x + 1) – x + 3
Question 24. c'(x) = 2 + 0.15x, c(0) = 100
Solution:
We have,
c'(x) = 2 + 0.15x -(1)
On integrating both sides, we get
∫c'(x)dx = ∫(2 + 0.15x)dx
c(x) = 2x + 0.15(x2/2) + c -(2)
Put, c(0) = 100, x = 0 in equation(2)
100 = 2(0) + 0 + c
c = 100
c(x) = 2x + 0.15(x2/2) + 100
Question 25. x(dy/dx) + 1 = 0, y(-1) = 0
Solution:
We have,
x(dy/dx) + 1 = 0
xdy = -dx
dy = -(dx/x)
On integrating both sides, we get
∫dy = -∫(dx/x)
y = -logx + c -(1)
Put, y = 0, x = -1 in equation(1)
0 = 0 + c
c = 0
y = -log|x|
Question 26. x(x2 – 1)(dy/dx) = 1, y(2) = 0
Solution:
We have,
x(x2 – 1)(dy/dx) = 1 -(1)
dy = dx/x(x + 1)(x – 1)
On integrating both sides, we get
∫dy = ∫dx/x(x + 1)(x – 1)
Let, 1/x(x + 1)(x – 1) = A/x + B/(x + 1) + C/(x – 1)
1 = A(x + 1)(x – 1) + B(x)(x – 1) + C(x)(x + 1) -(2)
Put, x = 0, -1, 1 respectively and simplify above equation, we get,
A = -1, B = (1/2), C = (1/2)
y = 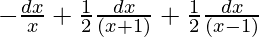
y = -logx + (1/2)log(x + 1) + (1/2)log(x – 1)
y = (1/2)log(1/x2) + (1/2)log(x + 1) + (1/2)log(x – 1) + c -(3)
Put, y = 0, x = 2 in equation(3)
0 = (1/2)log(1/4) + (1/2)log(3) + 0 + c
c = -(1/2)log(3/4)
y = (1/2)log[(x2 – 1)/x2] – (1/2)log(3/4)
![Rendered by QuickLaTeX.com y=\frac{1}{2}log[\frac{4}{3}\frac{(x^2-1)}{x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-65ae9ff91b59a299b0720183e319f0c2_l3.png)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...