Skip to content
Related Articles
Open in App
Not now

Related Articles

Class 12 RD Sharma Solutions – Chapter 28 The Straight Line in Space – Exercise 28.1 | Set 1

Improve Article
Save Article
Like Article
  • Last Updated : 04 May, 2021
Improve Article
Save Article
Like Article

Question 1. Find the vector and Cartesian equation of the line through the points (5, 2, -4) and which is parallel to the vector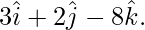3\hat{i}+2\hat{j}-8\hat{k}.

Solution:

As we know that the vector equation of a line is;

\vec{r}=\vec{a}+\lambda\vec{b}

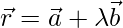
Thus, the Cartesian equation of a line is;

\frac{x-x_1}{a_1}=\frac{y-y_1}{a_2}=\frac{x-x_3}{a_3}

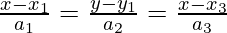
After applying the above formulas;

The vector equation of the line is;

\vec{r}=(5\hat{i}+2\hat{j}-4\hat{k})+\lambda(3\hat{i}+2\hat{j}-8\hat{k})

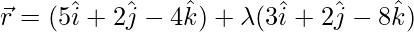
The Cartesian equation of a line is;

\frac{x-5}{3}=\frac{y-2}{2}=\frac{z+4}{-8}

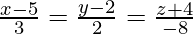
Question 2. Find the vector equation of the line passing through the points (-1, 0, 2) and (3, 4, 6).

Solution:

Given:

Here, the direction ratios of the line are;

(3 + 1, 4 – 0, 6 – 2) = (4, 4, 4)

Thus, the given line passes through

(-1, 0, 2)

As we know that the vector equation of a line is given as;

\vec{r}=\vec{a}+\lambda\vec{b}

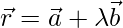
Thus, substitute values

Hence, we get

\vec{r}=\vec{a}+\lambda\vec{b}\\ \vec{r}=(-\vec{i}+0\vec{j}+2\vec{k})+\lambda(4\vec{i}+4\vec{j}+4\vec{k})

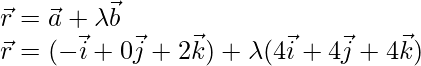
Therefore,

Vector equation of the line is;

\vec{r}=(-\vec{i}+0\vec{j}+2\vec{k})+\lambda(4\vec{i}+4\vec{j}+4\vec{k})

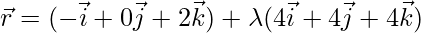
Question 3. Fine the vector equation of a line which is parallel to the vector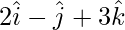2\hat{i}-\hat{j}+3\hat{k} and which passes through the point (5, -2, 4), Also, reduce it to Cartesian form.

Solution:

Consider,

The vector equation of line passing through a fixed point vector a and parallel to vector b is shown as;

\vec{r}=\vec{a}+\lambda\vec{b}

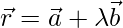
Here, λ is scalar

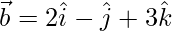\vec{b}=2\hat{i}-\hat{j}+3\hat{k} and\vec{a}=5\hat{i}-2\hat{j}+4\hat{k}

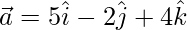
The equation of the required line is;

\vec{r}=\vec{a}+\lambda\vec{b}\\ \vec{r}=(5\hat{i}-2\hat{j}+4\hat{k})+\lambda(2\hat{i}-\hat{j}+3\hat{k})

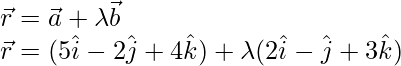
Now substitute the value of r here

\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}

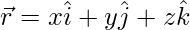
Thus, we get

(x\hat{i}+y\hat{j}+z\hat{k})=(5+2\lambda)\hat{i}+(-2-\lambda)\hat{j}+(4+3\lambda)\hat{k}

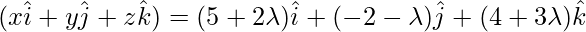
Now compare the coefficients of vector

x = 5 + 2λ,y = -2 – λ,z = 4 + 3λ

After equating to λ,

We will have

\frac{x-5}{2}=λ ,\ \ \frac{y+2}{-0}=λ ,\ \ \frac{z-4}{3}=λ

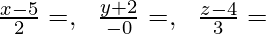
Therefore,

The Cartesian form of equation of the line is;

\frac{x-5}{2} =\ \ \frac{y+2}{-0} =\ \ \frac{z-4}{3}

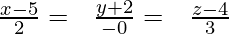
Question 4. A line passing through the point with position vector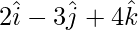2\hat{i}-3\hat{j}+4\hat{k} and is in the direction of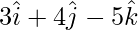3\hat{i}+4\hat{j}-5\hat{k} . Find equations of the line in vector and Cartesian form.

Solution:

Consider,

The vector equation of line passing through a fixed point vector a and parallel to vector b is shown as;

\vec{r}=\vec{a}+\lambda\vec{b}

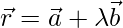
Here, λ is scalar

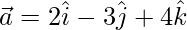\vec{a}=2\hat{i}-3\hat{j}+4\hat{k} and\vec{b}=3\hat{i}+4\hat{j}-5\hat{k}

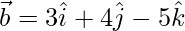
The equation of the required line is;

\vec{r}=\vec{a}+\lambda\vec{b}\\ \vec{r}=(2\hat{i}-3\hat{j}+4\hat{k})+\lambda(3\hat{i}+4\hat{j}-5\hat{k})

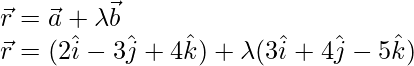
Now substitute the value of r here

\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}

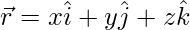
Thus, we get

(x\hat{i}+y\hat{j}+z\hat{k})=(2+3\lambda)\hat{i}+(-3+4\lambda)\hat{j}+(4-5\lambda)\hat{k}

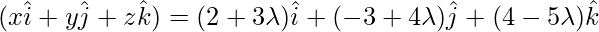
Now compare the coefficients of vector

x = 2 + 3λ,y = -3 + 4λ,z = 4 – 5λ

After equating to λ,

We will have

\frac{x-2}{3}=λ ,\ \ \frac{y+3}{4}=λ ,\ \ \frac{z-4}{-5}=λ

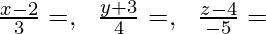
Therefore,

The Cartesian form of equation of the line is;

\frac{x-2}{3} =\ \ \frac{y+3}{4} =\ \ \frac{z-4}{-5}

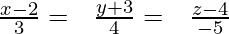
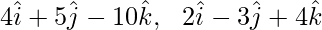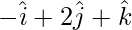Question 5. ABCD is a parallelogram. The position vectors of the points A, B and C are respectively, 4\hat{i}+5\hat{j}-10\hat{k},\ \ 2\hat{i}-3\hat{j}+4\hat{k} and-\hat{i}+2\hat{j}+\hat{k} . Find the vector equation of the line BD. Also reduce it to Cartesian form.

Solution:

Given: ABCD is a parallelogram.

Consider: AC and BD bisects each other at point O.

Thus,

Position vector of point O =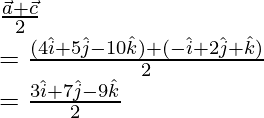\frac{\vec{a}+\vec{c}}{2}\\ =\frac{(4\hat{i}+5\hat{j}-10\hat{k})+(-\hat{i}+2\hat{j}+\hat{k})}{2}\\ =\frac{3\hat{i}+7\hat{j}-9\hat{k}}{2}

Now, Consider position vector of point O and B are represented by

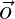\vec{o} and\vec{b}

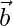
Thus,

Equation of the line BD is the line passing through O and B is given by

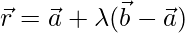\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a}) [Since equation of the line passing through two points\vec{a} and\vec{b} ]

\vec{r}=\vec{a}+\lambda(\vec{o}-\vec{b})\\ (2\hat{i}-3\hat{j}+4\hat{k})+\lambda\left(\frac{3\hat{i}+7\hat{j}-9\hat{k}}{2}-2\hat{i}-3\hat{j}+4\hat{k}\right)\\ \vec{r}=(2\hat{i}-3\hat{j}+4\hat{k})+\lambda(3\hat{i}+7\hat{j}-9\hat{k}-4\hat{i}+6\hat{j}-8\hat{k})\\ \vec{r}=(2\hat{i}-3\hat{j}+4\hat{k})+\lambda(-\hat{i}+13\hat{j}-17\hat{k})

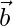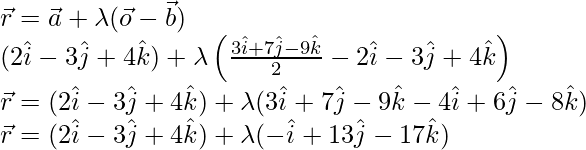
Now, compare the coefficients of vector i, j, R

x = 2 – λ, y = -3 – 13λ, z = 4 – 17λ

After equating to λ,

We will have

\frac{x-2}{-1}=λ ,\ \ \frac{y+3}{13}=λ ,\ \ \frac{z-4}{-17}=λ

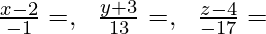
Therefore,

The Cartesian form of equation of the line is;

\frac{x-2}{-1} =\ \ \frac{y+3}{13} =\ \ \frac{z-4}{-17}

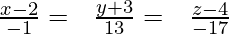
Question 6. Find the vector form as well as in Cartesian form, the equation of line passing through the points A(1, 2, -1) and B(2, 1, 1).

Solution:

We know that, equation of line passing though two points (x1, y1 ,z1) and (x2, y2, z2) is

\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}\ \ \ \ \ \ \ ....(i)\\

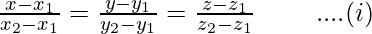
Here,

(x1, y1, z1) = A(1, 2, -1)

(x2, y2 ,z2) = B(2, 1, 1)

Using equation (i), equation of line AB,

\frac{x-1}{2-1}=\frac{y-2}{1-2}=\frac{z+1}{1+1}\\ \frac{x-1}{1}=\frac{y-2}{-1}=\frac{z+1}{2}=\lambda\ (assume)

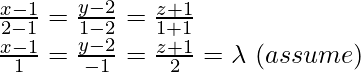
x = λ + 1, y = -λ + 2, z = 2λ – 1

Vector form of equation of line AB is,

x\hat{i}+y\hat{j}+z\hat{k}=(\lambda+1)\hat{i}+(-\lambda+2)\hat{j}+(2\lambda-1)\hat{k}\\ \vec{r}=(\hat{i}+2\hat{j}-\hat{k})+\lambda(\hat{i}-\hat{j}+2\hat{k})

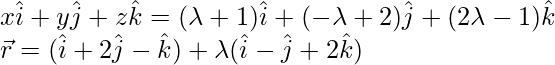
Question 7. Find the vector equation for the line which passes through the point (1, 2, 3) and parallel to the vector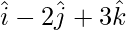\hat{i}-2\hat{j}+3\hat{k}. Reduce the corresponding equation in Cartesian form.

Solution:

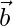We know that vector equation of a line passing through\vec{a} and parallel to the vector\vec{b} is given by,

\vec{r}=\vec{a}+\lambda\vec{b}

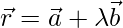
Here,

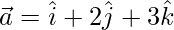\vec{a}=\hat{i}+2\hat{j}+3\hat{k} and\vec{b}=\hat{i}-2\hat{j}+3\hat{k}

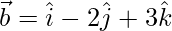
So, required vector equation of line is,

\vec{r}=(\hat{i}+2\hat{j}+3\hat{k})+\lambda(\hat{i}-2\hat{j}+3\hat{k})

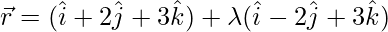
Now,

(x\hat{i}+y\hat{j}+z\hat{k})=(1+\lambda)\hat{i}+(2-2\lambda)\hat{j}+(3+3\lambda)\hat{k}

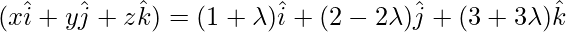
Equating the coefficients of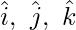\hat{i},\ \hat{j},\ \hat{k}

x = 1 + λ, y = 2 – 2λ, z = 3 + 3λ

x – 1 = λ,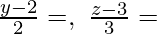\frac{y-2}{2}=λ,\ \frac{z-3}{3}=λ

So, required equation of line is Cartesian form,

\frac{x-1}{1}=\frac{y-2}{-2}=\frac{z-3}{3}

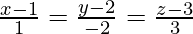
Question 8. Find the vector equation of a line passing through (2, −1, 1) and parallel to the line whose equations are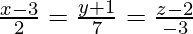\frac{x-3}{2}=\frac{y+1}{7}=\frac{z-2}{-3}

Solution:

We know that, equation of a line passing through a point (x1, y1, z1) and having direction ratios proportional to a, b, c is

\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\ \ \ \ .....(i)

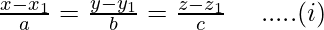
Here,

(x1, y1, z1) = (2, -1, 1) and

Given line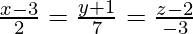\frac{x-3}{2}=\frac{y+1}{7}=\frac{z-2}{-3} is parallel to required line.

a = 2μ, b = 7μ, c = -3μ

So, equation of required line using equation (i)

\frac{x-2}{2μ }=\frac{y+1}{7μ }=\frac{z-1}{-3μ }\\ \frac{x-2}{2}=\frac{y+1}{7}=\frac{z-1}{-3}=\lambda

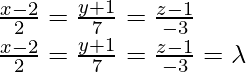
x = 2λ + 2, y = 7λ – 1, z = -3λ + 1

So,

x\hat{i}+y\hat{j}+z\hat{k}=(2λ+2)\hat{i}+(7λ-1)\hat{j}+(-3λ+1)\hat{k}\\ \vec{r}=(2\hat{i}-\hat{j}+\hat{k})+λ(2\hat{i}+7\hat{j}-3\hat{k})

Question 9. The Cartesian equation of a line is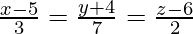\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2} . Write its vector form

Solution:

The Cartesian equation of the line is

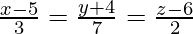\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2} ….(i)

The given line passes through the point (5, -4, 6). The position vector of this point is

\vec{a}=5\hat{i}-4\hat{j}+6\hat{k}

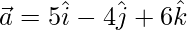
Also, the direction ratios of the given line are 3, 7 and 2.

This means that the line is in the direction of vector,

\vec{b}=3\hat{i}+7\hat{j}+2\hat{k}

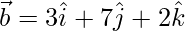
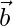It is known that the line through position vector\vec{a} and in the direction of the vector\vec{b} is given by the equation,

\vec{r}=\vec{a}+\lambda \vec{b}, \lambda ∈R\\ \vec{r}=(5\hat{i}-4\hat{j}+6\hat{k})+\lambda(3\hat{i}+7\hat{j}+2\hat{k})

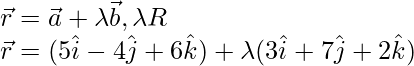
Question 10. Find the Cartesian equation of a line passing through (1, -1, 2) and parallel to the line whose equations are 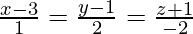\frac{x-3}{1}=\frac{y-1}{2}=\frac{z+1}{-2}. Also, reduce the equation obtained in vector form.

Solution:

We know that, equation of a line passing through a point (x1, y1, z1) and having direction ratios proportional to a, b, c is

\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\ \ \ \ \ ......(i)

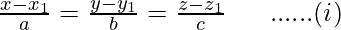
Here,

(x1, y1, z1) = (1, -1, 2) and

Given line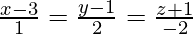\frac{x-3}{1}=\frac{y-1}{2}=\frac{z+1}{-2} is parallel to required line,

So,

a = μ, b = 2μ, c = -2μ

So, equation of required line using equation (i) is,

\frac{x-1}{μ }=\frac{y+1}{2μ }=\frac{z-2}{-2μ }\\ \frac{x-1}{1}=\frac{y+1}{2}=\frac{z-2}{-2}=\lambda

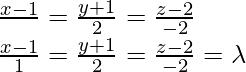
x = λ + 1, y = 2λ – 1, z = -2λ +2

So,

x\hat{i}+y\hat{j}+z\hat{k}=(λ+1)\hat{i}+(2λ+1)\hat{j}+(-2λ+ 2)\hat{k}\\ \vec{r}=(\hat{i}-\hat{j}+2\hat{k})+λ(\hat{i}+2\hat{j}-2\hat{k})


My Personal Notes arrow_drop_up
Like Article
Save Article
Related Articles
1. Class 12 RD Sharma Solutions - Chapter 28 The Straight Line in Space - Exercise 28.1 | Set 2
2. Class 12 RD Sharma Solutions - Chapter 28 The Straight Line in Space - Exercise 28.2 | Set 2
3. Class 12 RD Sharma Solutions - Chapter 28 The Straight Line in Space - Exercise 28.2 | Set 1
4. Class 12 RD Sharma Solutions- Chapter 28 The Straight Line in Space - Exercise 28.4
5. Class 12 RD Sharma Solutions - Chapter 28 The Straight Line in Space - Exercise 28.5
6. Class 12 RD Sharma Solutions - Chapter 28 The Straight Line in Space - Exercise 28.3
7. Class 11 RD Sharma Solutions - Chapter 23 The Straight Lines- Exercise 23.12 | Set 3
8. Class 11 RD Sharma Solutions - Chapter 23 The Straight Lines- Exercise 23.1 | Set 1
9. Class 11 RD Sharma Solutions - Chapter 23 The Straight Lines- Exercise 23.1 | Set 2
10. Class 11 RD Sharma solutions - Chapter 23 The Straight Lines- Exercise 23.6 | Set 1
Previous
Class 12 RD Sharma Solutions - Chapter 27 Direction Cosines and Direction Ratios - Exercise 27.1
Next
Class 12 RD Sharma Solutions - Chapter 28 The Straight Line in Space - Exercise 28.1 | Set 2
Article Contributed By :
https://media.geeksforgeeks.org/auth/avatar.png
yashchuahan
@yashchuahan
Vote for difficulty
Article Tags :
Report Issue
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox

Start Your Coding Journey Now!