Question 1. Find the angle between the given planes:
(i) 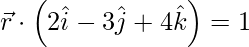 and
and 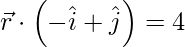
Solution:
Given
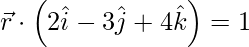 and
and 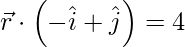
As we know that the angle between the planes 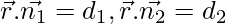 is given by,
is given by,
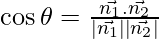
Here, 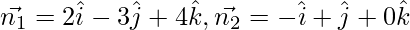
So, 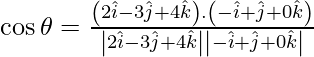
= 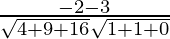
= 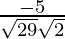
= 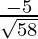
Therefore, 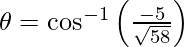 .
.
(ii) 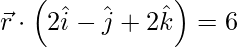 and
and 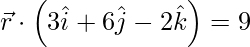
Solution:
Given
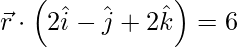 and
and 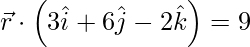
As we know that the angle between the planes 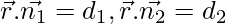 is given by,
is given by,
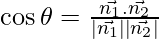
Here, 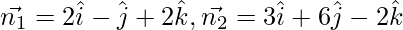
So, 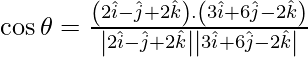
= 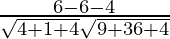
= 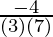
= -4/21
Therefore, θ = cos-1 (-4/21).
(iii) 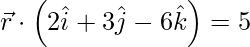 and
and 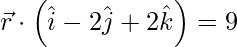
Solution:
Given
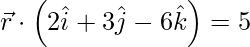 and
and 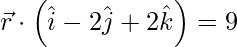
As we know that the angle between the planes, 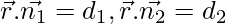 is given by,
is given by,
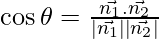
Here, 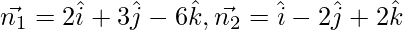
So, 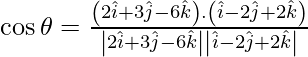
= 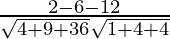
= 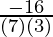
= -16/21
Therefore, θ = cos-1 (-16/21).
Question 2. Find the angle between the planes:
(i) 2x − y + z = 4 and x + y + 2z = 3
Solution:
Given, 2x − y + z = 4 and x + y + 2z = 3
As we know that the angle between the planes a1 x + b1 y + c1 z + d1 = 0 and a2 x + b2 y + c2 z + d2 = 0 is given by,
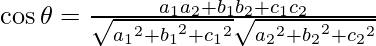
So, the angle between 2x – y + z = 4 and x + y + 2z = 3 is given by,
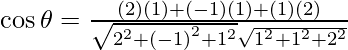
= 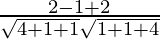
= 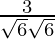
= 3/6
= 1/2
Therefore, θ = cos-1 (1/2) = π/3.
(ii) x + y − 2z = 3 and 2x − 2y + z = 5
Solution:
Given, x + y − 2z = 3 and 2x − 2y + z = 5
As we know that the angle between the planes a1 x + b1 y + c1 z + d1 = 0 and a2 x + b2 y + c2 z + d2 = 0 is given by,
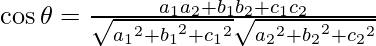
So, the angle between x + y – 2z = 3 and 2x – 2y + z = 5 is given by,
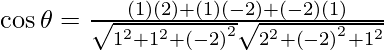
= 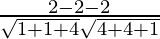
= 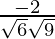
= -2/3√6
Therefore, θ = cos-1 (-2/3√6).
(iii) x − y + z = 5 and x + 2y + z = 9
Solution:
Given, x − y + z = 5 and x + 2y + z = 9
As we know that the angle between the planes a1 x + b1 y + c1 z + d1 = 0 and a2 x + b2 y + c2 z + d2 = 0 is given by,
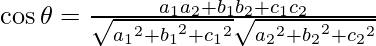
So, the angle between x – y + z = 5 and x + 2y + z = 9 is given by,
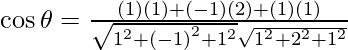
= 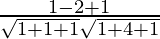
= 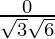
= 0
Therefore, θ = cos-1 (0) = π/2.
(iv) 2x − 3y + 4z = 1 and − x + y = 4
Solution:
Given, 2x − 3y + 4z = 1 and − x + y = 4
As we know that the angle between the planes a1 x + b1 y + c1 z + d1 = 0 and a2 x + b2 y + c2 z + d2 = 0 is given by,
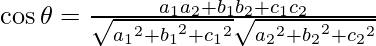
So, the angle between 2x – 3y + 4z = 1 and -x + y + 0z = 4 is given by,
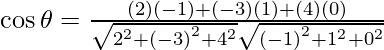
= 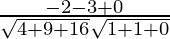
= 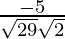
= 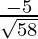
Therefore, 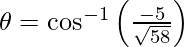 .
.
(v) 2x + y − 2z = 5 and 3x − 6y − 2z = 7
Solution:
Given, 2x + y − 2z = 5 and 3x − 6y − 2z = 7
As we know that the angle between the planes a1 x + b1 y + c1 z + d1 = 0 and a2 x + b2 y + c2 z + d2 = 0 is given by,
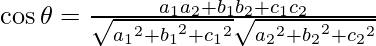
So, the angle between 2x + y – 2z = 5 and 3x – 6y – 2z = 7 is given by,
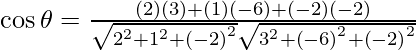
= 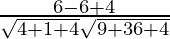
= 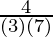
= 4/21
Therefore, θ = cos-1 (4/21).
Question 3. Show that the following planes are at right angles.
(i) 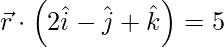 and
and 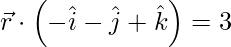
Solution:
Given, 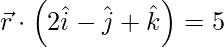 and
and 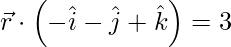
As we know that the planes 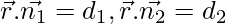 are perpendicular to each other only if
are perpendicular to each other only if 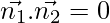 .
.
Here, 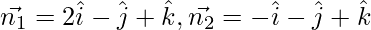
Now, we have
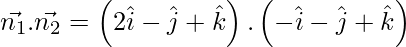
= -2 + 1 + 1
= 0
So, the given planes are perpendicular.
Hence proved.
(ii) x − 2y + 4z = 10 and 18x + 17y + 4z = 49
Solution:
Given, x − 2y + 4z = 10 and 18x + 17y + 4z = 49
As we know that the planes a1 x + b1 y + c1 z + d1 = 0 and a2 x + b2 y + c2 z + d2 = 0 are perpendicular to each other only if,
=> a1 a2 + b1 b2 + c1 c2 = 0
The given planes are x – 2y + 4z = 10 and 18x + 17y + 4z = 49.
Here, a1 = 1, b1 = – 2, c1 = 4, a2 = 18, b2 = 17 and c2 = 4
Now, we have
a1 a2 + b1 b2 + c1 c2 = (1) (18) + (- 2) (17) + (4) (4)
= 18 – 34 + 16
= 0
So, the given planes are perpendicular.
Hence proved.
Question 4. Determine the value of λ for which the following planes are perpendicular to each other.
(i) 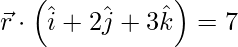 and
and 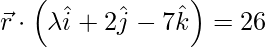
Solution:
Given, 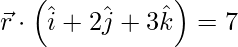 and
and 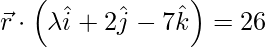
As we know that the planes, 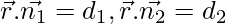 are perpendicular to each other only if,
are perpendicular to each other only if, 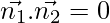 .
.
Here, 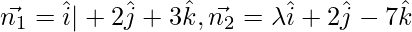
The given planes are perpendicular. So, we have
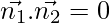
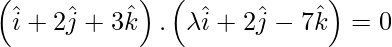
λ + 4 – 21 = 0
λ – 17 = 0
λ = 17
Therefore, the value of λ is 17.
(ii) 2x − 4y + 3z = 5 and x + 2y + λz = 5
Solution:
Given, 2x − 4y + 3z = 5 and x + 2y + λz = 5
As we know that the planes a1 x + b1 y + c1 z + d1 = 0 and a2 x + b2 y + c2 z + d2 = 0 are perpendicular to each other only if,
=> a1 a2 + b1 b2 + c1 c2 = 0
The given planes are 2x – 4y + 3z = 5 and x + 2y + λz = 5.
Here, a1 = 2, b1 = – 4, c1 = 3, a2 = 1, b2 = 2 and c2 = λ.
It is given that the given planes are perpendicular. So, we get
a1 a2 + b1 b2 + c1 c2 = 0
(2) (1) + (-4) (2) + (3) (λ) = 0
2 – 8 + 3λ = 0
3λ = 6
λ = 2
Therefore, the value of λ is 2.
(iii) 3x − 6y − 2z = 7 and 2x + y − λz = 5
Solution:
Given, 3x − 6y − 2z = 7 and 2x + y − λz = 5
As we know that the planes a1 x + b1 y + c1 z + d1 = 0 and a2 x + b2 y + c2 z + d2 = 0 are perpendicular to each other only if,
=> a1 a2 + b1 b2 + c1 c2 = 0
The given planes are 3x – 6y – 2z = 7 and 2x + y – λz = 5.
Here, a1 = 3, b1 = – 6, c1 = – 2, a2 = 2, b2 = 1 and c2 = -λ
Here, the given planes are perpendicular.
a1 a2 + b1 b2 + c1 c2 = 0
(3) (2) + (-6) (1) + (-2) (λ) = 0
6 – 6 + 2λ = 0
2λ = 0
λ = 0
Question 5. Find the equation of a plane passing through the point (−1, −1, 2) and perpendicular to the planes 3x + 2y − 3z = 1 and 5x − 4y + z = 5.
Solution:
The equation of any plane passing through (-1, -1, 2) is,
a (x + 1) + b (y + 1) + c (z – 2) = 0 . . . . (1)
It is given that the above equation is perpendicular to each of the planes 3x + 2y – 3z = 1 and 5x – 4y + z = 5.
3a + 2b – 3c = 0 . . . . (2)
5a – 4b + c = 0 . . . . (3)
On solving eq (1), (2) and (3), we get,
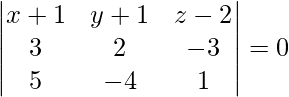
-10 (x + 1) – 18 (y + 1) – 22 (z – 2) = 0
-5 (x + 1) – 9 (y + 1) – 11 (z – 2) = 0
5x + 5 + 9y + 9 + 11z – 22 = 0
5x + 9y + 11z – 8 = 0
Hence, the equation of the plane is 5x + 9y + 11z – 8 = 0
Question 6. Obtain the equation of the plane passing through the point (1, −3, −2) and perpendicular to the planes x + 2y + 2z = 5 and 3x + 3y + 2z = 8.
Solution:
The equation of any plane passing through (1, -3, -2) is,
a (x – 1) + b (y + 3) + c (z + 2) = 0 . . . . (1)
It is given that above equation is perpendicular to the planes x + 2y + 2z = 5 and 3x + 3y + 2z = 8.
a + 2b + 2c = 0 . . . . (2)
3a + 3b + 2c = 0 . . . . (3)
On solving eq (1), (2) and (3), we get,
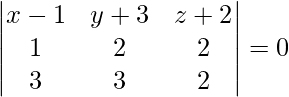
-2 (x – 1) + 4 (y + 3) – 3 (z + 2) = 0
-2x + 2 + 4y + 12 – 3z – 6 = 0
2x – 4y + 3z – 8 = 0
Hence, the equation of the plane is 2x – 4y + 3z – 8 = 0
Question 7. Find the equation of the plane passing through the origin and perpendicular to each of the planes x + 2y − z = 1 and 3x − 4y + z = 5.
Solution:
The equation of any plane passing through the origin (0, 0, 0) is,
a (x – 0) + b (y – 0) + c (z – 0) = 0 . . . . (1)
ax + by + cz = 0
It is given that above equation is perpendicular to the planes x + 2y – z = 1 and 3x – 4y + z = 5 .
a + 2b – c = 0 . . . . (2)
3a – 4b + c = 0 . . . . (3)
On solving eq(1), (2) and (3), we get,
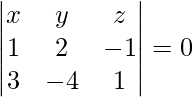
– 2x – 4y – 10z = 0
x + 2y + 5z = 0
Hence, the equation of the plane is x + 2y + 5z = 0
Question 8. Find the equation of the plane passing through the points (1, −1, 2) and (2, −2, 2) and which is perpendicular to the plane 6x − 2y + 2z = 9.
Solution:
The equation of any plane passing through (1, -1, 2) is,
a (x – 1) + b (y + 1) + c (z – 2) = 0 . . . . (1)
It is given that above equation is passing through (2, -2, 2). So,
a (2 – 1) + b (-2 + 1) + c (2 – 2) = 0
a – b = 0 . . . . (2)
It is given that above equation is perpendicular to the plane 6x – 2y + 2z = 9. So,
6a – 2b + 2c = 0
3a – b + c = 0 . . . . (3)
On solving eq(1), (2) and (3), we get,
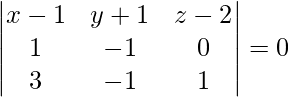
-1 (x – 1) – 1 (y + 1) + 2 (z – 2) = 0
– x + 1 – y – 1 + 2z – 4 = 0
x + y – 2z + 4 = 0
Hence, the equation of the plane is x + y – 2z + 4 = 0
Question 9. Find the equation of the plane passing through the points (2, 2, 1) and (9, 3, 6) and perpendicular to the plane 2x + 6y + 6z = 1.
Solution:
The equation of any plane passing through (2, 2, 1) is,
a (x – 2) + b (y – 2) + c (z – 1) = 0 . . . . (1)
It is given that the above equation is passing through (9, 3, 6). So,
a (9 – 2) + b (3 – 2) + c (6 – 1) = 0
7a + b + 5c = 0 . . . . (2)
It is given that the above equation is perpendicular to the plane 2x + 6y + 6z = 1. So,
2a + 6b + 6c = 0
a + 3b + 3c = 0 . . . . (3)
On solving eq(1), (2) and (3), we get
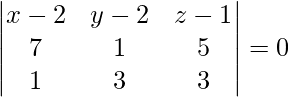
-12 (x – 2) – 16 (y – 2) + 20 (z – 1) = 0
3 (x – 2) + 4 (y – 2) – 5 (z – 1) = 0
3x + 4y – 5z = 9
Hence, the equation of the plane is 3x + 4y – 5z = 9
Question 10. Find the equation of the plane passing through the points whose coordinates are (−1, 1, 1) and (1, −1, 1) and perpendicular to the plane x + 2y + 2z = 5.
Solution:
The equation of any plane passing through (-1, 1, 1) is,
a (x + 1) + b (y – 1) + c (z – 1) = 0 . . . . (1)
It is given that the above equation passed through (1, -1, 1). So,
a (1 + 1) + b (-1 – 1) + c (1 – 1) = 0
2a – 2b = 0 . . . . (2)
It is given that the above equation is perpendicular to the plane x + 2y + 2z = 5. So,
a + 2b + 2c = 0 . . . . (3)
On solving eq(1), (2) and (3), we get
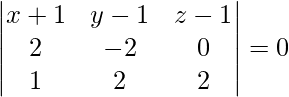
-4 (x + 1) – 4 (y – 1) + 6 (z – 1) = 0
2 (x + 1) + 2 (y – 1) – 3 (z – 1) = 0
2x + 2y – 3z + 3 = 0
Hence, the equation of the plane is 2x + 2y – 3z + 3 = 0
Question 11. Find the equation of the plane with intercept 3 on the y-axis and parallel to the ZOX plane.
Solution:
The equation of the plane parallel to the plane ZOX is,
y = b . . . . (1)
According to the question, it is given that this plane passes through (0, 3, 0). So,
=> b = 3
On substituting this value in eq(1), we get
y = 3,
Hence, the equation of the plane is
y = 3
Question 12. Find the equation of the plane that contains the point (1, −1, 2) and is perpendicular to each of the planes 2x + 3y − 2z = 5 and x + 2y − 3z = 8.
Solution:
The equation of any plane passing through (1, -1, 2) is,
a (x – 1) + b (y + 1) + c (z – 2) = 0 . . . . (1)
It is given that the above equation is perpendicular to the plane 2x + 3y – 2z = 5. So,
2a + 3b – 2c = 0 . . . . (2)
It is given that the above equation is perpendicular to the plane x + 2y – 3z = 8. So,
a + 2b – 3c = 0 . . . . (3)
So, on solving eq (1), (2) and (3), we get
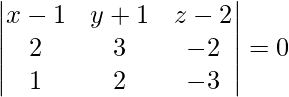
-5 (x – 1) + 4 (y + 1) + 1 (z – 2) = 0
5x – 4y – z = 7
Hence, the equation of the plane is 5x – 4y – z = 7
Question 13. Find the equation of the plane passing through (a, b, c) and parallel to the plane 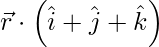 = 2.
= 2.
Solution:
Given equation of the plane is \vec{r} \cdot \left( \hat{i} + \hat{j} + \hat{k} \right) = 2
So, on substituting 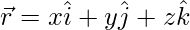 in the given equation of the plane, we get
in the given equation of the plane, we get
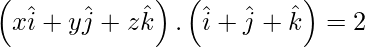
=> x + y + z – 2 = 0 . . . . (1)
The equation of a plane which is parallel to plane (eq 1) is of the form,
x + y + z = k . . . . (2)
It is given that above equation of plane is passing through the point (a, b, c). So,
a + b + c = k
On substituting this value of k in eq(2), we get
x + y + z = a + b + c
Hence, the equation of the plane is
x + y + z = a + b + c
Question 14. Find the equation of the plane passing through the point (−1, 3, 2) and perpendicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.
Solution:
The equation of any plane passing through point (-1, 3, 2) is,
a (x + 1) + b (y – 3) + c (z – 2) = 0 . . . . (1)
It is given that the above equation is perpendicular to the plane x + 2y + 3z = 5. So,
a + 2b + 3c = 0 . . . . (2)
It is given that the above equation is perpendicular to the plane 3x + 3y + z = 0. So,
3a + 3b + c = 0 . . . . (3)
On solving eq (1), (2) and (3), we get
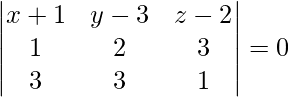
-7 (x + 1) + 8 (y – 3) – 3 (z – 2) = 0
7x – 8y + 3z + 25 = 0
Hence, the equation of the plane is
7x – 8y + 3z + 25 = 0
Question 15. Find the vector equation of the plane through the points (2, 1, −1) and (−1, 3, 4) and perpendicular to the plane x − 2y + 4z = 10.
Solution:
The equation of any plane passing through (2, 1, -1) is,
a (x – 2) + b (y – 1) + c (z + 1) = 0 . . . . (1)
It is given that the above equation passes through (-1, 3, 4). So,
a (-1 – 2) + b (3 – 1) + c (4 + 1) = 0
-3a + 2b + 5c . . . . (2)
It is given that the above equation is perpendicular to the plane x – 2y + 4z = 10. So,
a – 2b + 4c = 0 . . . . (3)
On solving eq (1), (2) and (3), we get
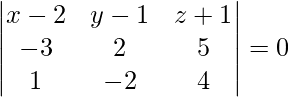
18 (x – 2) + 17 (y – 1) + 4 (z + 1) = 0
18x + 17y + 4z – 49 = 0
Hence, the equation of the plane is
18x + 17y + 4z – 49 = 0
Share your thoughts in the comments
Please Login to comment...