Question 1. Find the points of local maxima or local minima and corresponding local maximum and local minimum values of the following function. Also, find the points of inflection, if any:
(i) f(x) = x4 – 62x2 + 120x + 9
Solution:
Given function: f(x) = x4 – 62x2 + 120x + 9
Differentiating with respect to x
f'(x) = 4x3 – 124x + 120 = 4(x3 – 31x + 30)
Again differentiating with respect to x
f”(x) = 12x2 – 124 = 4(3x2 – 31)
Now, for maxima and minima
Put f'(x) = 0
⇒ 4(x3 – 31x + 30) = 0
⇒ x3 – 31x + 30 = 0
⇒ x = 5, 1, -6
Now,
f”(5) = 176 > 0
⇒ x = 5 is point of local minima
f”(1) = -112 < 0
⇒ x = 1 is point of local maxima
f”(-6) = 308 > 0
⇒ x = -6 is point of local minima
Now, we find the local maximum value = f(1) = 68
and local minimum value = f(5) = -316
and = f(-6) = -1647
(ii) f(x) = x3 – 6x2 + 9x + 15
Solution:
Given function: f(x) = x3 – 6x2 + 9x +15
Differentiating with respect to x
f'(x) = 3x2 -12x + 9 = 3(x2 – 4x + 3)
Again differentiating with respect to x
f”(x) = 6x – 12
Now, for maxima and minima
Put f'(x) = 0
⇒ 3(x2 – 4x + 3) = 0
⇒ x2 – 4x + 3 = 0
⇒ (x – 3)(x – 1) = 0
⇒ x = 3, 1
Now,
f”(3) = 6 > 0
⇒ x = 3 is point of local minima
f”(1) = -6 < 0
⇒ x = 1 is point of local maxima
⇒ x = -6 is point of local minima
Now we find the local maximum value = f(1) =19
and local minimum value = f(3) = 15
(iii) f(x) = (x – 1)(x + 2)2
Solution:
Given function: f(x) = (x – 1)(x + 2)2
Differentiating with respect to x
f ‘(x) = (x + 2)2 + 2(x – 1)(x + 2)
= (x + 2)(x + 2 + 2x – 2)
= (x + 2)(3x)
Again differentiating with respect to x
f ”(x) = 3(x + 2) + 3x
= 6x + 6
For maxima and minima
Put f'(x) = 0
⇒ 3x(x + 2) = 0
⇒ x = 0, -2
Now,
f”(0) = 6 > 0
⇒ x = 0 is point of local minima
f”(-2) = -6 < 0
⇒ x = -2 is point of local maxima
Now we find the local maximum value = f(-2) =0
Local minimum value = f(0) = -4
(iv) f(x) = 2/x – 2/x2, x > 0
Solution:
Given function: f(x) = 2/x – 2/x2, x > 0
Differentiating with respect to x
f'(x) = -2/x2 + 4/x3
Again differentiating with respect to x
f”(x) = -4/x3 – 12/ x4
For maxima and minima
Put f'(x) = 0
⇒ -2/x2 + 4/x3 = 0
⇒ -2(x – 2)/x3 = 0
⇒ x = 2
Now,
f”(2) = 4/8 – 12/6 = 1/2 – 3/4 = -1/4 < 0
⇒ x = 2 is point of local maxima
Now, local maximum value = f(2) = 1/2
(v) f(x) = xex
Solution:
Given function: f(x) = xex
Differentiating with respect to x
f'(x) = ex + xex = ex(x + 1)
Again differentiating with respect to x
f”(x) = ex(x + 1) + ex = ex(x + 2)
For maxima and minima
Put f'(x) = 0
⇒ ex(x + 1) = 0
⇒ x = -1
Now,
f”(-1) = e-1 = 1/e > 0
⇒ x = -1 is point of local minima
Now, local minimum value = f(-1) = -1/e
(vi) f(x) = x/2 + 2/x, x > 0
Solution:
Given function: f(x) = x/2 + 2/x, x > 0
Differentiating with respect to x
f'(x) = 1/2 – 2/x2
Again differentiating with respect to x
f”(x) = 4/x3
For maxima and minima
Put f'(x) = 0
⇒ 1/2 – 2/x2 = 0
⇒ (x2 – 4)/2x2 = 0
⇒ x = -2, +2
Now,
f”(2) = 4/8 = 1/2 > 0
Thus, x = 2
x=-2 not taken because x > 0 is given.
Now, local minimum value = f (2) = 2
(vii) f(x) = (x + 1)(x + 2)1/3, x ≥ -2
Solution:
Given function: f(x) = (x + 1)(x + 2)1/3, x ≥ -2
Differentiating with respect to x
f ‘(x) = (x + 2)1/3 + 1/3(x + 1)(x + 2)-2/3
= (x + 2)-2/3(x + 2 + 1/3(x + 1))
= 1/3(x + 2)-2/3(4x + 7)
Again differentiating with respect to x
f”(x) = -2/9(x + 2)-5/3(4x + 7) + 1/3(x + 2)-2/3 × 4
For maxima and minima
Put f'(x) = 0
⇒ 1/3(x + 2)-2/3(4x + 7) = 0
⇒ (4x + 7) = 0
⇒ x = -7/4
Now,
f “(-7/4) = 4/3(-7/4 + 2)-2/3
Thus, x = -7/4 is point of local minima
Now, local minimum value = f(-7/4) = 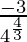
(viii) f(x) = x , -5 ≤ x ≤ 5
, -5 ≤ x ≤ 5
Solution:
Given function: f(x)=x , -5 ≤ x ≤ 5
, -5 ≤ x ≤ 5
Differentiating with respect to x
f'(x) = 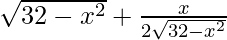 × (-2x)
× (-2x)
= 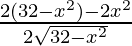
= 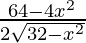
Again differentiating with respect to x
f”(x) = 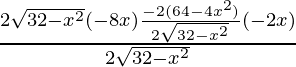
= 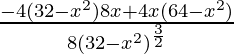
For maxima and minima
Put f'(x) = 0
⇒ 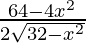 = 0
= 0
⇒ 64 – 4x2 = 0
⇒ x = ±4
Now,
f”(4) = 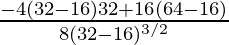 <0
<0
Thus, x = 4 is point of maxima
Now, local maximum value = f(4) = 16
x = -4 is point of minima
Now, local minimum value = f(-4) = -16
(ix) f(x) = x3 – 2ax2 + a2x, a > 0, x ∈ R
Solution:
Given function: f(x) = x3 – 2ax2 + a2x
Differentiating with respect to x
f ‘(x) = 3x2 – 4ax + a2
Again differentiating with respect to x
f”(x) = 6x – 4a
For maxima and minima
Put f'(x) = 0
⇒ 3x2 – 4ax + a2 = 0
⇒ x = 
= (4a ± 2a)/6 = a, a/3
Now,
f”(a) = 2a > 0 as a > 0
x = a is point of local minima
f”(a/3) = -2a < 0 as a < 0
x = a/3 is point of local maxima
Hence,
The local maximum value = f(a/3) = 4a3/27
and local minimum value = f(a) = 0
(x) f(x) = x + a2/x, a > 0, x ≠ 0
Solution:
Given function: f(x) = x + a2/x
Differentiating with respect to x
f’ (x) = 1 – a2/x2
Again differentiating with respect to x
f”(x) = 2a2/x3
For maxima and minima
Put f'(x) = 0
⇒ 1 – a2/x2 = 0
⇒ x2 – a2 = 0
x = ± a
Now,
f”(a) = 2/a > 0 as a > 0
x = a is point of minima
f”(-a) = -2/a < 0 as a > 0
x = -a is point of maxima
Hence, the local maximum value = f(-a) = -2a
and local minimum value = f(a) = 2a
(xi) f(x) = 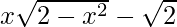 , −√2 ≤ x ≤ √2
, −√2 ≤ x ≤ √2
Solution:
Given function: f(x) = 
Differentiating with respect to x
f'(x) = 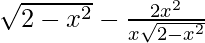
= 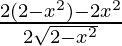
= 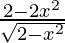
Again differentiating with respect to x
f”(x) = 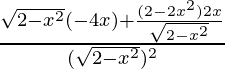
= 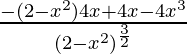
For maxima and minima
Put f'(x) = 0
⇒ 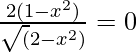
⇒x = ±1
Now,
f”(1) < 0
⇒ x = 1 is point of local maxima
f”(-1) > 0
⇒ x = -1 is point of local maxima
Hence, the local maximum value = f (1) = 1
and local minimum value = f (-1) = -1
(xii) 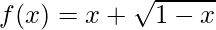 , x ≤ 1
, x ≤ 1
Solution:
Given function: f(x) = x + 
Differentiating with respect to x
f'(x) = 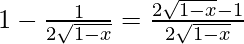
f'(x) = 
For maxima and minima
Put f'(x) = 0
⇒ 
⇒ 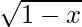 =1/2
=1/2
⇒ x= 1 – 1/4 = 3/4
Now,
f”(3/4) < 0
⇒ x = 3/4 is point of local maxima
Hence, the local maximum value = f (3/4) = 5/4
Question 2. Find the local extremum values of the following functions:
(i) f (x) = (x – 1)(x – 2)2
Solution:
Given function: f(x) = (x – 1)(x – 2)2
Differentiating with respect to x
f'(x) = (x – 2)2 + 2(x – 1)(x – 2)
= (x – 2)(x – 2 + 2x – 2)
= (x – 2)(3x – 4)
Again differentiating with respect to x
f”(x) =(3x – 4) + 3(x – 2)
For maxima and minima
Put f'(x) = 0
⇒ (x – 2)(3x – 4) = 0
⇒ x = 2, 4/3
Now,
f”(2) > 0
x = 2 is local minima
f “(4/3) = -2 < 0
x = 4/3 is point of local maxima
Hence, the local maximum value = f(4/3) = 4/27
and the local minimum value = f(2) =0
(ii) f (x) = x , x ≤ 1
, x ≤ 1
Solution:
Given function: f (x) = x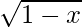
Differentiating with respect to x
f ‘(x) = 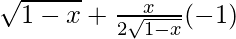
= 
= (2 – 3x)/2
Again differentiating with respect to x
f”(x) = 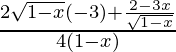
For maxima and minima
Put f'(x) = 0
⇒ (2 – 3x)/2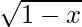 =0
=0
⇒ x = 2/3
Now,
f “(2/3) < 0
x = 2/3 is point of maxima
Hence, the local maximum value = f (2/3) = 2/3√3
(iii) f(x) = -(x – 1)3(x + 1)2
Solution:
Given function: f(x) = -(x – 1)3(x + 1)2
Differentiating with respect to x
f ‘(x) = -3(x – 1)2 (x + 1)2 – 2(x – 1)3 (x + 1)
= -(x – 1)2 (x + 1) (3x + 3 + 2x – 2)
= -(x – 1)2(x + 1) (5x + 1)
Again differentiating with respect to x
f”(x) = -2(x – 1) (x + 1) (5x + 1) – (x – 1)2 (5x + 1) – 5 (x – 1)2 (x + 1)
For maxima and minima
Put f'(x) = 0
⇒ -(x – 1)2 (x + 1) (5x + 1) = 0
⇒ x = 1, -1, -1/5
Now,
f”(1) = 0
x = 1 is inflection point
f “(-1) = -4 × -4 = 16 > 0
x = -1 is point of minima
f”(-1/5) = -5(36/25) × (4/5) = -144/25 < 0
x = -1/5 is point of maxima
Hence, the local maximum value = f (-1/5) = 3456/3125
and the local minimum value = f (-1) = 0
Question 3. The function y = a log x + bx2 + x has extreme values at x = 1 and x = 2. Find a and b.
Solution:
We have,
y = alogx + bx2 + x
Differentiating with respect to x
dy/dx = a/x + 2bx + 1
Again differentiating with respect to x
d2y/dx2 = -a/x2 +2b
For maxima and minima
Put dy/dx = 0
⇒ a/x + 2bx +1 = 0
Given that extreme value exist at x = 1, 2
⇒ a + 2b = -1 …..(i)
a/2 + 4b = -1
⇒ a + 8b = -2 …..(ii)
On solving eq(i) and (ii), we get
a = -2/3, b = -1/6
Question 4. Show that (log x / x) has a maximum value at x = e.
Solution:
Given function: f(x) = logx / x
Differentiating with respect to x
f'(x)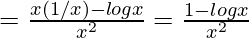
Now, f'(x) = 0
⇒ 1 – logx = 0
⇒ logx = 1
⇒ logx = loge
⇒ x = e
Again differentiating with respect to x
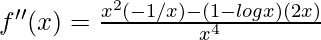
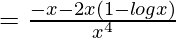
= 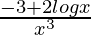
Now, f ”(e) = 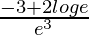
=(-3 + 2)/e3 = -1/e3 < 0
Therefore, by second derivative test, f is the maximum at x = e.
Question 5. Find the maximum and minimum values of the function f (x) = 4/(x + 2) + x.
Solution:
Given function: f(x) = 4/(x + 2) + x
Differentiating with respect to x
f'(x) = -4/(x + 2)2 + 1
Again differentiating with respect to x
f”(x) = 8/(x + 2)3
For maxima and minima
Put f'(x) = 0
⇒ -4/(x + 2)2 + 1 = 0
⇒ (x + 2)2 = 4
⇒ x2 + 4x = 0
⇒ x (x + 4) = 0
x = 0, -4
Now,
f ”(0) = 1 > 0
x = 0 is point of minima
f ”(-4) = -1 < 0
x = -4 is point of maxima
Hence, the local maximum value = f (-4) = -6
and the local minimum value = f (0) = 2
Question 6. Find the maximum and minimum values of f (x) = tan x – 2x.
Solution:
Given function: f(x) = tanx – 2x
Differentiating with respect to x
f'(x) = sec2x – 2
Again differentiating with respect to x
f”(x) = 2sec2x tanx
For maxima and minima
Put f'(x) = 0
⇒ sex2x = 2
⇒ secx = ±√2
⇒ x = π/4, 3π/4
f”(π/4) = 4 > 0
x = π/4 is point of minima
f”(3π/4) = -4 < 0
x = (3π/4) is point of maxima
Hence, the maximum value = f (3π/4) = -1 – 3π/2
and the minimum value = f (π/4) = 1 – π/2
Question 7. If f(x) = x3 + ax2 + b x + c has a maximum at x = -1 and minimum at x = 3. Determine a, b and c.
Solution:
Given function: f(x) = x3 + ax2 + b x + c
Differentiating with respect to x
f ‘(x) = 3x2 + 2ax + b
It is given that f (x) is maximum at x = -1
f ‘(-1) = 3(-1)2 + 2a(-1) + b = 0
f ‘(-1) = 3 – 2a + b = 0 …….(i)
At x = 3, f(x) is minimum
f ‘(3) = 3(3)2 + 2a(3) + b = 0
⇒ f ‘(3) = 27 + 6a +b = 0 …..(ii)
On solving eq(i) and (ii), we get
a = -3 and b = -9
Since f ‘(x) is independent of constant c, so, it can be any real number.
Share your thoughts in the comments
Please Login to comment...