Class 12 RD Sharma Solutions – Chapter 10 Differentiability – Exercise 10.2
Last Updated :
16 May, 2021
Question 1. If f is defined by f(x) = x2, find f'(2).
Solution:
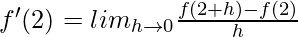
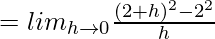
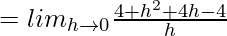
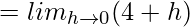
Hence, f'(2) = 4.
Question 2. If f is defined by f(x) = x2 – 4x + 7, show that f'(5) = 2f'(7/2).
Solution:
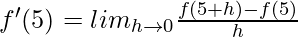
= 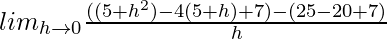
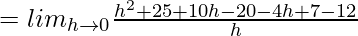
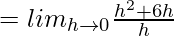
f'(5) = 6 …….(1)
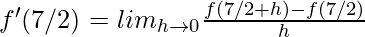
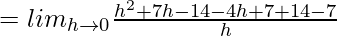
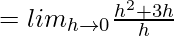
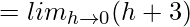
f'(7/2) = 3
⇒ 2f'(7/2) = 6 ……(2)
From (1) and (2)
f'(5) = 2f'(7/2).
Question 3. Show that the derivative of the function f given by f(x) = 2x3 – 9x2 +12x + 9 at x = 1 and x = 2 are equal.
Solution:
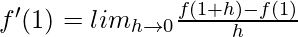
![Rendered by QuickLaTeX.com = lim_{h\to0}\frac{[2(1+h)^2-9(1+h)^2+12(1+h)+9]-[2-9+12-9]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1b5140e22ff0127dcae50241df50dcc2_l3.png)
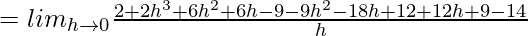
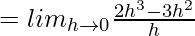
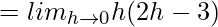
⇒ f'(1) = 0
Now, 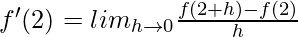
![Rendered by QuickLaTeX.com = lim_{h\to0}\frac{[2(2+h)^3-9(2+h)^2+12(2+h)+9]-[16-36+24+9]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c6d41f85dd2b00d75d73819e3bb48a9d_l3.png)
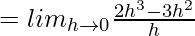
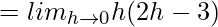
⇒ f'(2) = 0
Hence f'(1) = f'(2) = 0.
Question 4. If for the function f(x) = ax2 + 7x – 4, f'(5) = 97, find a.
Solution:
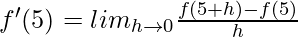
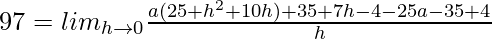
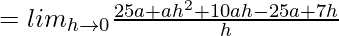
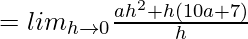
⇒ 97 = 10a +7
⇒ 10a = 90
⇒ a = 9
Question 5. If f(x) = x3 + 7x2 + 8x – 9, find f'(4).
Solution:
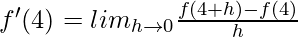
![Rendered by QuickLaTeX.com = lim_{h\to0}\frac{[(4+h)^3+7(4+h)^2+8(4+h)-9]-[64+112+32-9]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dd486210fac4a345eb333c52cb3baccc_l3.png)
![Rendered by QuickLaTeX.com = lim_{h\to0}\frac{64+h^3+48h+12h^2+112+7h^2+56h+32+8h-9]-[210-9]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9c5c55cae69f0dbf174527377b3053ba_l3.png)
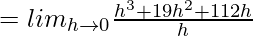
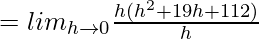
⇒ f'(4) = 112
Question 6. Find the derivative of f(x) = mx + c at x = 0.
Solution:
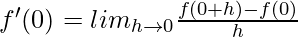
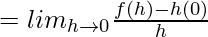
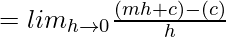
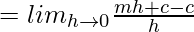
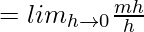
⇒ f'(0) = m.
Question 7. Examine the differentiability of 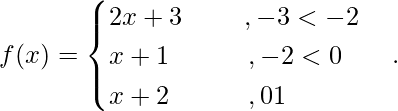
Solution:
Since f(x) is a polynomial function, it is continuous and differentiable everywhere.
Differentiability at x = –2
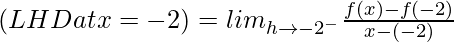
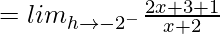
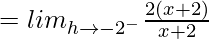
= 2
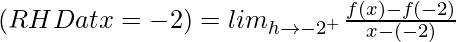
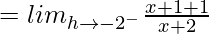
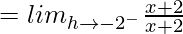
= 1
Since, LHD at x = –2 ≠ RHD at x = –2
Hence f(x) is not differentiable at x = –2.
Now, Differentiability at x = 0
(LHD at x = 0) 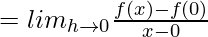
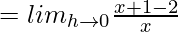
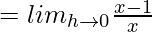
= ∞
(RHD at x = 0) 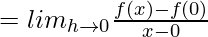
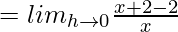
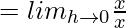
= 1
Since, LHD at x = –2 ≠ RHD at x = 0
Hence f(x) is not differentiable at x = 0.
Question 8. Write an example of a function which is everywhere continuous but fails to be differentiable at exactly five points.
Solution:
We know the modulus function f(x) = |x| is continuous but not differentiable at x = 0.
Hence, f(x) = |x| + |x – 1| + |x – 2| + |x – 3| + |x – 4| is continuous but not fails to be differentiable at x = 0,1,2,3,4.
Question 9. Discuss the continuity and differentiability of f(x) = |log|x||.
Solution:
Graph of f(x) = |log|x||:

From the graph above, it is clear that f(x) is continuous everywhere, but not differentiable at 1 and -1.
Question 10. Discuss the continuity and differentiability of f(x) = e|x|.
Solution:
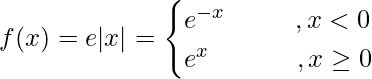
For continuity:
(LHL at x = 0) 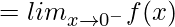
= 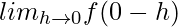
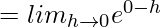
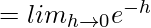
= e0
= 1
(RHL at x = 0) 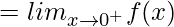
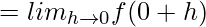
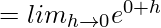
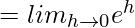
= e0
= 1
Hence f(x) is continuous at x = 0.
For Differentiability:
(LHD at x = 0) = 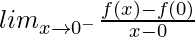
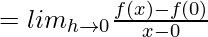
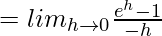
= –1
(RHD at x = 0) 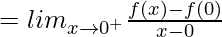
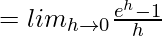
= 1
Thus, f(x) is not differentiable at x = 0.
Question 11. Discuss the differentiability of 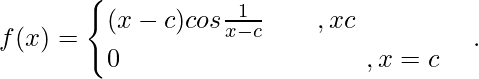
Solution:
(LHD at x = c) 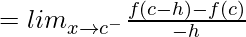
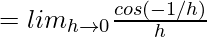
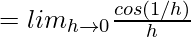
= k
(RHD at x = c) = 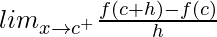
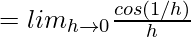
= k
Clearly (LHD at x = c) = (RHD at x = c)
f(x) is differentiable at x = c.
Question 12. Is |sinx| differentiable? What about cos|x|?
Solution:
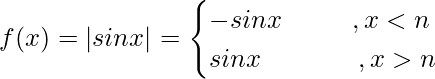
(LHD at x = nπ) 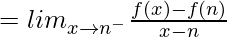
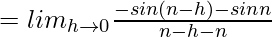
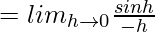
= –1
(RHD at x = nπ) 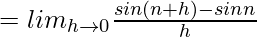
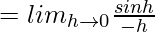
= 1
Since, LHD at x = nπ ≠ RHD at x = nπ
Hence f(x) = |sinx| is not differentiable at x = nπ.
Now, f(x) = cos|x|
Since, cos(–x) = cosx
Thus, f(x) = cos x
Hence f(x) = cos|x| is differentiable everywhere.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...