Class 12 RD Sharma Solutions – Chapter 29 The Plane – Exercise 29.4
Last Updated :
16 May, 2021
Question 1. Find the vector equation of a plane which is at a distance of 3 units from the origin and has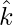 as the unit vector normal to it.
as the unit vector normal to it.
Solution:
We know, the vector equation of a plane normal to unit vector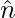 and at a distance of d from origin is given as
and at a distance of d from origin is given as

Here, d = 3 units ,we get
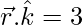
Question 2. Find the vector equation of a plane which is at a distance of 5 units from the origin and which is normal to the vector
Solution:
We know, the vector equation of a plane normal to unit vector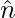 and at a distance of d from origin is given as
and at a distance of d from origin is given as

Here, d = 5 units
and
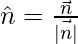
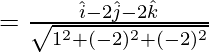
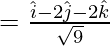
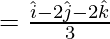
Hence the required equation is,
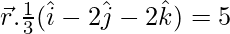
Question 3. Reduce the equation 2x – 3y – 6z = 14 to the normal form and hence find the length of perpendicular from the origin to the plane. Also, find the direction of cosines of normal to the plane.
Solution:
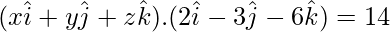
Dividing the equation by

![Rendered by QuickLaTeX.com ⇒ \vec{r}.[\frac{2}{7}\hat{i} - \frac{3}{7}\hat{j} - \frac{6}{7}\hat{k}] = 2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1559b74f3fffec54dde922abadd9c397_l3.png) ……(1)
……(1)
Since Vector equation of a plane with distance d and normal to the unit vector n is given by
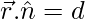 ……(2)
……(2)
Comparing (1) and (2), we get
Distance from origin = 2 units
Direction cosine of normal to plane =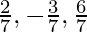
Question 4. Reduce the equation to the normal form and hence find the length of perpendicular from origin to the plane.
to the normal form and hence find the length of perpendicular from origin to the plane.
Solution:

Multiplying both sides by –1, we get
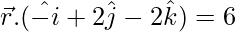
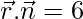 …..(1)
…..(1)
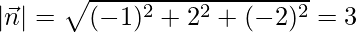
Dividing (1) by 3 on both sides,
![Rendered by QuickLaTeX.com \vec{r}.[-\frac{\hat{i}}{3} + \frac{2}{3}\hat{j} - \frac{2}{3}\hat{k}] = 2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e944b7d6c41839e0781fac1d286ff61a_l3.png)
Since vector equation of a plane with distance d and normal to the unit vector n is given by
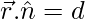 ……(2)
……(2)
Comparing (1) and (2), we get
d = 2
![Rendered by QuickLaTeX.com \hat{n} = [-\frac{\hat{i}}{3} + \frac{2}{3}\hat{j} - \frac{2}{3}\hat{k}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a4b43c101143545878a0498dd620dfbd_l3.png)
Length of normal = 2 units.
Question 5. Write the normal form of the equation 2x – 3y + 6z + 14 = 0.
Solution:
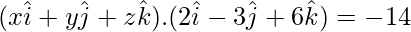
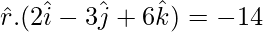
Multiplying both sides by –1, we get
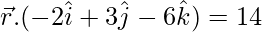
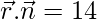 …..(1)
…..(1)
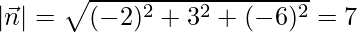
Dividing (1) by 7 on both sides,
![Rendered by QuickLaTeX.com \vec{r}.[-\frac{2}{3}\hat{i} + \frac{3}{7}\hat{j} - \frac{6}{7}\hat{k}] = 2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-13006bb56d074cbca3f043e753956127_l3.png)
Hence normal form of the equation is
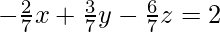
Question 6. The direction ratios of the perpendicular from the origin to a plane are 12, –3, 4 and the length of the perpendicular is 5. Find the equation of the plane.
Solution:
Normal vector =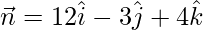
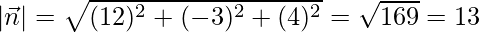
So, Normal unit vector
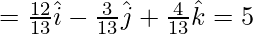
Since vector equation of a plane with distance d and normal to the unit vector n is given by

![Rendered by QuickLaTeX.com ⇒ \vec{r}.[\frac{12}{13}\hat{i} - \frac{3}{13}\hat{j} + \frac{4}{13}\hat{k}] = 5](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-658329ae65d0903c2527464ee09a0f64_l3.png)
or,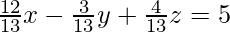
Question 7. Find the unit normal vector to the plane x + 2y + 3z – 6 = 0.
Solution:
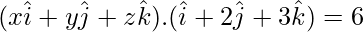
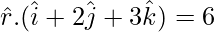
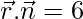 …….(1)
…….(1)
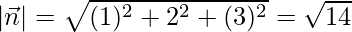
Dividing (1) by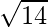 , we get
, we get
![Rendered by QuickLaTeX.com \vec{r}.[\frac{1}{\sqrt14}\hat{i} + \frac{2}{\sqrt14}\hat{j} + \frac{3}{\sqrt14}\hat{k}] = \frac{6}{\sqrt14}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d06b436878c6dfbb4ef74f1c94a64257_l3.png)
Since vector equation of a plane with distance d and normal to the unit vector n is given by
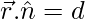 …..(2)
…..(2)
Thus, normal unit vector =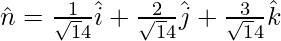
Question 8. Find the equation of a plane which is at a distance of 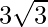 units from the origin and the normal to which is equally inclined with the coordinate axes.
units from the origin and the normal to which is equally inclined with the coordinate axes.
Solution:
Since vector equation of a plane with distance d and normal to the unit vector n is given by

d =
Let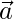 be a normal vector,
be a normal vector,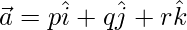
Since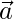 is equally inclined to the coordinate axes, let l, m, n be the cosines of
is equally inclined to the coordinate axes, let l, m, n be the cosines of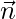 . Also l = m = n.
. Also l = m = n.
We know, l2 + m2 + n2 = 1
or,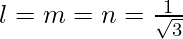
Now,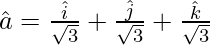
Vector equation of the required plane is
![Rendered by QuickLaTeX.com \vec{r}.\frac{1}{\sqrt3}[\hat{i} + \hat{j} + \hat{k}] = 3\sqrt{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9918de65a9d44fad49d96b1a61086493_l3.png)
or,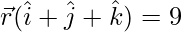
or, x + y + z = 9.
Question 9. Find the equation of the plane passing through the point (1,2,1) and perpendicular to the line joining the points (1,4,2) and (2,3,5). Find also the perpendicular distance of the origin from the plane.
Solution:
Vector equation of a plane is given by
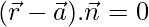 …..(1)
…..(1)
We have,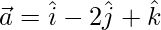
and,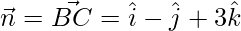
Putting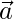 and
and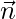 in (1), we get
in (1), we get
 ….(2)
….(2)
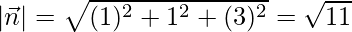
Dividing (1) by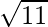
![Rendered by QuickLaTeX.com \vec{r}.[\frac{1}{\sqrt11}\hat{i} - \frac{1}{\sqrt11}\hat{j} + \frac{3}{\sqrt11}\hat{k}] = \frac{2}{\sqrt11}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8569497bb6d24ebf412b922f3cc5dcda_l3.png)
Hence, vector equation of plane is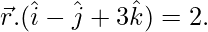
and, cartesian form is x – y + 3z – 2 = 0.
Question 10. Find the vector equation of a plane which is at a distance of from the origin and its normal vector from the origin is
from the origin and its normal vector from the origin is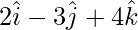 . Also, find its cartesian form.
. Also, find its cartesian form.
Solution:
Since vector equation of a plane with distance d and normal to the unit vector n is given by

Since,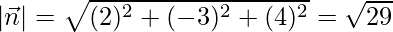
Unit vector normal to the plane =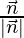
or,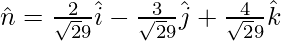

Vector equation becomes,
![Rendered by QuickLaTeX.com \vec{r}.[\frac{2}{\sqrt29}\hat{i} - \frac{3}{\sqrt29}\hat{j} + \frac{4}{\sqrt29}\hat{k}] = \frac{6}{\sqrt29}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-db738bcfaa03f36bf12e70465e426287_l3.png)
Cartesian equation is 2x – 3y + 4z = 6.
Question 11. Find the distance of the plane 2x – 3y + 4z – 6 = 0 from the origin.
Solution:
2x – 3y + 4z – 6 = 0
or, 2x – 3y + 4z = 6
Vector equation becomes,
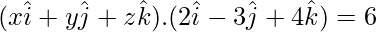
or,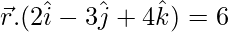 …..(1)
…..(1)
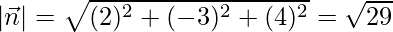
Dividing (1) by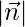 , normal form of equation becomes,
, normal form of equation becomes,
![Rendered by QuickLaTeX.com \vec{r}.[\frac{2}{\sqrt29}\hat{i} - \frac{3}{\sqrt29}\hat{j} + \frac{4}{\sqrt29}\hat{k}] = \frac{6}{\sqrt29}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-db738bcfaa03f36bf12e70465e426287_l3.png)
Hence, the perpendicular distance of the origin from the plane is units.
units.
Share your thoughts in the comments
Please Login to comment...