Class 12 RD Sharma Solutions – Chapter 24 Scalar or Dot Product – Exercise 24.1 | Set 2
Last Updated :
15 Feb, 2022
Question 17. If 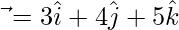 and
and 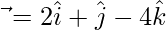 , then express
, then express  in the form of
in the form of 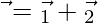 where
where 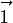 is parallel to
is parallel to  and
and 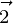 is perpendicular to
is perpendicular to  .
.
Solution:
Given, 
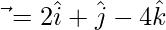
According to question
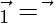 also
also 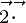 = 0
= 0
Now,
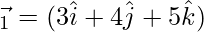
⇒ 

⇒ 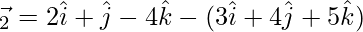
⇒ 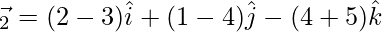
Now,

⇒ =0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c7e94f3fe677c1b535ab9a11e65e0b97_l3.png)
⇒ 3(2-3λ)+4(1-4λ)-5(4+5λ) = 0
⇒ 6-9λ+4-16λ-20-25λ = 0
⇒ -10 -50λ = 0
⇒ λ = -1/5
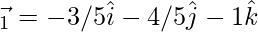

Question 18. If either 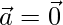 or
or 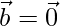 , then
, then 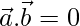 . But, The converse need not be true. Justify your answer with an example.
. But, The converse need not be true. Justify your answer with an example.
Solution:
Given,
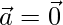 or
or 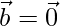 then
then 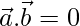
Suppose 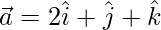
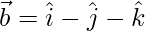
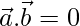
But,
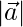 = √(2)2+(1)2+(1)2
= √(2)2+(1)2+(1)2
= √4+1+1
= √6 ≠ 0
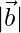 = √(1)2+(1)2+(1)2
= √(1)2+(1)2+(1)2
= √3 ≠ 0
Hence Proved
Question 19. Show that the vectors 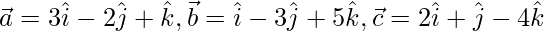 form a right-angled triangle.
form a right-angled triangle.
Solution:
Given, 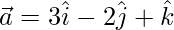
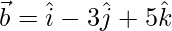
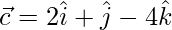
To prove given vectors form a right angle triangle
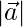 = √(32+(-2)2+12) = √14
= √(32+(-2)2+12) = √14
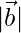 = √(12+(-3)2+52) = √35
= √(12+(-3)2+52) = √35
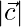 = √(22+12+(-4)2) = √21
= √(22+12+(-4)2) = √21
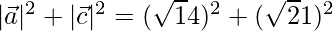
= 14 + 21 = 35
Since,  (Pythagoras Theorem)
(Pythagoras Theorem)
Hence, 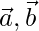 and
and 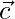 form a right angled triangle.
form a right angled triangle.
Question 20. If  ,
, 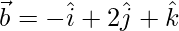 and
and 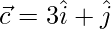 are such that
are such that 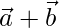 is perpendicular to
is perpendicular to 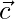 , then find the value of λ.
, then find the value of λ.
Solution:
Given:
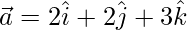
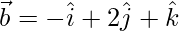
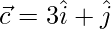
Now, 
⇒ =0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c0299ab5bffdf01a755e71fa425d0c10_l3.png)
⇒ =0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ef5e8a0ad42e56f86f3daed23b36c81_l3.png)
⇒ (2 – λ)3 + (2 + 2λ) + 0 = 0
⇒ 6 – 3λ + 2 + 2λ =0
⇒ λ = 8
Question 21. Find the angles of a triangle whose vertices are A (0, -1. -2), B (3, 1, 4), and C(5, 7, 1).
Solution:
Given that angle of a triangle whose vertices are A (0, -1. -2), B (3, 1, 4) and C(5, 7, 1).
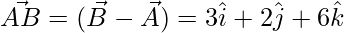
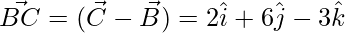

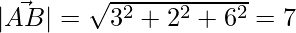
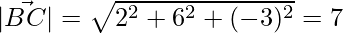
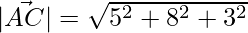
= √98 = 7√2
Now,
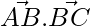 = (3 × 2 + 2 × 6 – 6 × 3) = 0
= (3 × 2 + 2 × 6 – 6 × 3) = 0
Thus, we can say AB is perpendicular to BC.
Hence, AB = BC = 7, ∠A =∠C and ∠B = 90°
∠A + ∠B + ∠C = 180°
2∠A = 180° – 90°
∠A = 45°
∠C = 45°
∠B = 90°
Question 22. Find the magnitude of two vectors 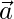 and
and 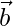 , having the same magnitude and such that the angle between them is 60° and their scalar product is 1/2.
, having the same magnitude and such that the angle between them is 60° and their scalar product is 1/2.
Solution:
We know 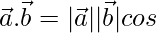
⇒ 1/ 2 = 
⇒ 1/2 = 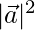 (1/2)
(1/2)
⇒ 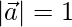
or
⇒ 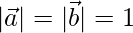
Question 23. Show that the points whose position vector are 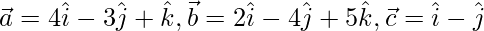 form a right triangle.
form a right triangle.
Solution:
Given that positions vectors
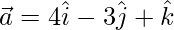

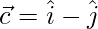
Now,
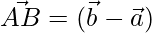
⇒ 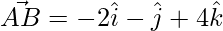
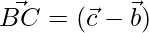
⇒ 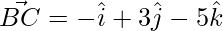

⇒ 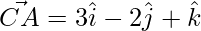
Now, 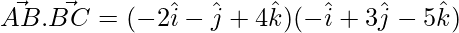
= 2 – 3 – 20 = -21
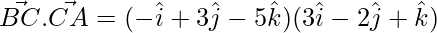
= -3 – 6 – 5 = -14

= -6 + 2 + 4 = 0
So, AB is perpendicular to CA or the given position vectors form a right-angled triangle.
Question 24. If the vertices A, B, C of △ABC have position vectors (1, 2, 3), (-1, 0, 0), (0, 1, 2) respectively, what is the magnitude of ∠ABC?
Solution:
Given the vertices of △ABC are A(1, 2, 3), B(-1, 0, 0), C(0, 1, 2)
Now, 
= 
Or, 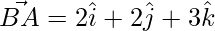
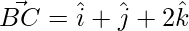
We know that 
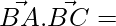 (2 × 1) + (2 × 1) + (3 × 2)
(2 × 1) + (2 × 1) + (3 × 2)
= 2 + 2 + 6 = 10
Now, 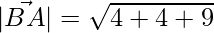 = √17
= √17
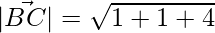 = √6
= √6
Therefore,
cos θ = 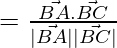
cos θ = 10/ √(17×6)
θ = cos-1(10/√102)
Question 25. If A, B, C have position vectors (0, 1, 1), (3, 1, 5), (0, 3, 3) respectively, show that △ABC is right-angled at C.
Solution:
Given, position vectors A(0, 1, 1), B(3, 1, 5), C(0, 3, 3)
Now, 
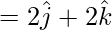

= 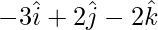
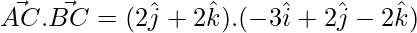
= 2 × 2 – 2 × 2 = 0
Thus, 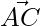 and
and 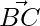 are perpendicular hence △ABC is right-angled at C
are perpendicular hence △ABC is right-angled at C
Question 26. Find the projection of  on
on  , where
, where 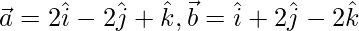 and
and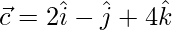 .
.
Solution:
Given:
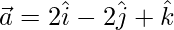
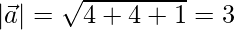
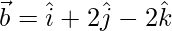
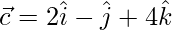
To find the projection of  on
on 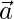

Now, Projection of  =
= ![Rendered by QuickLaTeX.com [\frac{(\vec{b}+\vec{c})\vec{a}}{|\vec{a}|^2}]\vec{a}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0906c40a1dbbb3e9e0ec49d135054a89_l3.png)
= ](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ca0053201c4f0853ce8490d189d4b08c_l3.png)
= 6/9 × 3
= 2
Question 27. If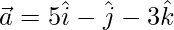 and
and 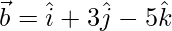 , then show that the vectors
, then show that the vectors 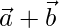 and
and 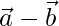 are orthogonal.
are orthogonal.
Solution:
Given: 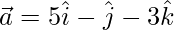
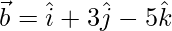
To prove
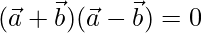
Taking LHS
= 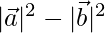
= 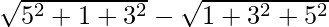
= √35 – √35
= 0
Thus, the given vectors 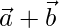 and
and 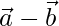 are orthogonal.
are orthogonal.
Question 28. A unit vector 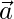 makes angle π/2 and π/3 with
makes angle π/2 and π/3 with 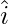 and
and 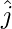 respectively and an acute angle θ with
respectively and an acute angle θ with 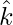 . Find the angle θ and components of
. Find the angle θ and components of  .
.
Solution:
Let us assume 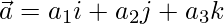
We know that
a12+ a22 + a32 = 1 ….(1)
So,
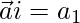
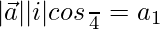
(1)(1)(1/√2) = a1
a1 = 1/√2
Again we take
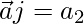

(1)(1)(1/2) = a2
a2 = 1/2
Put all these values in eq(1) to find the value of a3
(1/√2)2 + (1/2)2 + a32 = 1 ….(1)
a32 = 1/4
a3 = 1/2
Now we find the value of θ
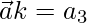
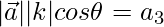
(1)(1)cosθ = 1/2
cosθ = 1/2
cosθ = π/3
and components of 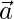
Question 29. If two vectors 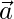 and
and 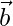 are such that
are such that 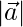 = 2,
= 2, 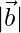 = 1, and
= 1, and 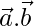 =1. Find the value of
=1. Find the value of 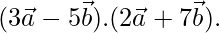
Solution:
Given, 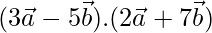
=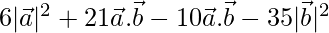
=
= 6(2)2 + 11(1) – 35(1)2
= 24 + 11 – 35
= 35 – 35 = 0
Question 30. If 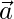 is a unit vector, then find
is a unit vector, then find 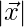 in each of the following:
in each of the following:
(i) 
Solution:
Given, 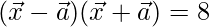
⇒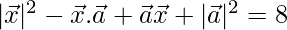
⇒ 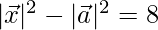
⇒ 
⇒ 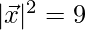
⇒
(ii) 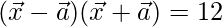
Solution:
Given, 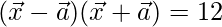
⇒ 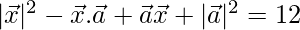
⇒ 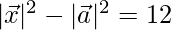
⇒ 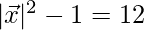
⇒ 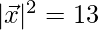
⇒ 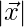 =√13
=√13
Question 31. Find 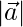 and
and 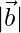 , if
, if
(i) 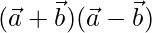 = 12 and
= 12 and 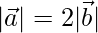
Solution:
Given, 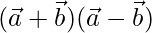 = 12
= 12
⇒ 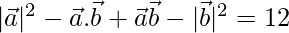
⇒ 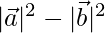 = 12
= 12
⇒ 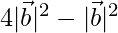 = 12
= 12
⇒ 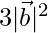 = 12
= 12
⇒ 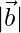 = 2
= 2
So,
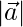 = 4
= 4
(ii) 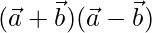 = 8 and
= 8 and 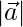 = 8
= 8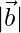
Solution:
Given, 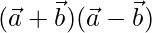 = 8
= 8
⇒ 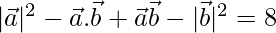
⇒ 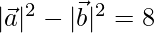
⇒
⇒ 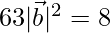
⇒ 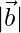 = √(8/63)
= √(8/63)
So,
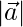 = 8√(8/63)
= 8√(8/63)
(iii) = 3 and
= 3 and 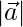 = 2
= 2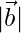
Solution:
Given, 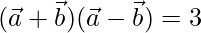
⇒ 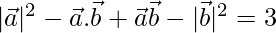
⇒ 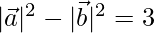
⇒ 
⇒ 3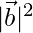 = 3
= 3
⇒ 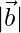 = 1
= 1
So,
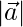 = 2
= 2
Question 32. Find  , if
, if
(i) 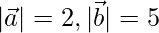 and
and 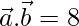
Solution:
We have, 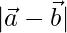
⇒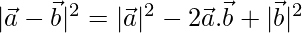
⇒ = 22 – 2 × 8 + 52
= 22 – 2 × 8 + 52
⇒  = 4 – 16 + 25
= 4 – 16 + 25
⇒  = 13
= 13
⇒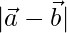 = √13
= √13
(ii) 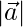 = 3,
= 3, 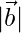 = 4 and
= 4 and 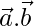 = 1
= 1
Solution:
We have, 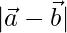
⇒ 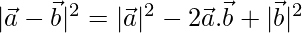
⇒ = 32 – 2 × 1 + 42
= 32 – 2 × 1 + 42
⇒ 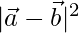 = 9 – 2 + 16
= 9 – 2 + 16
⇒  = 23
= 23
⇒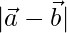 = √23
= √23
(iii)  and
and 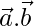 = 4
= 4
Solution:
We have, 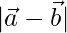
⇒ 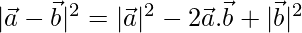
⇒ = 22 – 2 × 4 + 32
= 22 – 2 × 4 + 32
⇒  = 4 – 8 + 9
= 4 – 8 + 9
⇒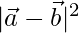 = 5
= 5
⇒  = √5
= √5
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...