Class 12 RD Sharma Solutions – Chapter 22 Differential Equations – Exercise 22.7 | Set 1
Last Updated :
05 Mar, 2021
Solve the following differential equations:
Question 1. (x – 1)(dy/dx) = 2xy
Solution:
We have,
(x – 1)(dy/dx) = 2xy
dy/y = [2x/(x – 1)]dx
On integrating both sides,
∫(dy/y) = ∫[2x + (x – 1)]dx
log(y) = ∫[2 + 2/(x – 1)]dx
log(y) = 2x + 2log(x – 1) + c (Where ‘c’ is integration constant)
Question 2. (x2 + 1)dy = xydx
Solution:
We have,
(x2 + 1)dy = xydx
(dy/y) = [x/(x2 + 1)]dx
On integrating both sides
∫(dy/y) = ∫[x/(x2 + 1)]dx
log(y) = (1/2)∫[2x/(x2 + 1)]dx
log(y) = (1/2)log(x2 + 1) + c (Where ‘c’ is integration constant)
Question 3. (dy/dx) = (ex + 1)y
Solution:
We have,
(dy/dx) = (ex + 1)y
(dy/y) = (ex + 1)dx
On integrating both sides
∫(dy/y) = ∫(ex + 1)dx
log(y) = (ex + x) + c (Where ‘c’ is integration constant)
Question 4. (x – 1)(dy/dx) = 2x3y
Solution:
We have,
(x – 1)(dy/dx) = 2x3y
(dy/y) = [2x3/(x – 1)]dx
On integrating both sides
∫(dy/y) = ∫[2x3/(x – 1)]dx
∫(dy/y) = 2∫[x2 + x + 1 + 1/(x – 1)]dx
log(y) = (2/3)(x3) + x2 + 2x + 2log(x – 1) + c (Where ‘c’ is integration constant)
Question 5. xy(y + 1)dy = (x2 + 1)dx
Solution:
We have,
xy(y + 1)dy = (x2 + 1)dx
y(y + 1)dy = [(x2 + 1)/x]dx
(y2 + y)dy = xdx + (dx/x)
On integrating both sides,
∫(y2 + y)dy = ∫xdx + (dx/x)
(y3/3) + (y2/2) = (x2/2) + log(x) + c (Where ‘c’ is integration constant)
Question 6. 5(dy/dx) = exy4
Solution:
We have,
5(dy/dx) = exy4
5(dy/y4) = ex
On integrating both sides,
5∫(dy/y4) = ∫ex
-(5/3)(1/y3) = ex + c (Where ‘c’ is integration constant)
Question 7. xcosydy = (xexlogx + ex)dx
Solution:
We have,
xcosydy = (xexlogx + ex)dx
cosydy = ex(logx + 1/x)dx
On integrating both sides,
∫cosydy = ∫ex(logx + 1/x)dx
Since, ∫[f(x) + f'(x)]exdx] = exf(x)
siny = exlogx + c (Where ‘c’ is integration constant)
Question 8. (dy/dx) = ex+y + x2ey
Solution:
We have,
(dy/dx) = ex+y + x2ey
(dy/dx) = exey + x2ey
dy = ey(ex + x2)dx
e-ydy = (ex + x2)dx
On integrating both sides,
∫e-ydy = ∫(ex + x2)dx
-e-y = ex + (x3/3) + c (Where ‘c’ is integration constant)
Question 9. x(dy/dx) + y = y2
Solution:
We have,
x(dy/dx) + y = y2
x(dy/dx) = y2 – y
[1/(y2 – y)]dy = dx/x
On integrating both sides,
∫[1/(y2 – y)]dy = ∫dx/x
∫[1/(y – 1) – 1/y]dy = ∫(dx/x)
log(y-1) – log(y) = logx + logc
log[(y – 1)/y] = log[xc]
(y – 1)/y = xc
(y-1) = yxc (Where ‘c’ is integration constant)
Question 10. (ey + 1)cosxdx + eysinxdy = 0
Solution:
We have,
(ey + 1)cosxdx + eysinxdy = 0
(cosx/sinx)dx = -[ey/(ey + 1)]dy
On integrating both sides,
∫(cosx/sinx)dx = -∫[ey/(ey + 1)]dy
log(sinx) = -log(ey + 1) + log(c)
log(sinx) + log(ey + 1) = log(c)
log[sinx(ey + 1)] = log(c)
sinx(ey + 1) = c (Where ‘c’ is integration constant)
Question 11. xcos2ydx = ycos2xdy
Solution:
We have,
xcos2ydx = ycos2xdy
(x/cos2x)dx = (y/cos2y)dy
xsec2xdx = ysec2ydy
On integrating both sides,
∫xsec2xdx = ∫ysec2ydy
![Rendered by QuickLaTeX.com x∫sec^2x - ∫[\frac{d(x)}{dx(x)}∫sec^2xdx]dx = y∫sec^2x-∫[\frac{d(y)}{dy}(y)∫sec^2y]dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6d550440c82af746174c0d8217a830cd_l3.png)
xtanx – ∫tanxdx = ytany – ∫tanydy
xtanx – log(secx) = ytany – log(secy) + c (Where ‘c’ is integration constant)
Question 12. xydy = (y – 1)(x + 1)dx
Solution:
We have,
xydy = (y – 1)(x + 1)dx
[y/(y – 1)]dy = [(x + 1)/x]dx
On integrating both sides,
∫[y/(y – 1)]dy = ∫[(x + 1)/x]dx
∫[1 + 1/(y – 1)]dy = ∫[(x + 1)/x]dx
y + log(y – 1) = x + log(x) + c
y – x = log(x) – log(y – 1) + c (Where ‘c’ is integration constant)
Question 13. x(dy/dx) + coty = 0
Solution:
We have,
x(dy/dx) + coty = 0
x(dy/dx) = -coty
dy/coty = -(dx/x)
tanydy = -(dx/x)
On integrating both sides,
∫tanydy = -∫(dx/x)
log(secy) = -log(x) + log(c)
log(secy) + log(x) = log(c)
log(xsecy) = log(c)
x/cosy = c
x = c * cosy (Where ‘c’ is integration constant)
Question 14. (dy/dx) = (xexlogx + ex)/(xcosy)
Solution:
We have,
(dy/dx) = (xexlogx + ex)/(xcosy)
xcosydy = (xexlogx + ex)dx
cosydy = ex(logx + 1/x)dx
On integrating both sides,
∫cosydy = ∫ex(logx + 1/x)dx
Since, ∫[f(x) + f'(x)]exdx] = exf(x)
siny = exlogx + c (Where ‘c’ is integration constant)
Question 15. (dy/dx) = ex+y + x3ey
Solution:
We have,
(dy/dx) = ex+y + x3ey
(dy/dx) = exey + x3ey
dy = ey(ex + x3)dx
e-ydy = (ex + x3)dx
On integrating both sides,
∫e-ydy = ∫(ex + x3)dx
-e-y = ex + (x4/4) + c
e-y + ex + (x4/4) = c (Where ‘c’ is integration constant)
Question 16. y√(1 + x2) + x√(1 + y2)(dy/dx) = 0
Solution:
We have,
y√(1 + x2) + √(1 + y2)(dy/dx) = 0
y√(1 + x2)dx = -x√(1 + y2)dy
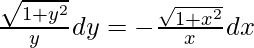
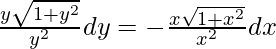
On integrating both sides,
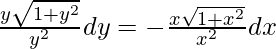
Let, 1 + y2 = z2
On differentiating both sides
2ydy = 2zdz
ydy = zdz
= 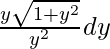
= 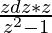
= ∫[z2/(z2 – 1)]dz
= ∫[1 + 1/(z2 – 1)]dz
= z + (1/2)log[(z – 1)/(z + 1)]
On putting the value of z in above equation
= ![Rendered by QuickLaTeX.com \sqrt{1+y^2}+\frac{1}{2}log[\frac{\sqrt{1+y^2}-1}{\sqrt{1+y^2}+1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-db0b41bd44e54c09f818b4c2f7453298_l3.png)
Similarly,
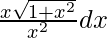 =
= ![Rendered by QuickLaTeX.com \sqrt{1+x^2}+\frac{1}{2}log[\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aa2e0f99fde2a3d6e55933e2ec7855bb_l3.png)
![Rendered by QuickLaTeX.com \sqrt{1+y^2}+\frac{1}{2}log[\frac{\sqrt{1+y^2}-1}{\sqrt{1+y^2}+1}]=-\sqrt{1+x^2}-\frac{1}{2}log[\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-988294440c9f5254c25dba1ac9ad2f2e_l3.png)
![Rendered by QuickLaTeX.com \sqrt{1+y^2}+\sqrt{1+x^2}+\frac{1}{2}log[\frac{\sqrt{1+y^2}-1}{\sqrt{1+y^2}+1}]+\frac{1}{2}log[\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}]=c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0b70ad6b84341d6d935b81c723065158_l3.png) (Where ‘c’ is integration constant)
(Where ‘c’ is integration constant)
Question 17. √(1 + x2)(dy) + √(1 + y2)dx = 0
Solution:
We have,
√(1 + x2)(dy) + √(1 + y2)dx = 0
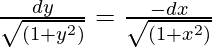
On integrating both sides,
log[y + √(1 + y2)] = -log[x + √(1 + x2)] + logc
log[y + √(1 + y2)] + log[x + √(1 + x2)] = logc
log([y + √(1 + y2)][x + √(1 + x2)]) = logc
[y + √(1 + y2)][x + √(1 + x2)] = c (Where ‘c’ is integration constant)
Question 18. 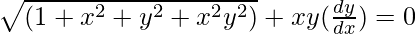
Solution:
We have,
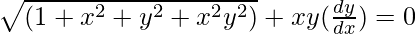
![Rendered by QuickLaTeX.com \sqrt{[(1 + x^2) + y^2(1+x^2)]}+xy(\frac{dy}{dx})=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d28474ec35a34b263f5eedf7ea904656_l3.png)
![Rendered by QuickLaTeX.com \sqrt{[(1+x^2)(1+y^2)]}+xy(\frac{dy}{dx})=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-579e07d7a4028ab7f2fa16b9159cae86_l3.png)
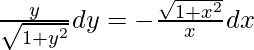
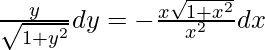
On integrating both sides,
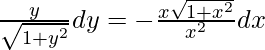
Let, 1 + x2 = z2
On differentiating both sides
2xdx = 2zdz
xdx = zdz
= 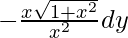
= 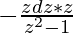
= -∫[z2/(z2 – 1)]dz
= -∫[1 + 1/(z2 – 1)]dz
= -z – (1/2)log[(z – 1)/(z + 1)]
On putting the value of z in above equation
![Rendered by QuickLaTeX.com =-\sqrt{1+x^2}-\frac{1}{2}log[\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d8c91193539915167d47cadfccbb9705_l3.png)
Let, 1 + y2 = v2
On differentiating both sides
2ydy = 2vdv
ydy = vdv
= ∫(vdv/v)
= v
On putting the value of v in above equation
= √(1 + y2)
= ![Rendered by QuickLaTeX.com \sqrt{1+y^2}=-\sqrt{1+x^2}-\frac{1}{2}log[\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6deb564ed649fa6b6062e38a19dcb198_l3.png)
= ![Rendered by QuickLaTeX.com \sqrt{1+y^2}+\sqrt{1+x^2}+\frac{1}{2}log[\frac{\sqrt{1+x^2}-1}{\sqrt{1+x^2}+1}]=c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-de796d86eed7a3a6030f9ef16c0720ab_l3.png) (Where ‘c’ is integration constant)
(Where ‘c’ is integration constant)
Question 19. 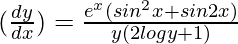
Solution:
We have,
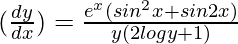
y(2logy + 1)dy = ex(sin2x + sin2x)dx
On integrating both sides,
∫y(2logy + 1)dy = ∫ex(sin2x + sin2x)dx
![Rendered by QuickLaTeX.com 2logy*∫ydy-∫[2\frac{d}{dx}(logy)∫ydy]dy+\frac{y^2}{2}=e^xsin^2x+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aba025fc07528b5baf6fd9602a97eb9f_l3.png)
Since, ∫ex(sin2x + sin2x)dx = exsin2x
Using property ∫[f(x) + f'(x)]ex = exf(x)
y2log(y) – ∫ydy + y2/2 = exsin2x + c
y2log(y) – y2/2 + y2/2 = exsin2x + c
y2log(y) = exsin2x + c (Where ‘c’ is integration constant)
Question 20. (dy/dx) = x(2logx + 1)/(siny + ycosy)
Solution:
We have,
(dy/dx) = x(2logx + 1)/(siny + ycosy)
(siny + ycosy)dy = x(2logx + 1)dx
On integrating both sides,
∫(siny + ycosy)dy = ∫x(2logx + 1)dx
∫sinydy + y∫cosydy – ∫{(dy/dy)∫cosydy}dy = 2logx∫xdx – 2∫{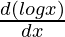 ∫xdx} + ∫xdx
∫xdx} + ∫xdx
-cosy + ysiny – ∫sinydy = x2logx – ∫xdx + (x2/2) + c
-cosy + ysiny + cosy = x2logx – (x2/2) + (x2/2) + c
ysiny = x2logx + c (Where ‘c’ is integration constant)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...