Class 12 RD Sharma Solutions – Chapter 22 Differential Equations – Exercise 22.1 | Set 2
Last Updated :
02 Aug, 2022
Determine the order and degree of the following differential equation. State also whether it is linear or non-linear(Question 14-26)
Question 14. 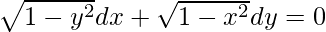
Solution:
We have,
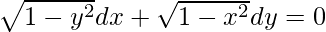
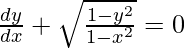
Order of function:
As the highest order of derivative of function is 1 (i.e., dy/dx)
So, the order of the derivative is equal to 1.
Degree of function:
As the power of the highest order derivative of the function is 1 (i.e., power of dy/dx is 1)
So, the degree of function is 1.
Linear or Non-linear:
The given equation is non-linear.
Question 15. 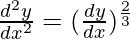
Solution:
We have,
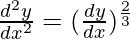
On cubing both side, we have
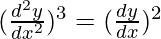
Order of function:
The Highest order of derivative of function is 2. (i.e., 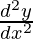 )
)
So, the order of the derivative is equal to 2.
Degree of function:
As the power of the highest order derivative of the function is 3 (i.e., power of 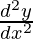 is 3)
is 3)
So, the degree of function is 3.
Linear or Non-linear:
The given equation is non-linear.
Question 16. 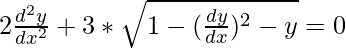
Solution:
We have,
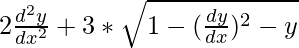
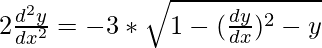
Squaring both sides, we have
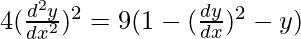
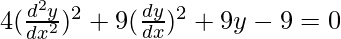
Order of function:
As the highest order of derivative of function is 2. (i.e., 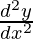 )
)
So, the order of the function is equal to 2.
Degree of function:
As the power of the highest order derivative of the function is 2 (i.e., power of 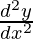 is 2)
is 2)
So, the Degree of the function is equal to 2.
Linear or Non-linear:
The given equation is non-linear.
Question 17. ![Rendered by QuickLaTeX.com 5\frac{d^2y}{dx^2}=[1+(\frac{dy}{dx})^2]^\frac{3}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-65b0146e0cf5a63c7ebc94fb0192e791_l3.png)
Solution:
We have,
![Rendered by QuickLaTeX.com 5\frac{d^2y}{dx^2}=[1+(\frac{dy}{dx})^2]^\frac{3}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-65b0146e0cf5a63c7ebc94fb0192e791_l3.png)
One squaring both side, we have
![Rendered by QuickLaTeX.com [5\frac{d^2y}{dx^2}]^2=[1+(\frac{dy}{dx})^2]^3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-269b861167681086b7b6feeb375a71da_l3.png)
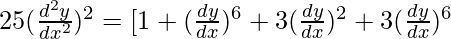
Order of function:
As the highest order of derivative of the function is 2 (i.e., 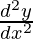 )
)
So, Order of the function is equal to 2.
Degree of function:
As the power of the highest order derivative of the function is 2 (i.e., power of 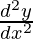 is 2)
is 2)
So, the Degree of the function is equal to 2.
Linear or Non-linear:
The given equation is non-linear.
Question 18. 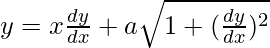
Solution:
We have,
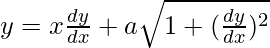
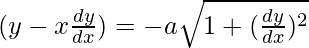
On squaring both sides, we get
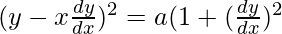
![Rendered by QuickLaTeX.com x^2(\frac{dy}{dx})^2+y^2-2xy\frac{dy}{dx}=a[1-(\frac{dy}{dx})^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9627baedb480678178390141189420d7_l3.png)
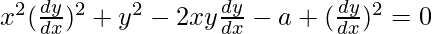
Order of function:
As the highest order of derivative of the function is 1,
So, the Order of the function is equal to 1.
Degree of function:
As the power of the highest order derivative of the function is 2.(i.e., power of dy/dx is 2)
So, the Degree of the function is equal to 2.
Linear or Non-linear:
The given equation is non-linear.
Question 19. 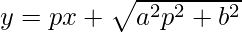 , where p = dy/dx
, where p = dy/dx
Solution:
We have
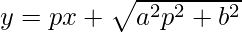 , where p = dy/dx
, where p = dy/dx
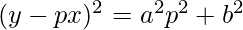
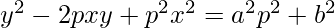
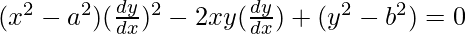
Order of function:
As the highest order of derivative of function is 1
So, the Order of the function is equal to 1.
Degree of function:
As the power of the highest order derivative of the function is 2 (i.e., power of dy/dx is 2)
So, the Degree of the function is equal to 2.
Linear or Non-linear:
The given equation is non-linear.
Question 20: dy/dx + ey = 0
Solution:
We have,
dy/dx + ey = 0
Order of function:
As the highest order of derivative of the function is 1
So, the Order of the function is equal to 1.
Degree of function:
As the power of the highest order derivative of the function is 1(i.e., power of dy/dx is 1)
So, the Degree of the function is equal to 1.
Linear or Non-linear:
The given equation is non-linear.
Question 21. 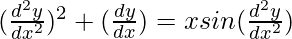
Solution:
We have,
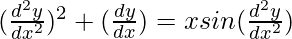
Order of function:
As the highest order of derivative of the function is 2
So, the order of the derivative is equal to 2.
Degree of function:
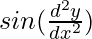 is not a polynomial function. So degree can not be defined.
is not a polynomial function. So degree can not be defined.
So, the degree of function is not defined.
Linear or Non-linear:
The given equation is non-linear.
Question 22. (y”)2 + (y’)3 + siny = 0
Solution:
We have,
(y”)2 + (y’)3 + siny = 0
Where
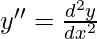
Order of function:
The highest order of derivative of the function is 2. (i.e., y”)
So, the order of the derivative is equal to 2.
Degree of function
As the power of the highest order derivative of the function is 2 (i.e., power of y” is 2)
So, the degree of function is 2.
Linear or Non-linear:
The given equation is non-linear.
Question 23.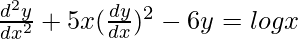
Solution:
We have,
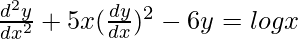
Order of function:
As the highest order of derivative of the function is 2.
So, the order of the function is equal to 2.
Degree of function:
As the power of the highest order derivative of the function is 1 (i.e., power of 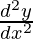 is 1)
is 1)
So, the Degree of the function is equal to 1.
Linear or Non-linear:
The given equation is non-linear.
Question 24. 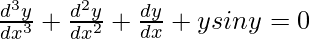
Solution:
We have,
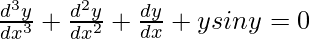
Order of function:
As the highest order of derivative of the function is 3
So, the Order of the function is equal to 3.
Degree of function:
As the power of the highest order derivative of the function is 1 (i.e., power of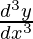 is 1)
is 1)
So, the Degree of the function is equal to 1.
Linear or Non-linear:
The given equation is linear.
Question 25. 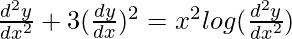
Solution:
We have,
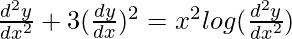
Order of function:
As the highest order of derivative of the function is 2.
So, the order of the function is equal to 2.
The degree of function:
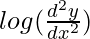 is not a polynomial function. So degree can not be defined.
is not a polynomial function. So degree can not be defined.
So, the degree of function is not defined.
Linear or Non-linear:
The given equation is non-linear.
Question 26. 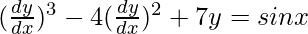
Solution:
We have,
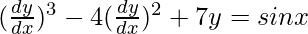
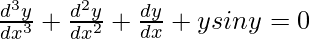
Order of function:
As the highest order of derivative of the function is 1
So, the Order of the function is equal to 1.
Degree of function:
As the power of the highest order derivative of the function is 3(i.e., power of dy/dx is 3)
So, the Degree of the function is equal to 3.
Linear or Non-linear:
The given equation is non-linear.
Share your thoughts in the comments
Please Login to comment...