Class 12 RD Sharma Solutions – Chapter 24 Scalar or Dot Product – Exercise 24.1 | Set 3
Last Updated :
28 Mar, 2021
Question 33. Find the angle between the two vectors 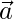 and
and 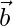 , if
, if
(i) 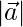 =√3,
=√3, 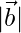 = 2 and
= 2 and 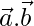 = √6
= √6
Solution:
We know, 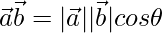
⇒ √6 = 2√3 cos θ
⇒ cos θ = 1/√2
⇒ θ = cos-1(1/√2)
⇒ θ = π/4
(ii) 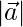 = 3,
= 3, 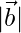 = 3 and
= 3 and 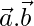 = 1
= 1
Solution:
We know, 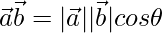
⇒ 1 = 3×3 cos θ
⇒ cos θ = 1/9
⇒ θ = cos-1(1/9)
Question 34. Express the vector 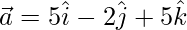 as the sum of two vectors such that one is parallel to the vector
as the sum of two vectors such that one is parallel to the vector 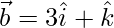 and other is perpendicular to
and other is perpendicular to 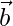
Solution:
Given, 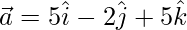
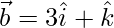
Let the two vectors be 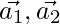
Now, 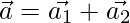 ….(1)
….(1)
Assuming 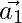 is parallel to
is parallel to 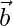
Then, 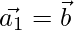 ……(2)
……(2)
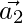 is perpendicular to
is perpendicular to 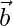
Then,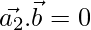 ……(3)
……(3)
From eq(1)
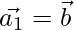
⇒ 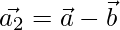
⇒ 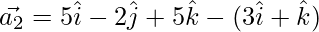
⇒ 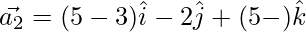
From eq(3)
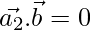
⇒ 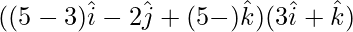
⇒ (5-3λ)3+(5-λ)=0
⇒ 15-9λ+5-λ=0
⇒ -10λ = -20
⇒ λ=2
From eq(2)
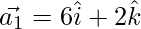
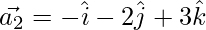
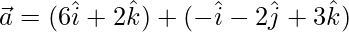
Question 35. If  and
and 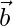 are two vectors of the same magnitude inclined at an angle of 30° such that
are two vectors of the same magnitude inclined at an angle of 30° such that 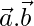 = 3, find
= 3, find 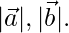
Solution:
Given that two vectors of the same magnitude inclined at an angle of 30°, and 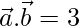
To find 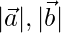
We know, 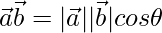
⇒ 3 = 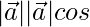
⇒ 3 = 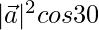
⇒ 3 = 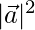 (√3/2)
(√3/2)
⇒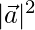 = 6/√3
= 6/√3
⇒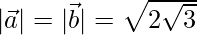
Question 36. Express 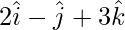 as the sum of a vector parallel and a vector perpendicular to
as the sum of a vector parallel and a vector perpendicular to 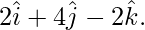
Solution:
Assuming 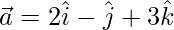
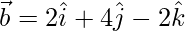
Let the two vectors be 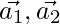
Now, 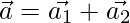
or 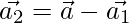 ….(1)
….(1)
Assuming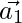 is parallel to
is parallel to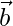
then, 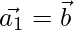 …(2)
…(2)
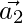 is perpendicular to
is perpendicular to 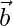
then,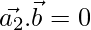 ……(3)
……(3)
Putting eq(2) in eq(1), we get
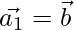
⇒ 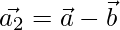
⇒ 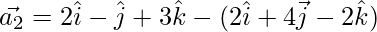
⇒ 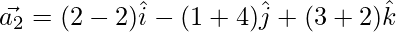
From eq(3)
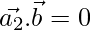
⇒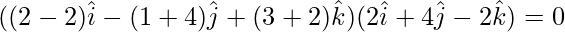
⇒ (2 – 2λ)2 – (1 + 4λ)4 – (3 + 2λ)2 = 0
⇒ 4 – 4λ – 4 – 16λ – 6 – 4λ = 0
⇒ 24λ = -6
⇒ λ = -6/24
From eq(2)
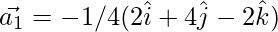
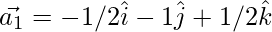
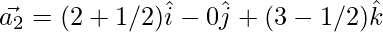
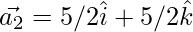
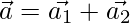
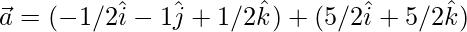
Question 37. Decompose the vector 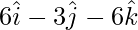 into vectors which are parallel and perpendicular to the vector
into vectors which are parallel and perpendicular to the vector 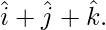
Solution:
Let 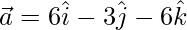 and
and 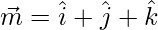
Let 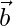 be a vector parallel to
be a vector parallel to 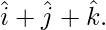
Therefore, 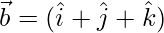
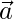 to be decomposed into two vectors
to be decomposed into two vectors
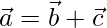
⇒ 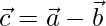
⇒ 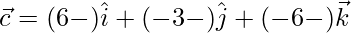
Now, 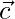 is perpendicular to
is perpendicular to 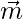
or 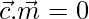
⇒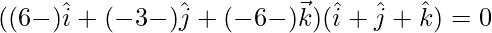
⇒ 6 – λ – 3 – λ – 6 – λ = 0
⇒ λ = -1
Therefore, the required vectors are 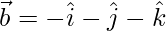 and
and 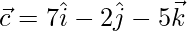
Question 38. Let 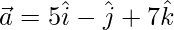 and
and 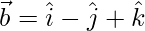 . Find λ such that
. Find λ such that 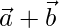 is orthogonal to
is orthogonal to 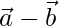
Solution:
Given, 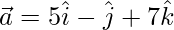
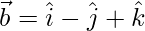
According to question
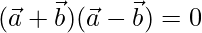
⇒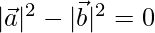
⇒ 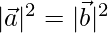
⇒ 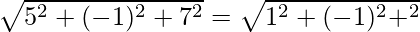
⇒ 25 + 1 + 49 = 1 + 1 + λ2
⇒ λ2 = 73
⇒ λ = √73
Question 39. If 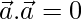 and
and 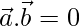 , what can you conclude about the vector
, what can you conclude about the vector 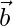 ?
?
Solution:
Given, 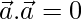 ,
,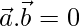
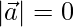
Now, 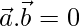
We conclude that 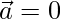 or
or 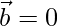 or θ = 90°
or θ = 90°
Thus, 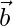 can be any arbitrary vector.
can be any arbitrary vector.
Question 40. If 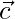 is perpendicular to both
is perpendicular to both  and
and 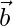 , then prove that it is perpendicular to both
, then prove that it is perpendicular to both 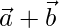 and
and 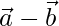
Solution:
Given 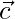 is perpendicular to both
is perpendicular to both  and
and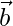
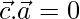 ….(1)
….(1)
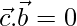 ….(2)
….(2)
To prove 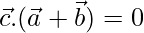 and
and 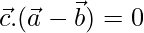
Now,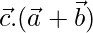
⇒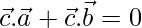 [From eq(1) and (2)]
[From eq(1) and (2)]
Again,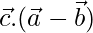
⇒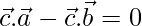 [From eq(1) and (2)]
[From eq(1) and (2)]
Hence Proved
Question 41. If 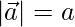 and
and 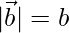 , prove that
, prove that 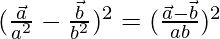
Solution:
Given, 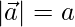 and
and 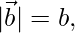
To prove
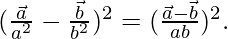
Taking LHS
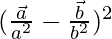
=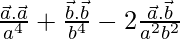
=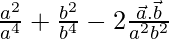
= 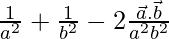
Taking RHS
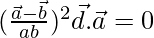
=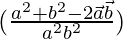
=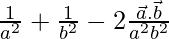
LHS = RHS
Hence Proved
Question 42. If 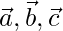 are three non- coplanar vectors such that
are three non- coplanar vectors such that 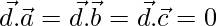 then show that
then show that 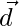 is the null vector.
is the null vector.
Solution:
Given that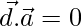
So either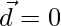 or
or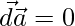
Similarly, 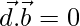
Either 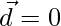 or
or 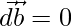
Also,
So 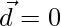 or
or 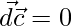
But 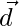 can’t be perpendicular to
can’t be perpendicular to 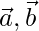 and
and 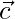 because
because 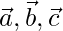 are non-coplanar.
are non-coplanar.
So 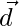 = 0 or
= 0 or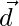 is a null vector
is a null vector
Question 43. If a vector 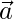 is perpendicular to two non- collinear vectors
is perpendicular to two non- collinear vectors 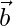 and
and 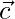 , then is
, then is 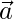 perpendicular to every vector in the plane of
perpendicular to every vector in the plane of 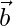 and
and 
Solution:
Given that  is perpendicular to
is perpendicular to 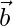 and
and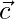
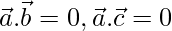
Let 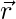 be any vector in the plane of
be any vector in the plane of 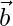 and
and 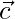 and
and 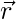 is the linear combination of
is the linear combination of 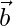 and
and 
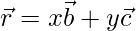 [x, y are scalars]
[x, y are scalars]
Now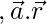
⇒ 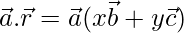
⇒ 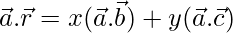
⇒ 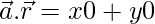
⇒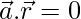
Therefore, 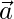 is perpendicular to
is perpendicular to 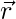 i.e.
i.e.  is perpendicular to every vector.
is perpendicular to every vector.
Question 44. If 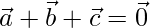 , how that the angle θ between the vectors
, how that the angle θ between the vectors 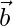 and
and 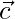 is given by cos θ =
is given by cos θ = 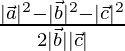
Solution:
Given that 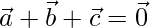
⇒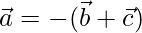
⇒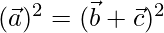
⇒ 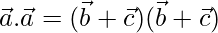
⇒ 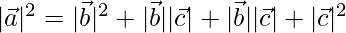
⇒ 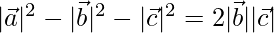
⇒ 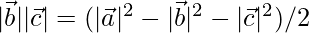
⇒ cos θ = 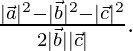
Question 45. Let 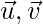 and
and 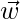 be vector such
be vector such 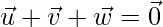 .
. 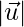 = 3,
= 3, 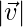 = 4 and
= 4 and 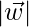 = 5, then find
= 5, then find 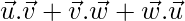
Solution:
Given that 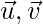 and
and 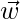 are vectors such that
are vectors such that 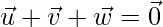 .
. 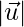 = 3,
= 3, 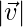 = 4 and
= 4 and 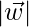 =5,
=5,
To find 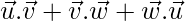
Taking
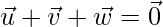
Squaring on both side, we get
⇒ 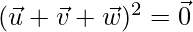
⇒ 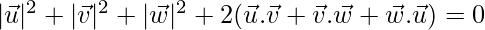
⇒ 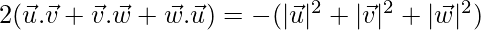
⇒ 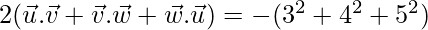
⇒ 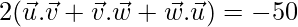
Therefore, 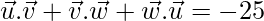
Question 46. Let 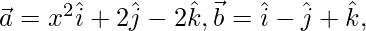 and
and 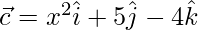 be three vectors. Find the values of x for which the angle between
be three vectors. Find the values of x for which the angle between 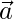 and
and 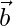 is acute and the angle between
is acute and the angle between 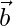 and
and 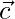 is obtuse.
is obtuse.
Solution:
Given 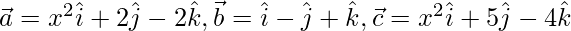
Case I: When angle between 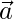 and
and 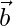 is acute:-
is acute:-
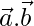 >0
>0
⇒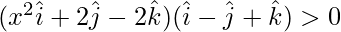
⇒ x2 – 2 – 2 > 0
⇒ x2 > 4
x ∈ (2, -2)
Case II: When angle between 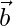 and
and 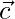 is obtuse:-
is obtuse:-
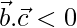
⇒ 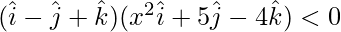
⇒ x2 – 5 – 4 < 0
⇒ x2 < 9
x ∈ (3, -3)
Therefore, x ∈ (-3, -2)∪(2, 3)
Question 47. Find the value of x and y if the vectors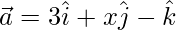 and
and 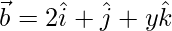 are mutually perpendicular vectors of equal magnitude.
are mutually perpendicular vectors of equal magnitude.
Solution:
Given 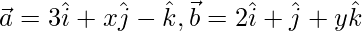 are mutually perpendicular vectors of equal magnitude.
are mutually perpendicular vectors of equal magnitude.
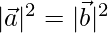
⇒ 32 + x2 + (-1)2 = 22 + 12 + y2
⇒ x2+10 = y2+5
⇒ x2 – y2 + 5 = 0 ….(1)
Now, 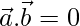
⇒ 6 + x – y = 0
⇒ y = x + 6 …..(2)
From eq(1)
x2 – (x + 6)2 + 5 = 0
⇒ x2 – (x2 + 36 – 12x) + 5 = 0
⇒ -12x – 31 = 0
⇒ x = -31/12
Now, y = -31/12 + 6
y = 41/12
Question 48. If 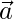 and
and 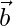 are two non-coplanar unit vectors such that
are two non-coplanar unit vectors such that 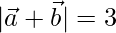 , find
, find 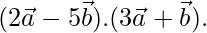
Solution:
Given that 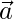 and
and 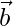 are two non-coplanar unit vectors such that
are two non-coplanar unit vectors such that 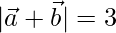
To find 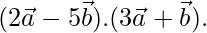
Now,
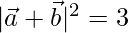
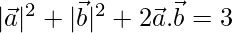
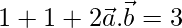
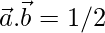
Now, 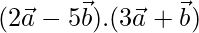
= 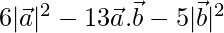
= 6 – 13(1/2) – 5
= 1 – 13/2
= -11/2
Question 49. If 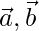 are two vectors such that |
are two vectors such that |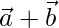 | =
| = 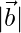 , then prove that
, then prove that 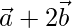 is perpendicular to
is perpendicular to 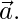
Solution:
To prove
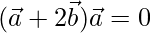
Now,
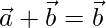
Squaring on both side, we get
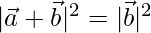
⇒ 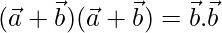
⇒ 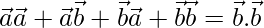
⇒ 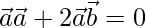
⇒ 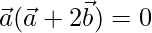
Therefore, 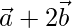 is perpendicular to
is perpendicular to 
Share your thoughts in the comments
Please Login to comment...