Class 12 RD Sharma Solutions – Chapter 23 Algebra of Vectors – Exercise 23.2

Question 1. If P, Q, and R are three collinear points such that 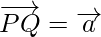 and 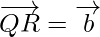.  Find the vector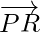 

Solution:

According to the question, given that 

Points P, Q, and R are collinear. 

Also, 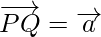and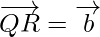 

So, 

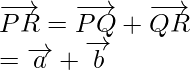
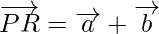
Question 2. Given condition that three vectors 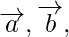 and 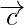 form the three sides of a triangle. What are other possibilities?

Solution:

According to the question, given that 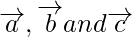are three sides of a triangle ABC.

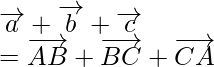
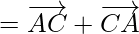        [since ]

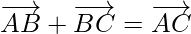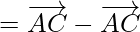             [since ]

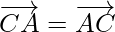So,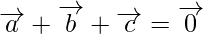 

As we know that if vectors are represented in magnitude and direction by the two sides 

of triangle taken is same order, then their sum is represented by the third side taken in reverse order.

So, 

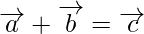
or 

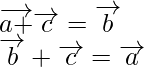
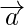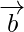Question 3. If  and  are two non- collinear vectors having the same initial point. What are the vectors represented by  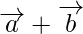and ?

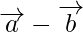Solution:

According to the question, given that 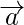and 

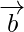
are two non-collinear vectors having the same initial point.

So, let us considered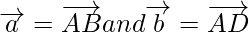 

Now we draw a parallelogram named as ABCD 

Using the properties of parallelogram, we get

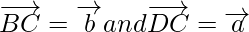
In ∆ABC,

Using the triangle law, we get

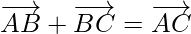
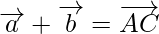…….(i)

In ∆ABD,

Using the triangle law, we get

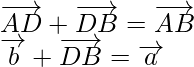
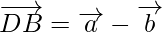…….(ii)

On solving equation (i) and (ii), we get 

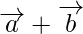 and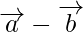 

are diagonals of a parallelogram whose adjacent sides are 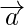 and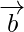 

Question 4. If 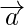 is a vector and m is a scalar such that 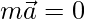, then what are the alternatives for m and ?

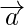Solution:

According to the question, given that m is a scalar and 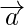 is a vector such that

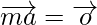
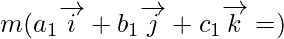                         [since let  ]

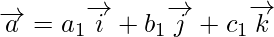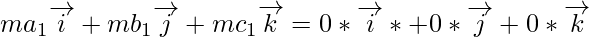
Now on comparing the coefficients of  of LHS and RHS, we get

ma₁ = 0 ⇒ m = 0 or a₁ = 0      …….(i)

mb₁ = 0 ⇒ m = 0 or b₁ = 0          …….(ii)

mc₁ = 0 ⇒ m = 0 or c₁ = 0         …….(iii)

Now from eq (i), (ii) and (iii), we get

m = 0 or a₁ = b₁ = c₁ = 0

m = 0 or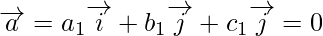 

m = 0 or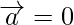 

Question 5. If 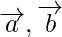 are two vectors, then write the truth value of the following statement:

(i)⇒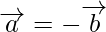

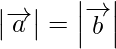
(ii)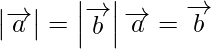

(iii)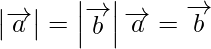

Solution:

(i) Let us assume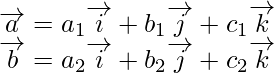

Given that, a = -b

So, 

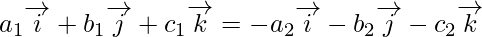
Now on comparing the coefficients of i, j, k in LHS and RHS, we get

a1 = a2         …….(i)

b1 = b2         …….(ii)

c1 = c2         …….(iii)

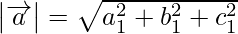
From eq(i), (ii), and (iii),

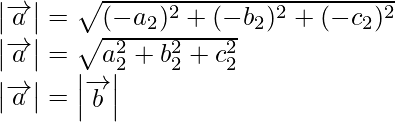
(ii) Given a and b are two vectors such that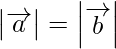

So, it means the magnitude of vector 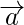is equal to the magnitude 

of vector 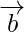, but we cannot find the direction of the vector.

Hence, it is false that

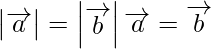
(iii) Given for any vector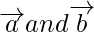

are equal but we cannot find the direction of the vector of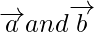 

So, it is false.

Question 6. ABCD is a quadrilateral. Find the sum of the vectors 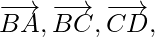 and  .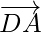

Solution:

According to the question,

ABCD is a quadrilateral.

so, 

In ∆ADC,  

By using triangle law, we get

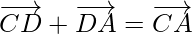……(i)

In ∆ABC, 

By using triangle law, we get

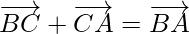 ……(ii)

Now put the value of 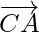in equation (ii), we get

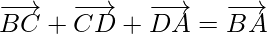
Now on adding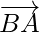on both sides,

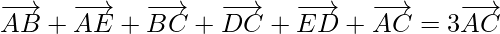
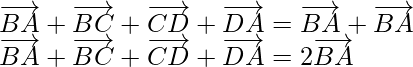
Question 7. ABCDE is a pentagon, prove that

(i)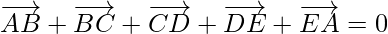

(ii)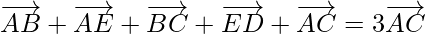

Solution:

(i) According to the question, 

ABCDE is a pentagon,

So, 

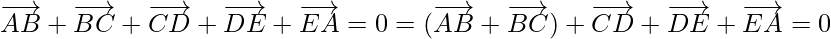
Using the law of triangle 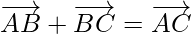, we get

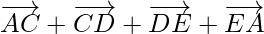
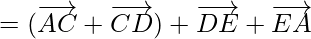
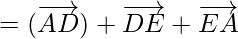
Using triangle law ,, we get

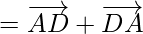
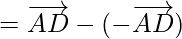
= 0

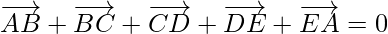
Hence Proved

(ii) According to the question, 

ABCDE is a pentagon,

So, 

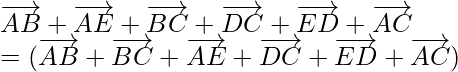
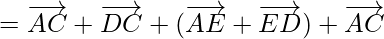
Using triangle law,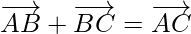, we get

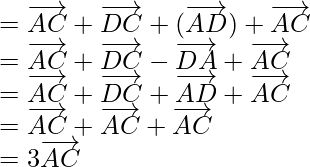
Hence Proved

Question 8. Prove that the sum of all vectors drawn from the centre of a regular octagon to its vertices is the zero vector.

Solution:

Let us assume O be the centre of a regular octagon, as we know that the 

centre of a regular octagon bisects all the diagonals passing through it.

So, 

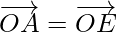   …….(i)

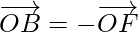  …….(ii)

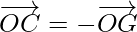 …….(iii)

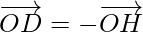[Tex]\overrightarrow{OD}=-\overrightarrow{OH}   [/Tex]     …….(iv)

Now on adding equation (i), (ii), and (iv), we get

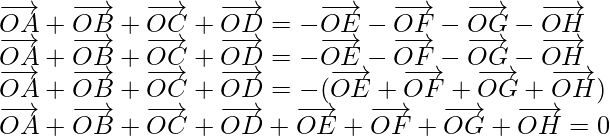
Hence proved

Question 9. If P is a point and ABCD is quadrilateral 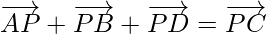 and, show that ABCD is a parallelogram.

Solution:

According to the question

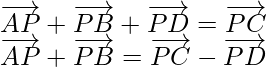
Since,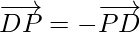 

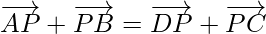
By using triangle law in ∆APB,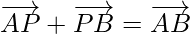 

and using triangle law in ∆ DPC,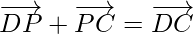 

We get

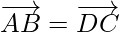
So, AB is parallel to DC and equal is magnitude.

Hence, ABCD is a parallelogram.

Question 10. Five forces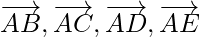 and 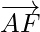 act at the vertex of a regular hexagon ABCDEF. Prove that the resultant is 6 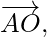where o is the centre of hexagon.

Solution:

According to the question,

Prove that

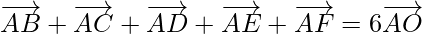
Proof:

As we know that the centre(O) of the hexagon bisects the diagonal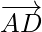 

So, 

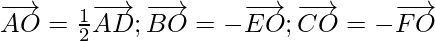
Now,

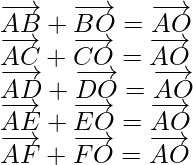
On adding these equations, we get

⇒

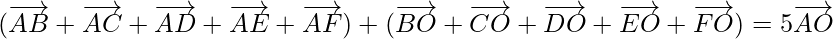
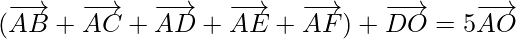
But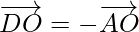 

So, 

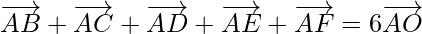
Hence proved