Question 1. Evaluate ∫ 1/√1 – cos2x dx
Solution:
Let us assume I = ∫ 1/√1 – cos2x dx
∫ 1/√1 – cos2x dx = ∫1/√2sin2x dx
= ∫ 1/(√2 sinx) dx
= (1/√2) ∫ cosec x dx
Integrate the above equation then we get
= (1/√2) log|tan x/2| + c
Hence, I = (1/√2) log|tan x/2| + c
Question 2. Evaluate ∫ 1/√1 + cos2x dx
Solution:
Let us assume I = ∫ 1/√1 + cos2x dx
∫ 1/√1 + cos2x dx = ∫1/√2cos2x/2 dx
= ∫ 1/(√2 cosx/2) dx
= (1/√2) ∫ sec x/2 dx
= (1/√2) ∫ cosec (π/2 + x/2) dx
Integrate the above equation then we get
= (2/√2) log|tan (π/4 + x/4| + c
Hence, I = √2 log|tan (π/4 + x/4| + c
Question 3. Evaluate 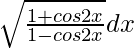
Solution:
Let us assume I = 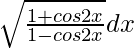
= ∫ √(2cos2x/2sin2x) dx
= ∫ √cot2x dx
= ∫ cotx dx
Integrate the above equation then we get
= log|sinx| + c [∫ cotx dx = log|sinx| + c]
Hence, I = log|sinx| + c
Question 4. Evaluate 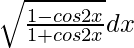
Solution:
Let us assume I = 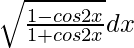
=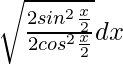
= ∫ √tan2x/2 dx
= ∫ tanx/2 dx
Integrate the above equation then we get
= -2log|cosx/2| + c [∫ tanx dx = – log|cosx| + c]
Hence, I = -2log|cosx/2| + c
Question 5. Evaluate ∫secx/sec2x dx
Solution:
Let us assume I = ∫secx/sec2x dx
∫secx/sec2x dx
= 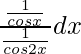
= ∫cos2x/cosx dx
= 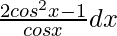
= 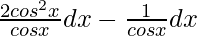
= ∫ 2cosx dx – ∫ secx dx
= 2∫ cosx dx – ∫ secx dx
Integrate the above equation then we get
= 2sinx – log|secx + tanx| + c
Hence, I = 2sinx – log|secx + tanx| + c
Question 6. Evaluate ∫ cos2x/(cosx + sinx)2 dx
Solution:
Let us assume I = ∫ cos2x/(cosx + sinx)2 dx
∫ cos2x/(cosx + sinx)2 dx
= 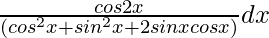
= ∫ cos2x/(1 + sin2x) dx ………….(i)
Put 1 + sin2x = t
2cos2x dx = dt
Put all these values in equation(i) then, we get
= 1/2 ∫ 1/t dt
Integrate the above equation then we get
= 1/2 log|t| + c
= 1/2 log|1 + sin2x| + c
= 1/2 log|(cosx + sinx)2| + c
Hence, I = log|sinx + cosx| + c
Question 7. Evaluate ∫ sin(x – a)/sin(x – b) dx
Solution:
Let us assume I = ∫ sin(x – a)/sin(x – b) dx
∫ sin(x – a)/sin(x – b) dx = ∫ sin(x – a + b – b)/sin(x – b) dx
= ∫ sin(x – b + b – a)/sin(x – b) dx
= 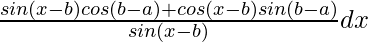
= 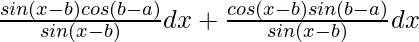
= ∫ cos(b – a) dx + ∫ cot(x – b)sin(b – a) dx
= cos(b – a) ∫dx + sin(b – a)∫ cot(x – b) dx
Integrate the above equation then we get
= xcos(b – a) + sin(b – a) log|sin(x – b)| + c
Hence, I = xcos(b – a) + sin(b – a) log|sin(x – b)| + c
Question 8. Evaluate ∫ sin(x – a)/sin(x + a) dx
Solution:
Let us assume I = ∫ sin(x – a)/sin(x + a) dx
∫ sin(x – a)/sin(x + a) dx = ∫ sin(x – a + a – a)/sin(x + a) dx
= ∫ sin(x + a – 2a)/sin(x + a) dx
= 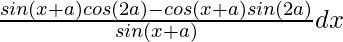
= 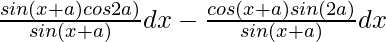
= ∫ cos(2a) dx – ∫ cot(x+a)sin(2a) dx
= cos(2a) ∫dx + sin(2a)∫ cot(x+a) dx
Integrate the above equation then we get
xcos(2a) + sin(2a) log|sin(x + a)| + c
Hence, I = xcos(2a) + sin(2a) log|sin(x + a)| + c
Question 9. Evaluate ∫ 1 + tanx/1 – tanx dx
Solution:
Let us assume I = ∫ 1 + tanx/1 – tanx dx
∫ 1 + tanx/1 – tanx dx
= 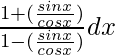
= 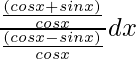
= ∫ (cosx + sinx) / (cosx – sinx) dx ………….(i)
Put cosx – sinx dx = t
(-sinx – cosx) dx = dt
– (sinx + cosx) dx = dt
dx = – dt/(sinx + cosx)
Put all these values in equation(i), we get
= – ∫dt/t
Integrate the above equation then we get
= – log|t| + c
= – log|cosx – sinx| + c
Hence, I = – log|cosx – sinx| + c
Question 10. Evaluate ∫ cosx/cos(x – a) dx
Solution:
Let us assume I = ∫ cosx/cos(x – a) dx
∫ cosx/cos(x – a) dx = ∫ cos(x + a – a)/cos(x – a) dx
= ∫ [cos(x – a)cosa – sin(x – a)sina]/cos(x – a) dx
= ∫ [cos(x – a)cosa]/cos(x – a) dx – ∫ [sin(x – a)sina]/cos(x – a) dx
= ∫ cosa dx – ∫ tan(x – a)sina dx
= cosa ∫dx – sina∫ tan(x – a) dx
Integrate the above equation then we get
= x cosa – sina log|sec(x – a)| + c
Hence, I = x cosa – sina log|sec(x – a)| + c
Question 11. Evaluate 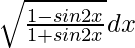
Solution:
Let us assume I = 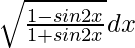
= 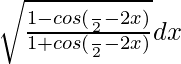
= 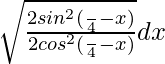
= ∫ √tan2(π/4 – x) dx
= ∫ tan(π/4 – x) dx
Integrate the above equation then we get
= log|cos(π/4 – x)| + c
Hence, I = log|cos(π/4 – x)| + c
Question 12. Evaluate ∫ e3x /(e3x + 1) dx
Solution:
Let us assume I = ∫ e3x /(e3x + 1) dx ………..(i)
Put e3x + 1 = t, then
3e3x dx = dt
dx = dt/3e3x
Put all these values in equation(i), we get
= 1/3 ∫dt/t
Integrate the above equation then, we get
= 1/3 log|t| + c
= 1/3 log |3e3x + 1| + c
Hence, I = 1/3 log |3e3x + 1| + c
Question 13. Evaluate ∫ secxtanx/3secx + 5 dx
Solution:
Let us assume I = ∫ secxtanx/3secx + 5 dx ………..(i)
Put 3secx + 5 = t
3secxtanx dx = dt
dx = dt/3secxtanx
Put all these values in equation(i), we get
= 1/3 ∫ dt/t
Integrate the above equation then, we get
= 1/3 log|t| + c
= 1/3 log|3secx + 5| + c
Hence, I = 1/3 log|3secx + 5| + c
Question 14. Evaluate ∫ 1 – cotx/1 + cotx dx
Solution:
Let us assume I = ∫ 1 – cotx/1 + cotx dx
= 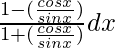
=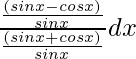
= 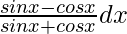 ………..(i)
………..(i)
Put sinx + cosx = t
cosx – sinx dx = dt
-(sinx – cosx) dx = dt
– dx = dt/sinx – cosx
Put all these values in equation(i), we get
= ∫ – dt/t
Integrate the above equation then, we get
= – log|t| + c
= – log|sinx + cosx| + c
Hence, I = – log|sinx + cosx| + c
Question 15. Evaluate ∫ secxcosecx/log(tanx) dx
Solution:
Let us assume I = ∫ secxcosecx/log(tanx) dx ………..(i)
log(tanx) = t
secxcosecx dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log|t| + c
= log|log(tanx)| + c
Hence, I = log|log(tanx)| + c
Question 16. Evaluate ∫1/ x(3+logx) dx
Solution:
Let us assume I = ∫1/ x(3+logx) dx ………..(i)
Let 3 + logx = t
d(3 + log x) = dt
\1/x dx = dt
dx = x dt
Putting 3 + logx =t and dx = xdt in equation (i), we get,
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log|(3 + log x)| + c
Hence, I = log|(3 + log x)| + c
Question 17. Evaluate ∫ ex + 1 / ex + x dx
Solution:
Let us assume I = ∫ ex + 1 / ex + x dx ………..(i)
Let ex + x = t
d(ex + x) = dt
(ex + 1) dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log|ex + x| + c
Hence, I = log|ex + x| + c
Question 18. Evaluate ∫1/ (xlogx) dx
Solution:
Let us assume I = ∫1/(xlogx) dx ………..(i)
Let logx = t
d(log x) = dt
1/x dx = dt
dx = x dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log|(log x)| + c
Hence, I = log|(log x)| + c
Question 19. Evaluate ∫ sin2x/ (acos2x + bsin2x) dx
Solution:
Let us assume I = ∫ sin2x/ (acos2x + bsin2x) dx ………..(i)
Let acos2x + bsin2x = t
On differentiating both side with respect to x, we get
d(acos2x + bsin2x) = dt
[a(2 cosx (-sinx)) + b(2sinxcosx)] dx = dt
[ -a (2 cosx sinx) + b(2 sinx cosx)] dx = dt
[ -a sin2x + bsin2x] dx = dt
sin2x (-a + b) dx = dt
sin2x (b – a) dx = dt
sin2x dx = dt/(b – a)
Put all these values in equation(i), we get
= 1/(b – a) ∫ dt/t
Integrate the above equation then, we get
= 1/(b – a) log |t| + c
= 1/(b – a) log|acos2x + bsin2x| + c
Hence, I = 1/(b – a) log|acos2x + bsin2x| + c
Question 20. Evaluate ∫ cosx/ 2 + 3sinx dx
Solution:
Let us assume I = ∫ cosx/ 2 + 3sinx dx ………..(i)
Let 2 + 3sinx = t
d(2 + 3sinx) = dt
3cosx dx = dt
cosx dx = dt/3
Put all these values in equation(i), we get
= 1/3 ∫ dt/t
Integrate the above equation then, we get
= 1/3 log |t| + c
= 1/3 log|2 + 3sinx| + c
Hence, I = 1/3 log|2 + 3sinx| + c
Question 21. Evaluate ∫ 1 – sinx/ x + cosx dx
Solution:
Let us assume I = ∫ 1 – sinx/ x + cosx dx ………..(i)
Let x + cosx = t
d(x + cosx) = dt
(1 – sinx) dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log|t| + c
= log|x + cosx| + c
Hence, I = log|x + cosx| + c
Question 22. Evaluate ∫ a/ b + cex dx
Solution:
Let us assume I = ∫ a/ b + cex dx
= 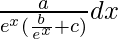
= ∫ a/ ex(be-x+c) dx ………..(i)
Let be-x + c = t
d(be-x + c) = dt
-be-x dx = dt
-b/ex dx = dt
1/ex dx = -dt/b
Put all these values in equation(i), we get
= -a/b ∫ dt/t
Integrate the above equation then, we get
= -a/b log|t| + c
= -a/b log|be-x + c| + c
Hence, I = -a/b log|be-x + c| + c
Question 23. Evaluate ∫ 1/ ex + 1 dx
Solution:
Let us assume I = ∫ 1/ ex + 1 dx
= ![Rendered by QuickLaTeX.com ∫\frac{1}{e^x[1 + \frac{1}{e^x}]} dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d7790c1affc1fb2b3926649cd5e72c6_l3.png)
= ∫ 1/ ex[1 + e-x] dx ………..(i)
Let 1 + e-x = t
d(1 + e-x) = dt
-e-x dx = dt
1/ex dx = -dt
Put all these values in equation(i), we get
= -∫ dt/t
Integrate the above equation then, we get
= -log|t| + c
= -log|1 + e-x| + c
Hence, I = -log|1 + e-x| + c
Question 24. Evaluate ∫ cotx/logsinx dx
Solution:
Let us assume I = ∫ cotx/logsinx dx ………..(i)
Let logsinx = t
d(logsinx) = dt
cosx/sinx dx = dt
cotx dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log|t| + c
= log|log sinx| + c
Hence, I = log|log sinx| + c
Question 25. Evaluate ∫ e2x / e2x – 2 dx
Solution:
Let us assume I = ∫ e2x / e2x – 2 dx ………..(i)
Let e2x – 2 = t
d(e2x – 2) = dt
e2x dx = dt
Put all these values in equation(i), we get
= 1/2 ∫ dt/t
Integrate the above equation then, we get
= 1/2 log|t| + c
= 1/2 log|e2x – 2| + c
Hence, I = 1/2 log|e2x – 2| + c
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...