Question 1. Find the image of the point (0, 0, 0) in the plane 3x + 4y – 6z + 1 = 0.
Solution:
According to the question we have
Plane = 3x + 4y – 6z + 1 = 0
Line passing through origin and perpendicular to plane is given by
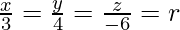
So, let the image of (0, 0, 0) = (3r, 4r, -6r)
The midpoint of (0, 0, 0) and (3r, 4r, -6r) lies on the given plane
3(3r/2) + 2(4r) – 3(-6y) + 1 = 0
30.5y = -1
r = -2/61
So, the image is (-6/61, -8/61, 12/61)
Question 2. Find the reflection of the point (1, 2, -1) in the plane 3x – 5y + 4z = 5
Solution:
According to the question we have to find the reflection of
the point P(1, 2, -1) in the plane 3x – 5y + 4z = 5
So, let Q = reflection of the point P
R = midpoint of PQ.
Then, R lies on the plane 3x – 5y + 4z = 5.
Now, the direction ratios of PQ are proportional to 3, -5, 4 and
PQ is passing through (1, 2, -1).
So, equation of PQ is,
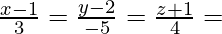
Let Q be (3λ + 1, -5λ + 2, 4λ – 1)
The coordinates of R are = 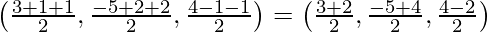
Since, R lies on the given plane i.e., 3x – 5y + 4z = 5
Therefore, 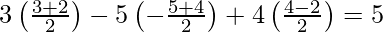
9λ + 6 + 25λ – 20 + 16λ – 8 = 10
50λ – 22 = 10
50λ = 32
λ = 16/25
Q = (3λ + 1, -5λ + 2, 4λ -1) -Equation(1)
Now, put the value of λ in equation (1), we get,
= (3(16/25)+1, -5(16/25)+2, 4(16/25)-1)
= ((48/25)+1, (-16/5)+2, (64/25)-1)
= (73/25, -6/5, 39/25)
Hence, the reflection of point (1, 2, -1) = (73/25, -6/5, 39/25)
Question 3. Find the coordinates of the foot of the perpendicular drawn from the point (5, 4, 2) to the line 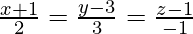 . Hence or otherwise deduce the length of the perpendicular.
. Hence or otherwise deduce the length of the perpendicular.
Solution:
According to the question we have to find foot of the perpendicular, say Q,
drawn from point P(5, 4, 2) to the line 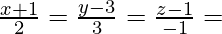
So, Let us assume Q = (2λ – 1, 3λ + 3, -λ + 1) -Equation(1)
Direction ratio of line PQ are = (2λ – 6, 3λ – 1, -λ – 1)
Here, the line PQ is perpendicular to line the given line AB
So,
a1a2 + b1b2 + c1c2 = 0
(2λ – 6)(2) + (3λ – 1)(3) + (-λ – 1)(-1) = 0
4λ – 12 + 9λ – 3 + λ + 1 = 0
14λ – 14 = 0
λ = 14/14
λ = 1
So, put the value of λ in equation(1), we get
= (2(1) – 1, 3(1) + 3, -(1) + 1)
= (2 – 1, 3 + 3, -1 +1)
= (1, 6, 0)
Now, we find the length of perpendicular PQ using distance formula
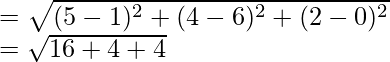
= √24
= 2√6
So, the foot of the perpendicular is (1, 6, 0)
Length of the perpendicular is 2√6 units.
Question 4. Find the image of the point with position vector 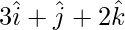 in the plane
in the plane 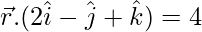 . Also find the position vector of the foot of the perpendicular and the equation of the perpendicular line through
. Also find the position vector of the foot of the perpendicular and the equation of the perpendicular line through 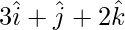 .
.
Solution:
According to the question we have to find image of the point P(3, 1, 2)
in the plane 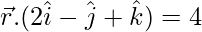 or 2x – y + z = 4.
or 2x – y + z = 4.
Let Q be the image of the point P.
So,
The direction ratios of normal to the point = 2, -1, 1
The direction ratios of line PQ perpendicular to 2, -1, 1 and
PQ is passing through (3, 1, 2)
So equation of PQ is
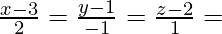
General point on the line PQ is = (2λ + 3, -λ + 1, λ + 2)
Let us assume Q = (2λ + 3, -λ + 1, λ + 2) -Equation(1)
Let R be the mid point of PQ. Then,
Coordinates of R = 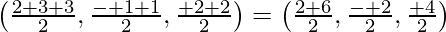
Since, R lies on the plane 2x – y + z = 4, we get
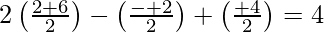
4λ + 12 + λ – 2 + λ + 4 = 8
6λ = 8 – 14
λ = -6/6
λ = -1
So, put the value of λ in equation(1), we get
Image of P = Q(2 (-1) + 3, – (-1) + 1, -1 + 2)
Image of P = (1, 2, 1)
Equation of the perpendicular line through 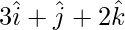 is
is
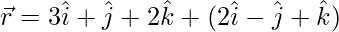
Position vector of the image point is
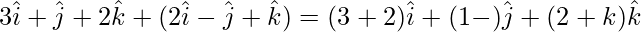
Position vector of the foot of the perpendicular is
![Rendered by QuickLaTeX.com \frac{[(3+2λ)\hat{i}+(1-λ)\hat{j}+(2+k)\hat{k}]+[3\hat{i}+\hat{j}+2\hat{k}]}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e09077a3e24fb2702d104202b5a4e642_l3.png)
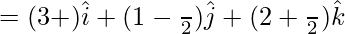
By putting the value of λ in the position vector of the foot of the perpendicular is
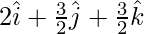
Question 5. Find the coordinates of the foot of the perpendicular from the point (1, 1, 2) to the plane 2x – 2y + 4z + 5 = 0. Also, find the length of the perpendicular.
Solution:
According to the question we have,
Plane = 2x – 2y + 4z + 5 = 0 -Equation(1)
Point = (1, 1, 2)
and find the coordinates of the foot of the perpendicular
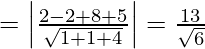
Let us assume that the foot of perpendicular = (x, y, z).
So, DR’s are in proportional
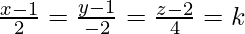
x = 2k + 1
y = -2k + 1
z = 4k + 2
Substitute (x, y, z) = (2k + 1, -2k + 1, 4k + 2) in the equation(1), we get
2x – 2y + 4z + 5 = 0
4k + 2 + 4k – 2 + 16k + 8 + 5 = 0
24k = -13
k = -13/24
So, the coordinates of the foot of the perpendicular (x, y, z) = (-1/12, 5/3, -1/6)
Question 6. Find the distance of the point (1, -2, 3) from the plane x – y + z + 5 measured along a line parallel to 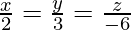
Solution:
According to the question, we have to find the distance of point P(1, -2, 3)
from the plane x – y + z = 5 measured
parallel to line AB, 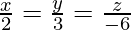
Let us assume Q = Mid point of the line joining P to plane.
We have, PQ parallel to line AB
The direction ratios of line PQ are proportional to direction ratios of line AB
The direction ratios of line PQ = 2, 3, -6
PQ is passing through point P(1, -2, 3).
Thus, the equation of PQ is,
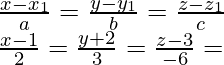
The general point on the line PQ = (2λ + 1, 3λ – 2, -6λ + 3)
Suppose the coordinates of Q = (2λ + 1, 3λ – 2, -6λ + 3)
Thus, Q lies on the plane x – y + z = 5
(2λ + 1) – (3λ – 2) + (-6λ + 3) = 5
2λ + 1 – 3λ + 2 – 6λ + 3 = 5
-7λ = -1
λ = 1/7
Coordinate of Q = (2λ + 1, 3λ – 2, -6λ + 3) -Equation(1)
Now, put the value of λ in equation(1), we get
Q = (2(1/7)+1, 3(1/7)-2, -6(1/7)+3)
Q = (9/7, -11/7, 15/7)
Now, we find the distance between (1, -2, 3) and plane = PQ
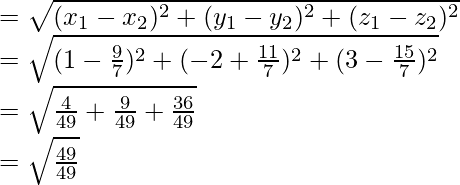
= 1
Hence, the required distance is 1 unit.
Question 7. Find the coordinates of the foot the perpendicular from the point (2, 3, 7) to the plane 3x – y – z = 7. Also, find the length of the perpendicular.
Solution:
Let us assume that Q be the foot of the perpendicular.
Now, the direction ratios of normal plane is 3, -1, -1
Line PQ is parallel to normal to plane
Direction ratios of PQ are proportional to 3, -1, -1
PQ is passing through point P(2, 3, 7)
So,
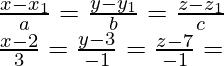
The general point on the line PQ
= (3λ + 2, -λ + 3, -λ + 7)
Coordinates of Q = (3λ + 2, -λ + 3, -λ + 7) -Equation(1)
Point Q lies on the plane 3x – y – z = 7
Thus,
3(3λ + 2) – (-λ + 3) – (-λ + 7) = 7
9λ + 6 + λ – 3 + λ – 7 = 7
11λ = 7 + 4
11λ = 11
λ = 11/11
λ = 1
Now, put the value of λ in equation(1), we get
Q = (3(1) + 2, -(1) + 3, -(1) + 7)
Q = (5, 2, 6)
Find the length of the perpendicular PQ
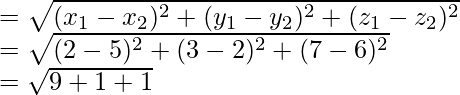
= √11
Share your thoughts in the comments
Please Login to comment...