Class 12 RD Sharma Solutions – Chapter 22 Differential Equations – Exercise 22.2 | Set 2
Last Updated :
10 May, 2021
Question 11. Assume that a raindrop evaporates at a rate proportional to its surface area. Form a differential equation involving the rate of change of the radius of the raindrop.
Solution:
Let us considered ‘r’ be the radius of rain drop, volume of the drop be ‘V’ and area of the drop be ‘A’
(dV/dt) proportional to A
(dV/dt) – kA -(V decreases with increasing in t so negative sing)
Here, k is proportionality constant,
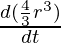 = -k(4π r2)
= -k(4π r2)
4πr2(dr/dt) = -k(4πr2)
(dr/dt) = -k
Question 12. Find the differential equation of all the parabolas with latus rectum 4a’ and whose axes are parallel to the x-axis.
Solution:
Equation of parabola whose area is parallel to x-axis and vertices at (h, k).
(y – k)2 = 4a(x – h) -(1)
On differentiating w.r.t x,
2(y – k)(dy/dx) = 4a
(y – k)(dy/dx) = 2a
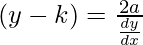 -(2)
-(2)
Again, differentiating w.r.t x,
d2y/dx2(y – k) + (dy/dx)(dy/dx) = 0
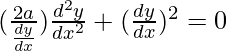
2a(d2y/dx2) + (dy/dx)3 = 0
Question 13. Show that the differential equation of which 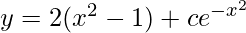 is a solution, is (dy/dx) + 2xy = 4x3
is a solution, is (dy/dx) + 2xy = 4x3
Solution:
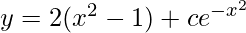 -(1)
-(1)
On differentiating w.r.t x,
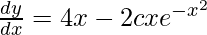
On adding 2xy in R.H.S and L.H.S,
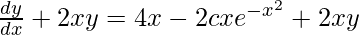
On putting the value of y in above equation,
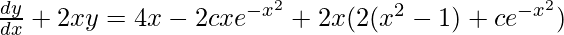
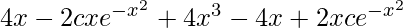 =
=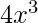
(dy/dx) + 2xy = 4x3
Question 14. From the differential equation having y = (sin-1x)2 + A cos-1x + B, where A and B are arbitrary constants, as its general solution.
Solution:
y = (sin-1x)2 + A cos-1x + B
On differentiating w.r.t x,
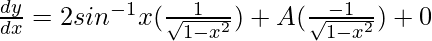
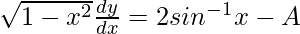
Again, on differentiating w.r.t x,
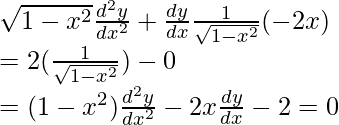
Question 15. Form the differential equation of the family of curves represented by the equation (a being the parameter)
(i) (2x + a)2 + y2 = a2
Solution:
(2x + a)2 + y2 = a2 -(1)
On differentiating w.r.t x,
2(2x + a) + 2y(dy/dx) = 0
(2x + a) + y(dy/dx) = 0
a = -2x – y(dy/dx) -(2)
On putting the value of ‘a’ in eq(1), we have
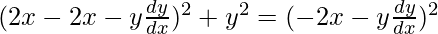
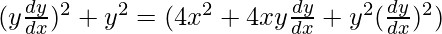
y2 = 4x2 + 4xy(dy/dx)
y2 – 4x2 – 4xy(dy/dx) = 0
(ii) (2x – a)2 – y2 = a2
Solution:
(2x – a)2 – y2 = a2
4x2 – 4ax + a2 – y2 = a2
4ax = 4x2 – y2
a = (4x2 – y2)/4x
On differentiating w.r.t x,
![Rendered by QuickLaTeX.com [\frac{4x(8x-2y\frac{dy}{dx}-4(4x^2-y^2}{(4x)^2}]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f2271fcae655de5d0e3678a7ee8a3617_l3.png)
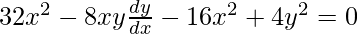
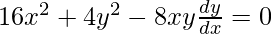
4x2 + y2 = 2xy(dy/dx)
(iii) (x – a)2 + 2y2 = a2
Solution:
(x – a)2 + 2y2 = a2 -(1)
On differentiating w.r.t x,
2(x – a) + 4y(dy/dx) = 0
(x – a) + 2y(dy/dx) = 0
a = x + 2y(dy/dx) -(2)
On putting the value of a in eq(1)
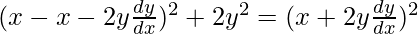
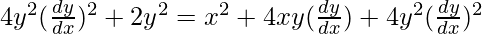
2y2 – 4xy(dy/dx) – x2 = 0
Question 16. Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
(i) x2 + y2 = a2
Solution:
x2 + y2 = a2
On differentiating w.r.t x,
2x + 2y(dy/dx) = 0
x + y(dy/dx) = 0
(ii) x2 – y2 = a2
Solution:
x2 – y2 = a2
On differentiating w.r.t x,
2x – 2y(dy/dx) = 0
x – y(dy/dx) = 0
(iii) y2 = 4ax
Solution:
y2 = 4ax
(y2/x) = 4a
On differentiating w.r.t x,
![Rendered by QuickLaTeX.com [\frac{2xy\frac{dy}{dx}-y^2}{x^2}]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2162979fa1b494d538e35a777e0bdce6_l3.png)
2xy(dy/dx) – y2 = 0
2x(dy/dx) – y = 0
(iv) x2 + (y – b)2 = 1
Solution:
x2 + (y – b)2 = 1 -(1)
On differentiating w.r.t x,
2x + 2(y – b)(dy/dx) = 0
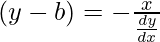
On putting the value of (y – b) in eq(1)
![Rendered by QuickLaTeX.com x^2+[-\frac{x}{\frac{dy}{dx}}]^2=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5e741966109761554bd235435fd8a0af_l3.png)
x2(dy/dx)2 + x2 = (dy/dx)2
x2[(dy/dx)2 + 1] = (dy/dx)2
(v) (x – a)2 – y2 = 1
Solution:
(x – a)2 – y2 = 1 -(1)
On differentiating w.r.t x,
2(x – a) – 2y(dy/dx) = 0
(x – a) – y(dy/dx) = 0
(x – a) = y(dy/dx)
On putting the value of (y – b) in eq(i), we get
y2(dy/dx)2 – y2 = 1
y2[(dy/dx)2 – 1] = 1
(vi)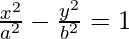
Solution:
We have,
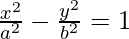 -(1)
-(1)
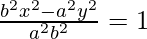
{(bx)2 – (ay)2} = (ab)2 -(2)
On differentiating w.r.t x,
2xb2 – 2a2y(dy/dx) = 0
xb2 – a2y(dy/dx) = 0 -(3)
Again, differentiating w.r.t x,
![Rendered by QuickLaTeX.com b^2-a^2[y(\frac{dy}{dx})(\frac{dy}{dx})+y\frac{d^2y}{dx^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f3698396bc96cdac95a4cd9d6e1a8f37_l3.png)
![Rendered by QuickLaTeX.com b^2=a^2[y(\frac{dy}{dx})(\frac{dy}{dx})+y\frac{d^2y}{dx^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-916c23550c41ab4bc44e047cb072b6b6_l3.png)
On putting the value of b2 in equation(3), we get
xb2 – a2y(dy/dx) = 0
![Rendered by QuickLaTeX.com xa^2[y(\frac{dy}{dx}^2)+y\frac{d^2y}{dx^2}]-a^2y\frac{dy}{dx}=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9fd6007108fd22ceeed86c1238f4a4bc_l3.png)
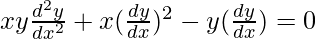
![Rendered by QuickLaTeX.com x[y\frac{d^2y}{dx^2}+(\frac{dy}{dx})^2]=y(\frac{dy}{dx})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-11349b2e0a376ecd05cac0cc747a11e0_l3.png)
(vii) y2 = 4a(x – b)
Solution:
We have,
y2 = 4a(x – b)
On differentiating w.r.t x,
2y(dy/dx) = 4a
Again differentiating w.r.t x,
![Rendered by QuickLaTeX.com 2[(\frac{dy}{dx})(\frac{dy}{dx})+y\frac{d^2y}{dx^2}]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0caa7b6e9655fb2498071a211d73e7f_l3.png)
[(dy/dx)2 + y(d2y/dx2)] = 0
(viii) y = ax3
Solution:
We have,
y = ax3 -(1)
On differentiating w.r.t x,
(dy/dx) = 3ax2
From eq(1),
a=(y/x3 -(1)
On putting the value of a in eq(1)
dy/dx = 3(y/x3) × x2
x(dy/dx) = 3y
(ix) x2 + y2 = ax3
Solution:
We have,
x2 + y2 = ax3
a = (x2 + y2)/(x3)
On differentiating w.r.t x,
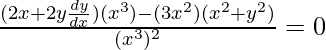
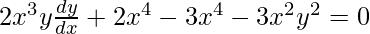
2x3y(dy/dx) = x4 + 3x2y2
2x3y(dy/dx) = x2(x2 + 3y2)
2xy(dy/dx) = (x2 + 3y2)
(x) y = eax
Solution:
We have,
y = eax -(1)
On differentiating w.r.t x,
dy/dx = aeax
dy/dx = ay -(2)
y = eax
On taking log both side, we get
logy = ax
a = (logy/x)
Now, put the value of ‘a’ in eq(2)
(dy/dx) = logy/x) × y
x(dy/dx) = ylogy
Question 17. Form the differential equation representing the family of ellipses having foci on the x-axis and the centre at the origin.
Solution:
We have,
Equation of ellipse having foci on the x-axis,
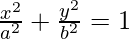 -(where a > b)
-(where a > b)
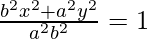
(bx)2 + (ay)2 = (ab)2 -(1)
On differentiating above equation w.r.t x,
2b2x + 2a2y(dy/dx) = 0
b2x + a2y(dy/dx) = 0 -(2)
Again, differentiating w.r.t x,
![Rendered by QuickLaTeX.com b^2+a^2[y(\frac{dy}{dx})(\frac{dy}{dx})+y\frac{d^2y}{dx^2}]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cf7aa4a41a123e93fdef4b813726ff70_l3.png)
![Rendered by QuickLaTeX.com b^2=-a^2[y(\frac{dy}{dx})(\frac{dy}{dx})+y\frac{d^2y}{dx^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a0d2b9dbd418bb7643d9b6a490e7e328_l3.png)
On putting the value of b2 in eq(2),
xb2 + a2y(dy/dx) = 0
![Rendered by QuickLaTeX.com -xa^2[y(\frac{dy}{dx}^2)+y\frac{d^2y}{dx^2}]+a^2y\frac{dy}{dx}=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc6e385e7dacc762c82194be90873992_l3.png)
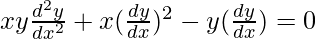
x[y(d2y/dx2) + (dy/dx)2] = y(dy/dx)
Question 18. Form the differential equation of the family of hyperbolas having foci on the X-axis and centre at the origin
Solution:
We have,
Equation of a hyperbola having a Centre at the origin and foci along x-axis
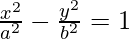 -(1)
-(1)
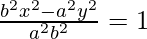
(bx)2-(ay)2=(ab)2 -(2)
On differentiating above equation w.r.t x,
2xb2-2a2y(dy/dx)=0
xb2-a2y(dy/dx)=0 -(3)
Again, differentiating above equation w.r.t x,
![Rendered by QuickLaTeX.com b^2-a^2[y(\frac{dy}{dx})(\frac{dy}{dx})+y\frac{d^2y}{dx^2}]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac7e359b5ace99aad47d6a7440af2654_l3.png)
![Rendered by QuickLaTeX.com b^2=a^2[y(\frac{dy}{dx})(\frac{dy}{dx})+y\frac{d^2y}{dx^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-916c23550c41ab4bc44e047cb072b6b6_l3.png)
Putting the value of b2 in equation(3),
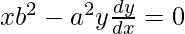
![Rendered by QuickLaTeX.com xa^2[y(\frac{dy}{dx}^2)+y\frac{d^2y}{dx^2}]-a^2y\frac{dy}{dx}=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9fd6007108fd22ceeed86c1238f4a4bc_l3.png)
xy(d2y/dx2) + x(dy/dx)2 – y(dy/dx) = 0
x[y(d2y/dx2) +(dy/dx)2] = y(dy/dx)
This is required differential equation.
Question 19. Form the differential equation of the family of circles in the second quadrant and touching the coordinate axis.
Solution:
We have,
Let (-a, a) be the coordinates of the centre of circle
So, the equation of circle is given by,
(x + a)2 + (y – b)2 = a2 -(1)
x2 + 2ax + a2 + y2 – 2ay + a2 = 0 -(2)
On differentiating above equation w.r.t x,
2x + 2a + 2y(dy/dx) – 2a(dy/dx) = 0
x + a + y(dy/dx) – a(dy/dx) = 0
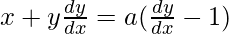
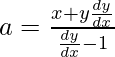
On substituting the value of ‘a’ in eq(2)
![Rendered by QuickLaTeX.com [x+\frac{x+y\frac{dy}{dx}}{\frac{dy}{dx}-1}]^2+[y-\frac{x+y\frac{dy}{dx}}{\frac{dy}{dx}-1}]^2=[\frac{x+y\frac{dy}{dx}}{\frac{dy}{dx}-1}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d5cd8005a33cca3d1400ae42d9011cd_l3.png)
Let, (dy/dx) = p
[xp – x + x + yp]2 + [yp – y – x – yp]2 = [x + yp]2
(x + y)2p2 + (x + y)2 = (x + yp)2
(x + y)2[p2 + 1] = (x + yp)2 -(where (dy/dx) = p)
Share your thoughts in the comments
Please Login to comment...