Question 15. A dice is thrown thrice. A success is 1 or 6 in a throw. Find the mean and variance of the number of successes.
Solution:
Let p denote the success and q denote failure of an event.
Now, the sample space when a dice is thrown is given by S = {1, 2, 3, 4, 5, 6}
Hence, p = 2/6 = 1/3 and q = 1 – 1/3 = 2/3
Therefore, Mean = np = 3 × 1/3 = 1 and Variance = npq = 1 × 2/3 = 2/3
Question 16. If a random variable X follows a binomial distribution with mean 3 and variance 3/2, find P (X ≤ 5).
Solution:
We are given mean (np) = 3 and variance (npq) = 3/2.
Solving for the value of q, 
q = 1/2, hence we can conclude p = 1 – 1/2 = 1/2
Now putting the value of p in relation, np = 3, we get n = 6
We know that a binomial distribution follows the relation:
P(X = r) = nCr pr(q)n-r
Therefore, in this case P(X = r) = 6Cr (1/2)r(1/2)6-r
P(X = r) = 6Cr (1/2)6
We are required to calculate the value for P(X ≤ 5) = 1 – P(X = 6)
P(X ≤ 5) = 1 – 6Cr (1/2)6
P(X ≤ 5) = 1 – (1/64)
P(X ≤ 5) = 63/64
Question 17. If X follows a binomial distribution with mean 4 and variance 2, find P(X ≥ 5).
Solution:
We are given mean (np) = 4 and variance (npq) = 2.
Solving for the value of q, npq/np = 2/4
q = 1/2, hence we can conclude p = 1 – 1/2 = 1/2
Now putting the value of p in relation, np = 4, we get n = 8
We know that a binomial distribution follows the relation: P(X = r) = nCr pr(q)n-r
Therefore, in this case P(X = r) = 8Cr (1/2)r(1/2)8-r
P(X = r) = 8Cr (1/2)8
We are required to calculate the value
P(X ≥ 5) = P(X = 5) + P(X = 6) + P(X = 7) + P(X = 8)
P(X ≥ 5) = 8C5 (1/2)8 + 8C6 (1/2)8 + 8C7 (1/2)8 + 8C8 (1/2)8
P(X ≥ 5) = (1/2)8[8C5 + 8C6 + 8C7 + 8C8]
P(X ≥ 5) = (56 + 28 + 8 + 1)/256
P(X ≥ 5) = 93/256
Question 18. The mean and variance of a binomial distribution are 4/3 and 8/9 respectively. Find P(X ≥ 1).
Solution:
We are given mean (np) = 4 and variance (npq) = 2
Solving for the value of q, npq/np = 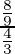
q = 2/3, hence we can conclude p = 1 – 2/3 = 1/3
Now putting the value of p in relation, np = 4/3, we get n = 4
We know that a binomial distribution follows the relation: P(X = r) = nCr pr(q)n-r
Therefore, in this case P(X = r) = 4Cr (1/3)r(2/3)4-r
We are required to calculate the value for P(X ≥ 1) = 1 – P(X = 0)
P(X ≥ 1) = 1 – 4C0 (1/3)0(2/3)4
P(X ≥ 1) = 1 – 16/81
P(X ≥ 1) = 65/81
Question 19. If the sum of the mean and variance of a binomial distribution for 6 trials is 10/3, find the distribution.
Solution:
Given n = 6 and np + npq = 10/3
np (1 + q) = 10/3
6p (1 + 1 – p) = 10/3
12p – 6p2 = 10/3
18p2 – 36p + 10 = 0
Solving for the value of p we will get p = 1/3 or p = 5/3.
Since, the value of p cannot exceed 1, we will consider p = 1/3.
Therefore, q = 1 – 1/3 = 2/3
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 6Cr (1/3)r(2/3)6-r for r = 0,1,2,….,6
Question 20. A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability distribution of the number of successes and, hence, find its mean.
Solution:
We are given n = 4 and
a doublet in the throw of a dice occurs when we get (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)
Therefore, the probability of success, p = 6/36 = 1/6, so q = 1 – 1/6 = 5/6
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 4Cr (1/6)r(5/6)4-r for r = 0, 1, 2, 3, 4
Hence, the probability distribution is given as:
X
| 0
| 1
| 2
| 3
| 4
|
|---|
| P(X) | 625/1296 | 500/1296 | 150/1296 | 20/1296 | 1/1296 |
Mean = 0 × (625/1296) + 1 × (500/1296) + 2 × (150/1296) + 3 × (20/1296) + 0 × (1/1296)
= 864/ 1296
= 2/3
Question 21. Find the probability distribution of the number of doublets in three throws of a pair of dice and find its mean.
Solution:
We are given n = 3 and
a doublet in the throw of a dice occurs when we get (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)
Therefore, the probability of success, p = 6/36 = 1/6, so q = 1 – 1/6 = 5/6
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 3Cr (1/6)r(5/6)3-r for r = 0, 1, 2, 3
Hence, the probability distribution is given as:
X
| 0
| 1
| 2
| 3
|
|---|
| P(X) | 125/216 | 75/216 | 15/216 | 1/216 |
Mean = 0 × (125/216) + 1 × (75/216) + 2 × (15/216) + 3 × (1/216)
= 108/216
= 1/2
Question 22. From a lot of 15 bulbs which include 5 defective, a sample of 4 bulbs is drawn one by one with replacement. Find the probability distribution of number of defective bulbs. Hence, find the mean of the distribution.
Solution:
Total number of bulbs = 15 and total defective bulbs = 5
Thus, the probability of getting one defective bulb with replacement, p = 5/15 = 1/3
Hence, q = 1 – 1/3 = 2/3.
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 4Cr (1/3)r(2/3)4-r for r = 0, 1, 2, 3, 4
Hence, the probability distribution is given as:
X
| 0
| 1
| 2
| 3
| 4
|
|---|
| P(X) | 16/81 | 32/81 | 24/81 | 8/81 | 1/81 |
Mean = 0 × (16/81) + 1 × (32/81) + 2 × (24/81) + 3 × (8/81) + 4 × (1/81)
= 108/81
= 4/3
Question 23. A die is thrown three times. Let X be ‘the number of twos seen’. Find the expectation of X.
Solution:
We are given the number of throws, n = 3
Let p denote the probability of getting a 2 in the throw of a dice, then p = 1/6
Therefore, we can conclude 1 = 1 – 1/6 = 5/6
Now, the expectation of X denotes mean therefore, E(X) = np = 3 × 1/6 = 1/2
Question 24. A die is tossed twice. A ‘success’ is getting an even number on a toss. Find the variance of the number of successes.
Solution:
We are given the number of times the coin is tossed, n = 2
Let p denote the probability of getting even number on dice upon throwing which is a success.
Thus, p = 3/6 = 1/2, therefore we can conclude q = 1 – p = 1 – 1/2 = 1/2
Now, the variance is given by npq.
Variance = 2 × 1/2 × 1/2 = 1/2
Question 25. Three cards are drawn successively with replacement from a well-shuffled pack of 52 cards. Find the probability distribution of the number of spades. Hence, find the mean of the distribution.
Solution:
Number of cards drawn with replacement, n = 3
p = Probability of getting a spade card upon withdrawal = 13/52 = 1/4
Thus, we can conclude, q = 1 – 1/4 = 3/4
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 3Cr (1/4)r(3/4)3-r for r = 0, 1, 2, 3
Hence, the probability distribution is given as:
X
| 0
| 1
| 2
| 3
|
|---|
| P(X) | 27/64 | 27/64 | 9/64 | 1/64 |
Mean = 0 × (27/64) + 1 × (27/64) + 2 × (9/64) + 3 × (1/64)
= (27 + 18 + 3)/64
= 48/64
= 3/4
Question 26. An urn contains 3 white and 6 red balls. Four balls are drawn one by one with replacement from the urn. Find the probability distribution of the number of red balls drawn. Also, find mean and variance of the distribution.
Solution:
Let p denote the probability of drawing a red ball which is considered a success, p = 6/9 = 2/3
And the probability of drawing a white ball which is considered a failure, q = 3/9 = 1/3
We have to draw four balls, so n = 4.
Hence, the mean of the probability distribution = np = 4 × 2/3 = 8/3
And variance = npq = 8/3 × 1/3 = 8/9
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 4Cr (2/3)r(1/3)4-r for r = 0, 1, 2, 3, 4
Hence, the probability distribution is given as:
X
| 0
| 1
| 2
| 3
| 4
|
|---|
| P(X) | 1/81 | 8/81 | 24/81 | 32/81 | 16/81 |
Question 27. Five bad oranges are accidentally mixed with 20 good ones. If four oranges are drawn one by one successively with replacement, then find the probability distribution of number of bad oranges drawn. Hence, find the mean and variance of the distribution.
Solution:
Let p denote the probability of drawing a bad orange which is considered a success, p = 5/25 = 1/5
And the probability of drawing a good orange which is considered a failure, q = 20/25 = 4/5
We have to draw four oranges, so n = 4
Hence, the mean of the probability distribution = np = 4 × 1/5 = 4/5
And the variance = npq = 4/5 × 4/5 = 16/25
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 4Cr (1/5)r(4/5)4-r for r = 0, 1, 2, 3, 4
Hence, the probability distribution is given as:
X
| 0
| 1
| 2
| 3
| 4
|
|---|
| P(X) | 256/625 | 256/625 | 96/625 | 16/625 | 1/625 |
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...