Question 1. Maximize Z = 5x + 2y,
Subject to
3x + 5y ≤ 15
5x + 2y ≤ 10
x, y ≥ 0
Solution:
Convert the given in equations into equations,
We will get the following equations:
3x + 5y = 15,
5x + 2y = 10,
x = 0 and
y = 0
Area represented by 3x + 5y ≤ 15:
The line 3x + 5y = 15 connects the coordinate axes at A(5,0) and B(0,3) respectively.
By connecting these points we will get the line 3x + 5y = 15.
Thus,
(0,0) assure the in equation 3x + 5y ≤ 15.
Hence,
The area having the origin shows the solution set of the in equation 3x + 5y ≤ 15.
Area shows by 5x + 2y ≤ 10:
The line 5x + 2y = 10 connects the coordinate axes at C(2,0) and D(0,5) respectively.
By connecting these points we will get the line 5x + 2y = 10.
Thus,
(0,0) satisfies the in equation 5x + 2y ≤ 10.
Hence,
The area having the origin shows the solution set of the in equation 5x + 2y ≤ 10.
Area shows by x ≥ 0 and y ≥ 0:
Here,
All the point in the first quadrant assures these in equations.
Thus,
The first quadrant is the area shows by the in equations x ≥ 0, and y ≥ 0.
The feasible area determined by the system of constraints, 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, and y ≥ 0, are as follows.

The corner points of the feasible area are O(0, 0), C(2, 0), E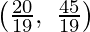 and B(0, 3).
and B(0, 3).
The values of Z at these corner points are as follows.
Corner point
| Z = 5x + 3y
|
O(0, 0)
| 5 × 0 + 3 × 0 = 0
|
C(2, 0)
| 5 × 2 + 3 × 0 = 10
|
E 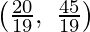
| 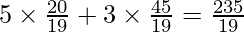
|
B(0, 3)
| 5 × 0 + 3 × 3 = 9
|
Hence,
The maximum value of Z
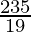 at the point
at the point 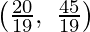
Hence,
x= 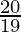 and y =
and y = 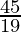 is the best solution of the given LPP.
is the best solution of the given LPP.
Therefore,
The best value of Z is 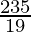 .
.
Question 2. Maximize Z = 9x + 3y
Subject to
2x + 3y ≤ 13
3x + y ≤ 5
x, y ≥ 0
Solution:
Convert the given in equations into equations,
We will get the following equations:
2x + 3y = 13,
3x +y = 5,
x = 0 and
y = 0
Area shown by 2x + 3y ≤ 13:
The line 2x + 3y = 13 connects the coordinate axes at A 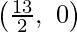 and B
and B 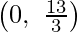 respectively.
respectively.
By connecting these points we will get the line 2x + 3y = 13.
Thus,
(0,0) assures the line equation 2x + 3y ≤ 13.
Thus, the area showing the origin represents the solution set of the in equation 2x + 3y ≤ 13.
The area shows by 3x + y ≤ 5:
The line 5x + 2y = 10 connects the coordinate axes at C 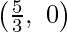 and D(0, 5) respectively.
and D(0, 5) respectively.
After connecting these points,
We will get the line 3x + y = 5.
Thus,
(0,0) assures the in equation 3x + y ≤ 5.
Thus,
The area having the origin represents the solution set of the in equation 3x + y ≤ 5.
Area shown by x ≥ 0 and y ≥ 0:
Hence,
All the point in the first quadrant assures these in equations.
Thus,
The first quadrant is the area shown by the in equations x ≥ 0, and y ≥ 0.
The suitable area determined by the system of constraints,
2x + 3y ≤ 13,
3x + y ≤ 5,
x ≥ 0, and
y ≥ 0, are as follows.

The corner points of the suitable area are O(0, 0), C 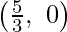 , E
, E 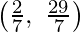 and B
and B 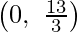 .
.
The values of Z at these corner points are as follows.
Corner point
| Z = 9x + 3y
|
O(0, 0)
| 9 × 0 + 3 × 0 = 0
|
C 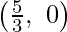
| 9 × 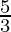 + 3 × 0 = 15 + 3 × 0 = 15
|
E 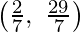
| 9 × 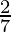 + 3 × + 3 × 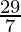 = 15 = 15
|
B 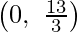
| 9 × 0 + 3 ×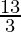 = 13 = 13
|
Here,
We can see that the maximum value of the objective function Z is 15 which is at C 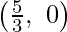 and E
and E 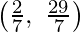 .
.
Thus,
The best value of Z is 15.
Question 3. Minimize Z = 18x + 10y
Subject to
4x + y ≥ 20
2x + 3y ≥ 30
x, y ≥ 0
Solution:
Convert the given in equations into equations,
We will get the following equations:
4x + y = 20,
2x +3y = 30,
x = 0 and
y = 0
Area shown by 4x + y ≥ 20 :
The line 4x + y = 20 connects the coordinate axes at A(5, 0) and B(0, 20) respectively.
By connecting these points we will get the line 4x + y = 20.
Thus,
(0,0) does not assure the in equation 4x + y ≥ 20.
Thus,
The area in xy plane which does not have the origin represents the solution set of the in equation 4x + y ≥ 20.
Area shown by 2x +3y ≥ 30:
The line 2x +3y = 30 connects the coordinate axes at C(15,0) and D(0, 10) respectively.
By joining these points we will get the line 2x +3y = 30.
Thus, (0,0) does not assure the in equation 2x +3y ≥ 30.
Thus,
The area which does not have the origin shows the solution set of the in equation 2x +3y ≥ 30.
Area shown by x ≥ 0 and y ≥ 0:
Hence,
Every point in the first quadrant assure these in equations.
Thus,
The first quadrant is the area shown by the in equations x ≥ 0, and y ≥ 0.
The suitable area determined by the system of constraints, 4x + y ≥ 20, 2x +3y ≥ 30, x ≥ 0, and y ≥ 0, are as follows.

The corner points of the suitable area are
B(0, 20),
C(15,0),
E(3,8) and
C(15,0).
The values of Z at these corner points are as follows.
Corner point
| Z = 18x + 10y
|
B(0, 20)
| 18 × 0 + 10 × 20 = 200
|
E(3,8)
| 18 × 3 + 10 × 8 = 134
|
C(15,0)
| 18 × 15 + 10 ×0 = 270
|
Hence,
The minimum value of Z is 134 at the point E(3,8). Hence, x = 3 and y =8 is the best solution of the given LPP.
Therefore,
The best value of Z is 134.
Question 4. Maximize Z = 50x + 30y
Subject to
2x + y ≤ 18
3x + 2y ≤ 34
x, y ≥ 0
Solution:
Convert the given in equations into equations,
We will get the following equations:
2x + y = 18, 3x + 2y = 34
The area shown by 2x + y ≥ 18:
The line 2x + y = 18 connects the coordinate axes at A(9, 0) and B(0, 18) respectively.
After connecting these points
We will get the line 2x + y = 18.
Thus,
(0,0) does not assure the in equation 2x + y ≥ 18.
Thus,
The region in xy plane which does not have the origin represents the solution set of the in equation 2x + y ≥ 18.
The area shown by 3x + 2y ≤ 34:
The line 3x + 2y = 34 connects the coordinate axes at C 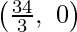 , 0 and D(0, 17) respectively.
, 0 and D(0, 17) respectively.
After joining these points we will get the line 3x + 2y = 34.
Thus,
(0,0) assure the in equation 3x + 2y ≤ 34.
Thus,
The area having the origin shows the solution set of the in equation 3x + 2y ≤ 34.
The corner points of the suitable area are
A(9, 0), C 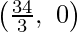 and E(2, 14).
and E(2, 14).

The values of Z at these corner points are as follows.
Corner point
| Z = 50x + 30y
|
A(9, 0)
| 50 × 9 + 3 × 0 = 450
|
C 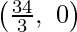
| 50 × 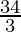 + 30 × 0 = + 30 × 0 = 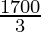
|
E(2, 14)
| 50 × 2 + 30 × 14 = 520
|
Hence,
The maximum value of Z is 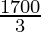 at the point
at the point 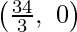 .
.
Hence,
x = 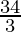 and y = 0 is the best solution of the given LPP.
and y = 0 is the best solution of the given LPP.
Therefore,
The best value of Z is 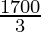
Question 5. Maximize Z = 4x + 3y
Subject to
3x + 4y ≤ 24
8x + 6y ≤ 48
x ≤ 5
y ≤ 6
x, y ≥ 0
Solution:
Here we have to maximize Z = 4x + 3y
Convert the given in equations into equations,
We will get the following equations:
3x + 4y = 24,
8x + 6y = 48,
x = 5,
y = 6,
x = 0 and
y = 0.
The line 3x + 4y = 24 connects the coordinate axis at A(8, 0) and B(0,6).
Connect these points to get the line 3x + 4y = 24.
Thus,
(0, 0) assure the in equation 3x + 4y ≤ 24.
Thus,
The area in xy-plane that have the origin showing the solution set of the given equation.
The line 8x + 6y = 48 connects the coordinate axis at C(6, 0) and D(0,8). Connect these points to get the line 8x + 6y = 48.
Thus,
(0, 0) assures the in equation 8x + 6y ≤ 48.
Thus,
The area in xy-plane that have the origin shows the solution set of the given equation.
x = 5 is the line passing through x = 5 parallel to the Y axis.
y = 6 is the line passing through y = 6 parallel to the X axis.
The area shown by x ≥ 0 and y ≥ 0:
Hence,
All the point in the first quadrant assure these in equations.
Thus,
The first quadrant is the area shows by the in equations.
These lines are drawn using a suitable scale.

The corner points of the suitable area are O(0, 0), G(5, 0), F 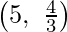 , E
, E 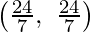
and B(0, 6).
The values of Z at these corner points are as follows.
Corner point
| Z = 4x + 3y
|
O(0, 0)
| 4× 0 + 3 × 0 = 0
|
G(5, 0)
| 4 × 5 + 3 × 0 = 20
|
F 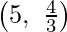
| 4 × 5 + 3 × 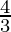 = 24 = 24
|
E 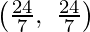
| 4 × 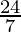 + 3 × + 3 × 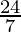 = = 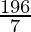 = 24 = 24
|
B(0, 6)
| 4 × 0 + 3 × 6 = 18
|
Here we can see that the maximum value of the objective function Z is 24
Which is at F 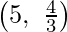 and E
and E
Therefore,
The best value of Z is 24.
Question 6. Maximize Z = 15x + 10y
Subject to
3x + 2y ≤ 80
2x + 3y ≤ 70
x, y ≥ 0
Solution:
Convert the given in equations into equations,
We will get the following equations:
3x + 2y = 80, 2x + 3y = 70, x = 0 and y = 0
The area shown by 3x + 2y ≤ 80 :
The line 3x + 2y = 80 connects the coordinate axes at A 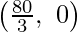 , 0 and B(0, 40) respectively.
, 0 and B(0, 40) respectively.
By connecting these points we will get the line 3x + 2y = 80.
Thus,
(0,0) assure the in equation 3x + 2y ≤ 80 .
Thus,
The area having the origin represents the solution set of the in equation 3x + 2y ≤ 80 .
The area shown by 2x + 3y ≤ 70:
The line 2x + 3y = 70 connects the coordinate axes at C(35, 0)C35, 0 and D(0, 703)D0, 703 respectively.
After connecting these points we will get the line 2x + 3y ≤ 70.
Thus,
(0,0) assure the in equation 2x + 3y ≤ 70.
Thus,
The area having the origin shows the solution set of the in equation 2x + 3y ≤ 70.
The area shown by x ≥ 0 and y ≥ 0:
Hence,
Every point in the first quadrant assure these in equations.
Thus,
The first quadrant is the area shown by the in equations x ≥ 0 and y ≥ 0.
The suitable area determined by the system of constraints, 3x + 2y ≤ 80, 2x + 3y ≤ 70, x ≥ 0, and y ≥ 0 are as follows.

The corner points of the suitable area are O(0, 0), A 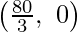 , 0 ,E(20, 10) and D
, 0 ,E(20, 10) and D 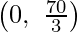 .
.
The values of Z at these corner points are as follows.
Corner point
| Z = 15x + 10y
|
O(0, 0)
| 15 × 0 + 10 × 0 = 0
|
A 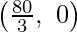
| 15 × 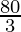 + 10 × 0 = 400 + 10 × 0 = 400
|
E(20, 10)
| 15 × 20 + 10 × 10 = 400
|
D 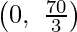
| 15 × 0 + 10 ×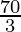 = = 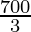
|
Thus we can see that the maximum value of the objective function Z is 400 which is at A 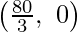 ,
,
and E(20, 10).
Therefore,
The best value of Z is 400.
Question 7. Maximize Z = 10x + 6y
Subject to
3x + y ≤ 12
2x + 5y ≤ 34
x, y ≥ 0
Solution:
Convert the given in equations into equations,
We will get the following equations:
3x + y = 12, 2x + 5y = 34, x = 0 and y = 0
The area shown by 3x + y ≤ 12:
The line 3x + y = 12 connects the coordinate axes at A(4, 0) and B(0, 12) respectively.
After connecting these points we will get the line 3x + y = 12.
Thus,
(0,0) assure the in equation 3x + y ≤ 12.
Thus,
The area having the origin represents the solution set of the in equation 3x + y ≤ 12.
The area shown by 2x + 5y ≤ 34:
The line 2x + 5y = 34 connects the coordinate axes at C(17, 0) and D 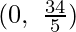 respectively.
respectively.
After connecting these points we will get the line 2x + 5y ≤ 34.
Thus,
(0,0) assure the in equation 2x + 5y ≤ 34.
Thus,
The area having the origin represents the solution set of the in equation 2x + 5y ≤ 34.
Area having by x ≥ 0 and y ≥ 0:
Hence,
All the point in the first quadrant assure these in equations.
Thus,
The first quadrant is the area shown by the in equations x ≥ 0 and y ≥ 0.
The suitable area determined by the system of constraints, 3x + y ≤ 12, 2x + 5y ≤ 34, x ≥ 0, and y ≥ 0 are as follows.

The corner points of the suitable area are O(0, 0), A(4, 0) ,E(2, 6) and D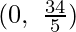 .
.
The values of Z at these corner points are as follows:
Corner point
| Z = 10x + 6y
|
O(0, 0)
| 10 × 0 + 6 × 0 = 0
|
A(4, 0)A4, 0
| 10× 4 + 6 × 0 = 40
|
E(2, 6)E2, 6
| 10 × 2 + 6 × 6 = 56
|
D 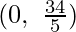
| 10 × 0 + 6 ×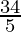 = = 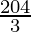
|
Here we can see that the maximum value of the objective function Z is 56 which is at E(2, 6) that means at x = 2 and y = 6.
Therefore,
The best value of Z is 56.
Question 8. Maximize Z = 3x + 4y
Subject to
2x + 2y ≤ 80
2x + 4y ≤ 120
Solution:
Here we have to maximize Z = 3x + 4y
Convert the given in equations into equations, we will get the following equations:
2x + 2y = 80, 2x + 4y = 120
The area shown by 2x + 2y ≤ 80:
The line 2x + 2y = 80 connects the coordinate axes at A(40, 0) and B(0, 40) respectively.
After connecting these points we will get the line 2x + 2y = 80.
Thus,
(0,0) assure the in equation 2x + 2y ≤ 80.
Thus,
The area having the origin represents the solution set of the in equation 2x + 2y ≤ 80.
The area shown by 2x + 4y ≤ 120:
The line 2x + 4y = 120 connects the coordinate axes at C(60, 0) and D(0, 30) respectively.
After connecting these points we will get the line 2x + 4y ≤ 120.
Thus,
(0,0) assure the in equation 2x + 4y ≤ 120.
Thus,
The area having the origin represents the solution set of the in equation 2x + 4y ≤ 120.
The suitable area determined by the system of constraints, 2x + 2y ≤ 80, 2x + 4y ≤ 120 are as follows:

The corner points of the suitable area are O(0, 0), A(40, 0), E(20, 20) and D(0, 30).
The values of Z at these corner points are as follows:
Corner point
| Z = 3x + 4y
|
O(0, 0)
| 3 × 0 + 4 × 0 = 0
|
A(40, 0)
| 3× 40 + 4 × 0 = 120
|
E(20, 20)
| 3 × 20 + 4 × 20 = 140
|
D(0, 30)
| 10 × 0 + 4 ×30 = 120
|
Here we can see that the maximum value of the objective function Z is 140 which is at E(20, 20) that means at
x = 20 and y = 20.
Therefore,
The best value of Z is 140.
Question 9. Maximize Z = 7x + 10y
Subject to
x + y ≤ 30000
y ≤ 12000
x ≥ 6000
x ≥ y
x, y ≥ 0
Solution:
Here we have to maximize Z = 7x + 10y
Convert the given in equations into equations,
We will get the following equations:
x + y = 30000,y = 12000, x = 6000, x = y, x = 0 and y = 0.
Region represented by x + y ≤ 30000:
The line x + y = 30000 connects the coordinate axes at A(30000, 0) and B(0, 30000) respectively.
After connecting these points we will get the line x + y = 30000.
Thus, (0,0) assure the in equation x + y ≤ 30000.
Thus,
the area having the origin represents the solution set of the in equation x + y ≤ 30000.
The line y = 12000 is the line that passes through C(0,12000) and parallel to x axis.
The line x = 6000 is the line that passes through (6000, 0) and parallel to y axis.
The area shown by x ≥ y
The line x = y is the line that passes through origin.The points to the right of the line x = y assure the inequation x ≥ y.
Like by taking the point (−12000, 6000).
Here, 6000 > −12000 which implies y > x.
Hence,
the points to the left of the line x = y will not assure the given inequation x ≥ y.
The area shown by x ≥ 0 and y ≥ 0:
Hence,
All the point in the first quadrant assure these inequations.
Thus,
the first quadrant is the area shown by the inequations x ≥ 0 and y ≥ 0.
The suitable area determined by the system of constraints, x + y ≤ 30000, y ≤ 12000, x ≥ 6000, x ≥ y , x ≥ 0 and y ≥ 0 are as follows:

The corner points of the feasible region are
D(6000, 0),
A(3000,
F(18000, 12000) and
E(12000, 12000).
The values of Z at these corner points are as follows:
Corner point
| Z = 7x + 10y
|
D(6000, 0)
| 7 × 6000 + 10 × 0 = 42000
|
A(3000, 0)A3000, 0
| 7× 3000 + 10 × 0 = 21000
|
F(18000, 12000)
| 7 × 18000 + 10 × 12000 = 246000
|
E(12000, 12000)
| 7 × 12000 + 10 ×12000 = 204000
|
Here we can see that the maximum value of the objective function Z is 246000 which is at F(18000, 12000) that means at
x = 18000 and y = 12000.
Therefore,
The best value of Z is 246000.
Question 10. Minimize Z = 2x + 4y
Subject to
x + y ≥ 8
x + 4y ≥ 12
x ≥ 3, y ≥ 2
Solution:
Convert the given in equations into equations, we will get the following equations:
x + y = 8, x + 4y = 12, x = 3, y = 2
The area shows by x + y ≥ 8:
The line x + y = 8 connects the coordinate axes at A(8, 0) and B(0, 8) respectively.
After connecting these points we will get the line x + y = 8.
Thus,
(0,0) does not assure the in equation x + y ≥ 8.
Thus,
The region in xy plane which does not contain the origin represents the solution set of the in equation x + y ≥ 8.
The area shown by x + 4y ≥ 12:
The line x + 4y = 12 connects the coordinate axes at C(12, 0) and D(0, 3) respectively.
After connecting these points we will get the line x + 4y = 12.
Thus,
(0,0) assure the in equation x + 4y ≥ 12.
Thus,
the area in xy plane which having the origin represents the solution set of the in equation x + 4y ≥ 12.
The line x = 3 is the line that passes through the point (3, 0) and is parallel to Y axis.x ≥ 3 is the area to the right of the line
x = 3.
The line y = 2 is the line that passes through the point (0, 12) and is parallel to X axis.y ≥ 2 is the area above the line y = 2.

The corner points of the suitable region are E(3, 5) and F(6, 2).
The values of Z at these corner points are as follows.
| Corner point | Z = 2x + 4y
|
E(3, 5)
| 2 × 3 + 4 × 5 = 26
|
F(6, 2)
| 2 × 6 + 4 × 2 = 20
|
Therefore,
The minimum value of Z is 20 at the point F(6, 2).
Hence, x = 6 and y =2 is the best solution of the given LPP.
Therefore,
The best value of Z is 20.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...