Question 27. (x2 – 2xy)dy + (x2 – 3xy + 2y2)dx = 0
Solution:
We have,
(x2 – 2xy)dy + (x2 – 3xy + 2y2)dx = 0
(dy/dx) = (x2 – 3xy + 2y2)/(2xy – y2)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = (x2 – 3xvx + 2v2x2)/(2xvx – x2)
v + x(dv/dx) = (1 – 3v + 2v2)/(2v – 1)
x(dv/dx) = [(1 – 3v + 2v2)/(2v – 1)] – v
x(dv/dx) = (1 – 3v + 2v2 – 2v2 + v)/(2v – 1)
x(dv/dx) = (1 – 2v)/(2v – 1)
x(dv/dx) = -1
dv = -(dx/x)
On integrating both sides,
∫dv = -∫(dx/x)
v = -log|x| + log|c|
(y/x) + log|x| = log|c| (Where ‘c’ is integration constant)
Question 28. x(dy/dx) = y – xcos2(y/x)
Solution:
We have,
x(dy/dx) = y – xcos2(y/x)
(dy/dx) = y/x – cos2(y/x)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = v – cos2(v)
x(dv/dx) = -cos2(v)
dv/cos2(v) = -(dx/x)
On integrating both sides,
∫dv/cos2(v) = -∫(dx/x)
∫sec2vdv = -∫(dx/x)
tan(v) = -log|x| + log|c|
tan(y/x) = log|c/x| (Where ‘c’ is integration constant)
Question 29. x(dy/dx) – y = 2√(y2 – x2)
Solution:
We have,
x(dy/dx) – y = 2√(y2 – x2)
(dy/dx) = [2√(y2 – x2) + y]/x
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
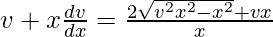
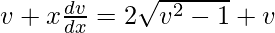
x(dv/dx) = 2√(v2 – 1)
dv/√(v2 – 1) = 2(dx/x)
On integrating both sides,
∫dv/√(v2 – 1) = 2∫(dx/x)
log|v + √(v2– 1)| = 2log(x) + log(c)
|v + √(v2 – 1)| = |cx2|
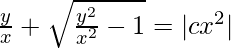
 (Where ‘c’ is integration constant)
(Where ‘c’ is integration constant)
Question 30. xcos(y/x)(ydx + xdy) = ysin(y/x)(xdy – ydx)
Solution:
We have,
xcos(y/x)(ydx + xdy) = ysin(y/x)(xdy – ydx)
xycos(y/x)dx + x2cos(y/x)dy = xysin(y/x)dy – y2sin(y/x)dx
x2cos(y/x)dy – xysin(y/x)dy = -y2sin(y/x)dx – xycos(y/x)dx
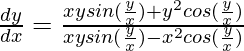
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
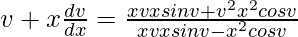
v + x(dv/dx) = (vcosv + v2sinv)/(vsinv – cosv)
x(dv/dx) = [(vcosv + v2sinv)/(vsinv – cosv)] – v
x(dv/dx) = (vcosv + v2sinv – v2sinv + vcosv)/(vsinv – cosv)
x(dv/dx) = (2vcosv)/(vsinv – cosv)
[(vsinv – cosv)/(vcosv)]dv = 2(dx/x)
On integrating both sides,
∫tanvdv – ∫(dv/v) = 2log|x| + log|c|
log|secv| – log|v| = log|cx2|
log|(secv/v)| = log|cx2|
(x/y)sec(y/x) = cx2
sec(y/x) = cxy (Where ‘c’ is integration constant)
Question 31. (x2 + 3xy + y2)dx – x2dy = 0
Solution:
We have,
(x2 + 3xy + y2)dx – x2dy = 0
dy/dx = (x2 + 3xy + y2)/x2
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = (x2 + 3xvx + v2x2)/x2
v + x(dv/dx) = (1 + 3v + v2)
x(dv/dx) = (1 + 3v + v2) – v
x(dv/dx) = (1 + 2v + v2)
x(dv/dx) = (1 + v)2
dv/(1 + v)2 = (dx/x)
On integrating both sides,
∫dv/(1 + v)2 = ∫(dx/x)
-[1/(v + 1)] = log|x| – c
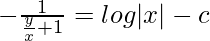
x/(x + y) + log|x| = c (Where ‘c’ is an integration constant)
Question 32. (x – y)(dy/dx) = (x + 2y)
Solution:
We have,
(x – y)(dy/dx) = (x + 2y)
(dy/dx) = (x + 2y)/(x – y)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = (x + 2vx)/(x – vx)
v + x(dv/dx) = (1 + 2v)/(1 – v)
x(dv/dx) = [(1 + 2v)/(1 – v)] – v
x(dv/dx) = (1 + 2v – v + v2)/(1 – v)
x(dv/dx) = (1 + v + v2)/(1 – v)
(1 – v)dv/(1 + v + v2) = (dx/x)
On integrating both sides,
∫[(1 – v)/(1 + v + v2)]dv = ∫(dx/x)
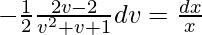
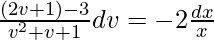
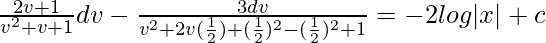
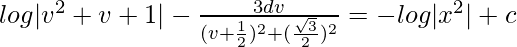
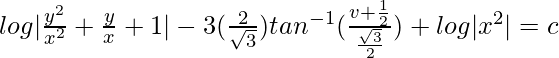
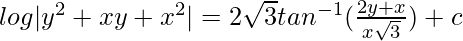 (Where ‘c’ is an integration constant)
(Where ‘c’ is an integration constant)
Question 33. (2x2y + y3)dx + (xy2 – 3x2)dy = 0
Solution:
We have,
(2x2y + y3)dx + (xy2 – 3x2)dy = 0
dy/dx = (2x2y + y3)/(3x3 – xy2)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = (2x2vx + v3x3)/(3x3 – xv2x2)
v + x(dv/dx) = (2v + v3)/(3 – v3)
x(dv/dx) = [(2v + v3)/(3 – v3)] – v
x(dv/dx) = (2v + v3 – 3v + v3)/(3 – v3)
(3 – v3)dv/(2v3 – v) = (dx/x)
On integrating both sides,
∫[(3 – v3)/(2v3 – v)]dv = ∫(dx/x)
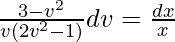
Using partial fraction,
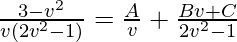
3 – v2 = A(2v2 – 1) + (Bv + C)v
3 – v2 = 2Av2 – A + Bv2 + Cv
3 – v2 = v2(2A + B) + Cv – A
On comparing the coefficients, we get
A = -3,
B = 5,
C = 0,
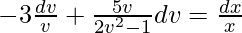
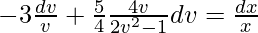
-3log|v|+(5/4)log|2v2-1|=log|x|+log|c|
-12log|v|+5log|2v2-1|=4log|x|+4log|c|
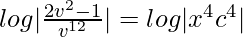
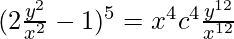
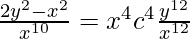
|2y2 – x2|5 = x2c4y12 (Where ‘c’ is an integration constant)
Question 34. x(dy/dx) – y + xsin(y/x) = 0
Solution:
We have,
x(dy/dx) – y + xsin(y/x) = 0
x(dy/dx) = y – xsin(y/x)
(dy/dx) = [y – xsin(y/x)]/x
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = [vx – xsinv]/x
v + x(dv/dx) = (v – sinv)
x(dv/dx) = -sinv
cosecvdv = -(dx/x)
On integrating both sides,
∫cosecvdv = -∫(dx/x)
-log|cosecv + cotv| = -log|x| + log|c|
-log|(1/sinv) + (cosv/sinv)| = -log|x/c|
|(1 + cosv)/sinv| = |x/c|
xsinv = c(1 + cosv)
xsin(y/x) = c[1 + cos(y/x)] (Where ‘c’ is integration constant)
Question 35. ydx + {xlog(y/x)}dy – 2xydy = 0
Solution:
We have,
ydx + {xlog(y/x)}dy – 2xydy = 0
y + {xlog(y/x)}(dy/dx) – 2xy = 0
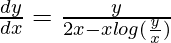
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
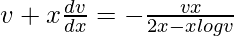
v + x(dv/dx) = v/(2 – logv)
x(dv/dx) = [v/(2 – logv)] – v
x(dv/dx) = (v – 2v + vlogv)/(2 – logv)
x(dv/dx) = -v(logv – 1)/(logv – 2)
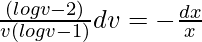
On integrating both sides,
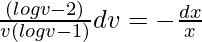
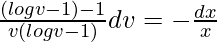
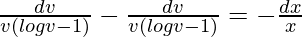
Let. logv – 1 = z
On differentiating both sides,
(dv/v) = dz
∫dz – ∫(dz/z) = -∫(dx/x)
z – log|z| = -log|x| + log|c|
(logv – 1) – log|(logv – 1)| = -log|x| + log|c|
logv – log|logv – 1| = -log|x| + log|c| + 1
log|(logv – 1)/v| = log|c1x|
|logv – 1| = |c1xv|
|log(y/x) – 1| = |c1x(y/x)|
|log(y/x) – 1| = |c1y| (Where ‘c1’ is integration constant)
Question 36(i). (x2 + y2)dx = 2xydy, y(1) = 0
Solution:
We have,
(x2 + y2)dx = 2xydy
(dy/dx) = (x2 + y2)/2xy
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = (x2 + v2x2)/2vx2
v + x(dv/dx) = (1 + v2)/2v
x(dv/dx) = [(1 + v2)/2v] – v
x(dv/dx) = (1 + v2 – 2v2)/2v
x(dv/dx) = (1 – v2)/2v
2vdv/(1 – v2) = (dx/x)
On integrating both sides,
∫2vdv/(1 – v2) = ∫(dx/x)
-log|1 – v2| = log|x| – log|c|
log|1 – v2| = log|c/x|
|1 – y2/x2| = |c/x|
|x2 – y2| = |cx|
At x = 1, y = 0
1 – 0 = c
c = 1
|x2 – y2| = |x|
(x2 – y2) = x
Question 36(ii). xex/y – y + x(dy/dx) = 0, y(e) = 0
Solution:
We have,
xex/y – y + x(dy/dx) = 0
(dy/dx) = (y – xex/y)/x
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = (vx – xev)/x
v + x(dv/dx) = v – ev
x(dv/dx) = v – ev – v
x(dv/dx) = -ev
e-vdv = -(dx/x)
On integrating both sides,
∫e-vdv = -∫(dx/x)
-e-v = -log|x| – log|c|
e-v = log|x| + log|c|
e-(y/x) = log|x| + log|c|
At x = e, y = 0
e-(0/e) = log|e| + log|c|
1 = 1 + log|c|
c = 0
e-y/x = logx
Question 36(iii). (dy/dx) – (y/x) + cosec(y/x) = 0, y(1) = 0
Solution:
We have,
(dy/dx) – (y/x) + cosec(y/x) = 0
(dy/dx) = (y/x) – cosec(y/x)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = v – cosec(v)
x(dv/dx) = v – cosec(v) – v
x(dv/dx) = -cosec(v)
-sin(v)dv = (dx/x)
On integrating both sides,
-∫sin(v)dv = ∫(dx/x)
cos(v) = log|x| + log|c|
cos(y/x) = log|x| + log|c|
At x = 1, y = 0
cos(0/1) = log|1| + log|c|
1 = 0 + log|c|
log|c| = 1
cos(y/x) = log|x| + 1
log|x| = cos(y/x) – 1
Question 36(iv). (xy – y2)dx – x2dy = 0, y(1) = 1
Solution:
We have,
(xy – y2)dx – x2dy = 0
(dy/dx) = (xy – y2)/x2
(dy/dx) = (y/x) – (y2/x2)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = v – v2
x(dv/dx) = v – v2 – v
x(dv/dx) = -v2
-(dv/v2) = (dx/x)
On integrating both sides,
-∫(dv/v2) = ∫(dx/x)
-(-1/v) = log|x| + c
(1/v) = log|x| + c
x/y = log|x| + c
At x = 1, y = 1
1 = log|1| + c
c = 1
x/y = log|x| + 1
y = x/[log|x| + 1]
Question 36(v). (dy/dx) = [y(x + 2y)]/[x(2x + y)]
Solution:
We have,
(dy/dx) = [y(x + 2y)]/[x(2x + y)]
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = [vx(x + 2vx)]/[x(2x + vx]
x(dv/dx) = [vx(x + 2vx)]/[x(2x + vx] – v
x(dv/dx) = (v + 2v2 – 2v – v2)/(2 + v)
x(dv/dx) = (v2 – v)/(2 + v)
(2 + v)dv/[v(v – 1)] = (dx/x)
On integrating both sides,
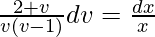
Using partial derivative,
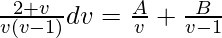
2 + v = A(v – 1) + B(v)
2 + v = v(A + B) – A
On comparing the coefficients,
A = -2
B = 3
-2∫(dv/v) + 3∫dv/(v – 1) = ∫(dx/x)
-2log|v| + 3log|v – 1| = log|x| + log|c|
log|(v – 1)3/v2| = log|xc|
(v – 1)3 = v2|xc|
(y – x)3/x3 = (y/x)2|xc|
(y – x)3 = y2x2c
At x = 1, y = 2,
(2 – 1)3 = 4 * 1 * c
c = (1/4)
(y – x)3 = (1/4)y2x2
Question 36(vi). (y4 – 2x3y)dx + (x4 – 2xy3)dy = 0, y(1) = 0
Solution:
We have,
(y4 – 2x3y)dx + (x4 – 2xy3)dy = 0
dy/dx = (2x3y – y4)/(x4 – 2xy3)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = (2x3vx – v4x4)/(x4 – 2xv3x3)
v + x(dv/dx) = (2v – v4)/(1 – 2v3)
x(dv/dx) = [(2v – v4)/(1 – 2v3)] – v
x(dv/dx) = (2v – v4 – v + 2v4)/(1 – 2v3)
x(dv/dx) = (v + v4)/(1 – 2v3)
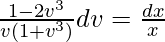
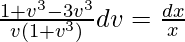
On integrating both sides,
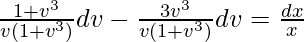
∫(dv/v) – ∫(3v2)dv/(1 + v3) = log|x| + log|c|
log|v| – log|1 + v3| = log|xc|
log|v/(1 + v3)| = log|xc|
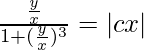
At x = 1, y = 1,
1/(1 + 1) = c
c = (1/2)
(yx2)/(x3 + y3) = (1/2)x
Question 36(vii). x(x2 + 3y2)dx + y(y2 + 3x2)dy = 0, y(1) = 1
Solution:
We have,
x(x2 + 3y2)dx + y(y2 + 3x2)dy = 0
dy/dx = -[x(x2 + 3y2)/y(y2 + 3x2)]
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
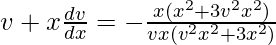
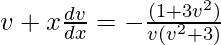
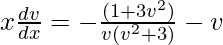
x(dv/dx) = -(1 + 3v2 + v4 + 3v2)/v(v2 + 3)
[(v3 + 3v)/(1 + 6v2 + v4)]dv = -(dx/x)
Multiply both sides with 4 and integrating,
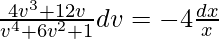
log|v4 + 6v2 + 1| = -log|x|4 + log|c|
|v4 + 6v2 + 1| = |c/x4|
(y4 + 6x2y2 + x4) = c
At y = 1, x = 1
(1 + 6 + 1) = c
c = 8
(y4 + 6x2y2 + x4) = 8
Question 36(viii). {xsin2(y/x) – y}dx + xdy = 0, y(1) = π/4
Solution:
We have,
{xsin2(y/x) – y}dx + xdy = 0
dy/dx = [y – xsin2(y/x)]/x
dy/dx = (y/x) – sin2(y/x)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = v – sin2(v)
x(dv/dx) = v – sin2(v) – v
x(dv/dx) = -sin2(v)
-cosec2(v)dv = (dx/x)
On integrating both sides,
-∫cosec2(v) = ∫(dx/x)
cot(v) = log|x| + log|c|
cot(y/x) = log|xc|
At x = 1, y = π/4
cot(π/4) = log|c|
log|c| = 1
c = e
cot(y/x) = log|ex|
Question 36(ix). x(dy/dx) – y + xsin(y/x) = 0, y(2) = π
Solution:
We have,
x(dy/dx) – y + xsin(y/x) = 0
x(dy/dx) = y – xsin(y/x)
(dy/dx) = (y/x) – sin(y/x)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = v – sin(v)
x(dv/dx) = v – sin(v) – v
x(dv/dx) = -sin(v)
-cosec(v)dv = (dx/x)
On integrating both sides,
∫cosec(v) = -∫(dx/x)
log|cosec(v) – cot(v)| = -log|x| + log|c|
log|cosec(v) – cot(v)| = -log|x| + log|c|
log|cosec(y/x) – cot(y/x)| = -log|x| + log|c|
At x = 2, y = π
|cosec(π/2) – cot(π/2)| = -log|2| + log|c|
log|c| = 0
log|cosec(y/x) – cot(y/x)| = -log|x|
Question 37. xcos(y/x)(dy/dx) = ycos(y/x) + x, When x = 1, y = π/4
Solution:
We have,
xcos(y/x)(dy/dx) = ycos(y/x) + x
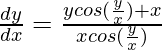
(dy/dx) = (y/x) + [1/cos(y/x)]
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = v + 1/cosv
x(dv/dx) = v + 1/cosv – v
x(dv/dx) = 1/cosv
cosvdv = (dx/x)
On integrating both sides,
∫cosvdv = ∫(dx/x)
sin(v) = log|x| + log|c|
sin(y/x) = log|x| + log|c|
At x = 1, y = π/4
1/√2 = 0 + log|c|
log|c| = (1/√2)
sin(y/x) = log|x| + (1/√2)
Question 38. (x – y)(dy/dx) = (x + 2y), when x = 1,y = 0
Solution:
We have,
(x – y)(dy/dx) = (x + 2y)
(dy/dx) = (x + 2y)/(x – y)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = (x + 2vx)/(x – vx)
v + x(dv/dx) = (1 + 2v)/(1 – v)
x(dv/dx) = [(1 + 2v)/(1 – v)] – v
x(dv/dx) = (1 + 2v – v + v2)/(1 – v)
(1 – v)dv/(1 + v + v2) = (dx/x)
On integrating both sides,
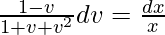
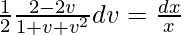
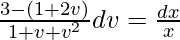
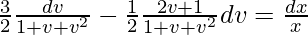
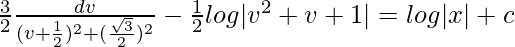
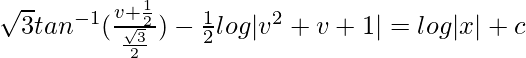
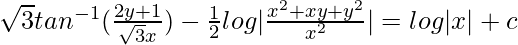
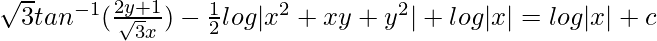
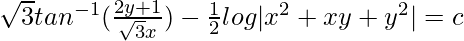
At x = 1, y = 0
√3tan-1|1/√3| – (1/2)log|1| = c
c = √3(π/6)
c = (π/2√3)
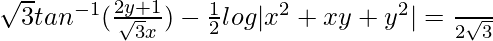
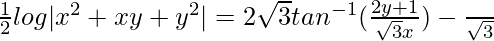
Question 39. (dy/dx) = xy/(x2 + y2)
Solution:
We have,
(dy/dx) = xy/(x2 + y2)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = xvx/(x2 + v2x2)
v + x(dv/dx) = v/(1 + v2)
x(dv/dx) = [v/(1 + v2)] – v
x(dv/dx) = (v – v – v3)/(1 + v2)
[-(1/v3) – (1/v)]dv = (dx/x)
On integrating both sides,
-∫dv/v3 – ∫dv/v = ∫(dx/x)
(1/2v2) – log|v| = log|x| + c
(x2/2y2) = log|vx| + c
(x2/2y2) = log|(y/x)x| + c
(x2/2y2) = log|y| + c
At x = 0, y = 1
c = 0
(x2/2y2) = log|y|
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...