Class 12 RD Sharma Solutions – Chapter 14 Differentials, Errors and Approximations – Exercise 14.1 | Set 1
Last Updated :
12 Dec, 2021
Question 1: If y=sin x and x changes from π/2 to 22/14, what is the approximate change in y?
Solution:
According to the given condition,
x = π/2, and
x+△x = 22/14
△x = 22/14-x = 22/14 – π/2
As, y = sin x
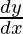 = cos x
= cos x
 = cos (π/2) = 0
= cos (π/2) = 0
△y =  △x
△x
△y = 0 △x
△y = 0 (22/14 – π/2)
△y = 0
Hence, there will be no change in y.
Question 2: The radius of a sphere shrinks from 10 to 9.8 cm. Find approximately the decrease in its volume?
Solution:
According to the given condition,
Let’s take radius as x
x = 10, and
Let △x be the error in the radius and △y be the error in the volume
x+△x = 9.8
△x = 9.8-x = 9.8-10 = -0.2
As, Volume of sphere = 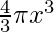
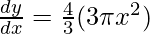 = 4πx2
= 4πx2
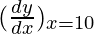 = 4π(10)2 = 400 π
= 4π(10)2 = 400 π
△y = 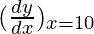 △x
△x
△y = (400 π) (-0.2)
△y = -80 π
Hence, approximate decrease in its volume will be -80 π cm3
Question 3: The circular metal plate expands under heating so that its radius increases by k%. Find the approximate increase in the area of the plate, if the radius of the plate before heating is 10 cm.
Solution:
According to the given condition,
Let’s take radius as x
x = 10, and
Let △x be the error in the radius and △y be the error in the surface area
△x/x × 100 = k
△x = (k × 10)/100 = k/10
As, Area of circular metal = πx2
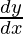 = π(2x) = 2πx
= π(2x) = 2πx
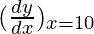 = 2π(10) = 20 π
= 2π(10) = 20 π
△y = 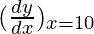 △x
△x
△y = (20 π) (k/10)
△y = 2kπ
Hence, approximate increase in the area of the plate is 2kπ cm2
Question 4: Find the percentage error in calculating the surface area of a cubical box if an error of 1% is made in measuring the lengths of edges of the cube.
Solution:
According to the given condition,
Let △x be the error in the length and △y be the error in the surface area
Let’s take length as x
△x/x × 100 = 1
△x = x/100
x+△x = x+(x/100)
As, surface area of the cube = 6x2
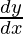 = 6(2x) = 12x
= 6(2x) = 12x
△y = 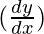 △x
△x
△y = (12x) (x/100)
△y = 0.12 x2
So, △y/y = 0.12 x2/6 x2 = 0.02
Percentage change in y = △y/y × 100 = 0.02 × 100 = 2
Hence, the percentage error in calculating the surface area of a cubical box is 2%
Question 5: If there is an error of 0.1% in the measurement of the radius of a sphere, find approximately the percentage error in the calculation of the volume of the sphere.
Solution:
According to the given condition,
As, Volume of sphere = 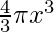
Let △x be the error in the radius and △y be the error in the volume
△x/x × 100 = 0.1
△x/x = 1/1000
As, y = 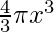
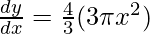 = 4πx2
= 4πx2
dy = 4πx2 dx
△y = (4πx2) △x
Change in volume,
△y/y = 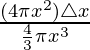
△y/y = 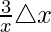
△y/y = 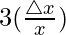 = 3(0.001) = 0.003
= 3(0.001) = 0.003
Percentage change in y = △y/y × 100 = 0.003 × 100 = 0.3
Hence, approximately the percentage error in the calculation of the volume of the sphere is 0.3%
Question 6: The pressure p and the volume v of a gas are connected by the relation pv1.4 = constant. Find the percentage error in p corresponding to a decrease of 1/2% in v.
Solution:
According to the given condition,
 = – 1/2%
= – 1/2%
pv1.4 = constant = k(say)
Taking log on both sides, we get
log(pv1.4) = log (k)
log(p)+log(v1.4) = log k
log(p) + 1.4 log(v) = log k
Differentiating wrt v, we get
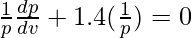
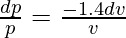
Percentage change in p = △p/p × 100 = 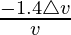 × 100 = -1.4
× 100 = -1.4 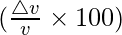
= -1.4 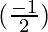
= 0.7 %
Hence, percentage error in p is 0.7%.
Question 7: The height of a cone increases by k%, its semi-vertical angle remaining the same. What is the approximate percentage increase?
Solution:
According to the given condition,
Let h be the height, y be the surface area. V be the volume, l be the slant height and r be the radius of the cone.
Let △h be the change in the height. △r be the change in the radius of base and △l be the change in slant height.
Semi-vertical angle remaining the same.
△h/h = △r/r = △l/l
and,
△h/h × 100 = k
△h/h × 100 = △r/r × 100 = △l/l × 100 = k
(i) in total surface area, and
Solution:
Total surface area of the cone
y = πrl + πr2
Differentiating both the sides wrt r, we get
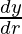 = πl + πr
= πl + πr 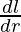 + 2πr
+ 2πr
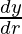 = πl + πr
= πl + πr 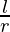 + 2πr
+ 2πr
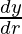 = πl + πl + 2πr
= πl + πl + 2πr
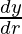 = 2πl + 2πr = 2π(r+l)
= 2πl + 2πr = 2π(r+l)
△y = 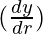 △r
△r
△y = (2π(r+l)) 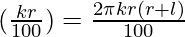
Percentage change in y = △y/y × 100 = 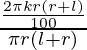 × 100
× 100
= 2k %
Hence, percentage increase in total surface area of cone 2k%.
(ii) in the volume assuming that k is small?
Solution:
Volume of cone (y) = 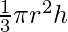
Differentiating both the sides wrt h, we get
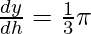 (r2 + h(2r
(r2 + h(2r 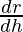 )
)
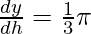 (r2 + h(2r
(r2 + h(2r 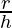 )
)
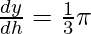 (r2 + 2r2)
(r2 + 2r2)
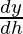 = πr2
= πr2
△y = 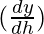 △h
△h
△y = (πr2) 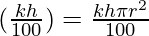
Percentage change in y = △y/y × 100 = 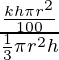 × 100
× 100
= 3k %
Hence, percentage increase in the volume of cone 3k%.
Question 8: Show that the relative error in computing the volume of a sphere, due to an error in measuring the radius, is approximately equal to the three times the relative error in the radius.
Solution:
According to the given condition,
Let △x be the error in the radius and △y be the error in volume.
Volume of cone (y) = 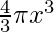
Differentiating both the sides wrt x, we get
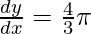 (3x2)
(3x2)
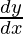 = 4πx2
= 4πx2
△y = 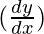 △x
△x
△y = (4πx2) (△x)
△y/y = 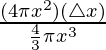
△y/y = 
Hence proved!!
Question 9: Using differentials, find the approximate values of the following:
(i) 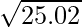
Solution:
Considering the function as
y = f(x) = 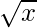
Taking x = 25, and
x+△x = 25.02
△x = 25.02-25 = 0.2
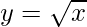

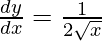
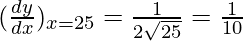
△y = dy = 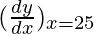 dx
dx
△y = 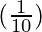 △x
△x
△y = 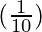 (0.02) = 0.002
(0.02) = 0.002
Hence, 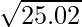 = y+△y = 5 + 0.002 = 5.002
= y+△y = 5 + 0.002 = 5.002
(ii) 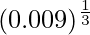
Solution:
Considering the function as
y = f(x) = 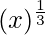
Taking x = 0.008, and
x+△x = 0.009
△x = 0.009-0.008 = 0.001
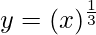
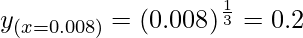

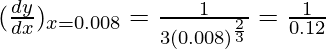
△y = dy = 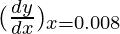 dx
dx
△y = 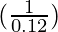 △x
△x
△y = 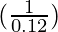 (0.001) =
(0.001) = 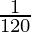 = 0.008333
= 0.008333
Hence, 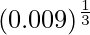 = y+△y = 0.2 + 0.008333 = 0.208333
= y+△y = 0.2 + 0.008333 = 0.208333
(iii) 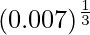
Solution:
Considering the function as
y = f(x) = 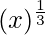
Taking x = 0.008, and
x+△x = 0.007
△x = 0.007-0.008 = -0.001
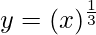
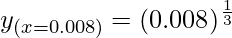 = 0.2
= 0.2

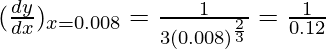
△y = dy = 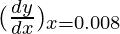 dx
dx
△y = 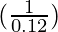 △x
△x
△y = 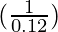 (-0.001) =
(-0.001) = 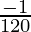 = -0.008333
= -0.008333
Hence, 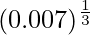 = y+△y = 0.2 + (-0.008333) = 0.191667
= y+△y = 0.2 + (-0.008333) = 0.191667
(iv) 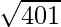
Solution:
Considering the function as
y = f(x) = 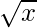
Taking x = 400, and
x+△x = 401
△x = 401-400 = 1
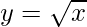
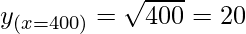
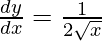
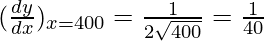
△y = dy = 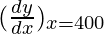 dx
dx
△y = 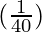 △x
△x
△y = 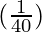 (1) = 0.025
(1) = 0.025
Hence, 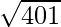 = y+△y = 20 + 0.025 = 20.025
= y+△y = 20 + 0.025 = 20.025
(v) 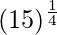
Solution:
Considering the function as
y = f(x) = 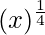
Taking x = 16, and
x+△x = 15
△x = 15-16 = -1
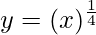
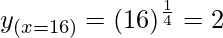
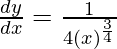
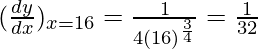
△y = dy = 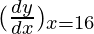 dx
dx
△y = 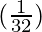 △x
△x
△y = 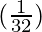 (-1) =
(-1) = 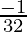 = -0.03125
= -0.03125
Hence, 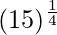 = y+△y = 0.2 + (-0.03125) = 1.96875
= y+△y = 0.2 + (-0.03125) = 1.96875
(vi) 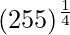
Solution:
Considering the function as
y = f(x) = 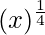
Taking x = 256, and
x+△x = 255
△x = 255-256 = -1
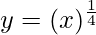
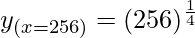 = 4
= 4
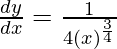
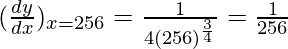
△y = dy =  dx
dx
△y = 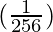 △x
△x
△y = 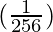 (-1) =
(-1) =  = -0.003906
= -0.003906
Hence, 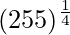 = y+△y = 0.2 + (-0.003906) = 3.9961
= y+△y = 0.2 + (-0.003906) = 3.9961
(vii) 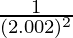
Solution:
Considering the function as
y = f(x) = 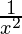
Taking x = 2, and
x+△x = 2.002
△x = 2.002-2 = 0.002
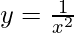
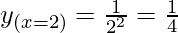
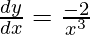
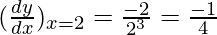
△y = dy = 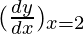 dx
dx
△y = 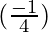 △x
△x
△y = 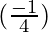 (0.002) = -0.0005
(0.002) = -0.0005
Hence, 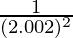 = y+△y =
= y+△y = 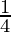 + (-0.005) = 0.2495
+ (-0.005) = 0.2495
(viii) loge 4.04, it being given that log10 4=0.6021 and log10 e=0.4343
Solution:
Considering the function as
y = f(x) = loge x
Taking x = 4, and
x+△x = 4.04
△x = 4-4.04 = 0.04
y = loge x
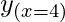 = loge 4 =
= loge 4 =  = 1.386368
= 1.386368
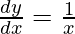

△y = dy = 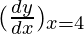 dx
dx
△y = 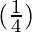 △x
△x
△y = 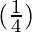 (0.04) = 0.01
(0.04) = 0.01
Hence, loge 4.04 = y+△y = 1.386368 + 0.01 = 1.396368
(ix) loge 10.02, it being given that loge 10=2.3026
Solution:
Considering the function as
y = f(x) = loge x
Taking x = 10, and
x+△x = 10.02
△x = 10.02-10 = 0.02
y = loge x
 = loge 10 = 2.3026
= loge 10 = 2.3026
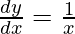
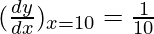
△y = dy = 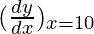 dx
dx
△y = 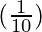 △x
△x
△y = 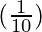 (0.02) = 0.002
(0.02) = 0.002
Hence, loge 10.02 = y+△y = 2.3026 + 0.002 = 2.3046
(x) log10 10.1, it being given that log10 e=0.4343
Solution:
Considering the function as
y = f(x) = log10 x
Taking x = 10, and
x+△x = 10.1
△x = 10.1-10 = 0.1
y = log10 x = 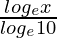
 = log10 10 = 1
= log10 10 = 1
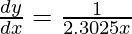
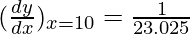
△y = dy = 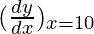 dx
dx
△y = 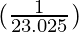 △x
△x
△y = 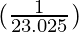 (0.1) = 0.004343
(0.1) = 0.004343
Hence, loge 10.1 = y+△y = 1 + 0.004343 = 1.004343
(xi) cos 61°, it being given that sin 60°=0.86603 and 1°=0.01745 radian.
Solution:
Considering the function as
y = f(x) = cos x
Taking x = 60°, and
x+△x = 61°
△x = 61°-60° = 1° = 0.01745 radian
y = cos x
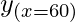 = cos 60° = 0.5
= cos 60° = 0.5
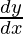 = – sin x
= – sin x
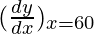 = – sin 60° = -0.86603
= – sin 60° = -0.86603
△y = dy = 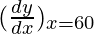 dx
dx
△y = (-0.86603) △x
△y = (-0.86603) (0.01745) = -0.01511
Hence, cos 61° = y+△y = 0.5 + (-0.01511) = 0.48489
(xii) 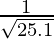
Solution:
Considering the function as
y = f(x) = 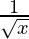
Taking x = 25, and
x+△x = 25.1
△x = 25.1-25 = 0.1

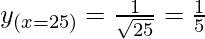
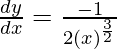
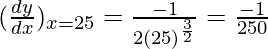
△y = dy = 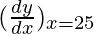 dx
dx
△y = 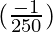 △x
△x
△y = 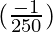 (0.1) =
(0.1) = 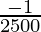 = -0.0004
= -0.0004
Hence, 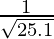 = y+△y =
= y+△y = 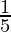 + (-0.0004) = 0.1996
+ (-0.0004) = 0.1996
(xiii) 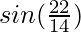
Solution:
Considering the function as
y = f(x) = sin x
Taking x = 22/7, and
x+△x = 22/14
△x = 22/14-22/7 = -22/14
sin (-22/14) = -1
y = sin x
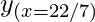 = sin (22/7) = 0
= sin (22/7) = 0
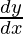 = cos x
= cos x
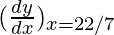 = cos (22/7)= -1
= cos (22/7)= -1
△y = dy = 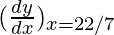 dx
dx
△y = (-1) △x
△y = (-1) (-1) = 1
Hence, sin(22/14) = 0+1 = 1
Share your thoughts in the comments
Please Login to comment...