Class 12 RD Sharma Solutions – Chapter 22 Differential Equations – Exercise 22.3 | Set 2
Last Updated :
03 Mar, 2021
Question 11: Show that y=(c-x)/(1+cx) is the solution of the differential equation.
(1+x2)(dy/dx)+(1+y2)=0
Solution:
We have,
y=(c-x)/(1+cx) (i)
Differentiating equation (i) w.r.t x,
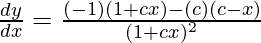
dy/dx=(-1-cx+cx-c2)/(1+cx)2
dy/dx=-(c2+1)/(1+cx2)2
L.H.S,
(1+x2)(dy/dx)+(1+y2)
=(1+x2)[-(c2+1)/(1+cx2)2]+[1+(c-x)2/(1+cx)2]
=![Rendered by QuickLaTeX.com -\frac{(1+c^2)(1+x^2)}{(1+cx)^2}+[\frac{(1+cx)^2+(c-x)^2}{(1+cx)^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aeb802acfa24e8c5985060b03304fa94_l3.png)
Simplify the above equation,
=0/(1+cx)2
=0
So, (1+x2)(dy/dx)+(1+y2)=0
Question 12: Show that y=ex(Acosx+Bsinx) is the solution of the differential equation.
d2y/dx2-2(dy/dx)+2y= 0
Solution:
we have,
y=ex(Acosx+Bsinx) (i)
Differentiating equation (i) w.r.t x,
dy/dx=ex(Acosx+Bsinx)+ex(-Asinx+Bcosx) (ii)
dy/dx=ex[(A+B)cosx-(A-B)sinx] (iii)
Again differentiating equation (ii) w.r.t x,
d2y/dx2 =ex(Acosx+Bsinx)+ex(-Asinx+Bcosx)+ex(-Asinx+Bcosx)+ex(-Acosx-Bsinx)
d2y/dx2=2ex[Bcosx-Asinx] (iv)
d2y/dx2=2ex[(A+B)cosx-(A-B)sinx] -2ex(Acosx+Bsinx)
d2y/dx2=2(dy/dx)-2y
d2y/dx2-2(dy/dx)+2y= 0
Question 13: Verify that y=cx+2c2 is a solution of the differential equation.
2(dy/dx)2+x(dy/dx)-y=0
Solution:
we have,
y=cx+2c2 (i)
Differentiating equation (i) w.r.t x,
dy/dx=c (ii)
L.H.S,
2(dy/dx)2+x(dy/dx)-y=2(c)2 +x(c)-cx+2c2
=0
Question 14: Verify that y=-x-1 is a solution of the differential equation.
(y-x)dy-(y2-x2)dx=0
Solution:
we have,
y=-x-1 (i)
Differentiating equation (i) w.r.t x,
dy/dx=-1
L.H.S,
=(y-x)dy-(y2-x2)dx
=(y-x)(dy/dx)-(y2-x2)
=(-x-1-x)(-1)-[(-x-1)2-x2]
=(2x+1)-(x2+2x+1-x2)
=(x2-x2+2x-2x-1+1)
=0
Question 15: Verify that y2=4a(x+a) is a solution of the differential equation.
y[1-(dy/dx)2]=2x(dy/dx)
Solution:
we have,
y2=4a(x+a) (i)
Differentiating equation (i) w.r.t x,
2y(dy/dx)=4a
(dy/dx)=(2a/y)
L.H.S,
=y[1-(dy/dx)2]
=y[1-(2a/y)2]
=y[1-(4a2/y2)]
=y[(y2-4a2)/y2]
=(4a(x+a)-4a2)/y
=(4ax+4a2-4a2)/y
=[2x(2a)]/y
=2x(dy/dx)
=R.H.S
Question 16: Verify that y=cetan-1 x is a solution of the differential equation.
(1+x2)(d2y/dx2)+(2x-1)(dy/dx)=0
Solution:
we have,
y=cetan-1 x (i)
Differentiating equation (i) w.r.t x,
dy/dx=cetan-1 x *(1/1+x2)
(1+x2)(dy/dx)=y (ii)
Again differentiating equation (ii) w.r.t x,
2x(dy/dx)+(1+x2)d2y/dx2=dy/dx
(2x-1)(dy/dx)+(1+x2)d2y/dx2=0
Question 17: Verify that y=em cos-1 x is a solution of the differential equation.
(1-x2)(d2y/dx2)-x(dy/dx)-m2y=0
Solution:
we have,
y=em cos-1 x (i)
Differentiating equation (i) w.r.t x,
dy/dx=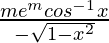
dy/dx=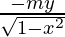 (ii)
(ii)
Again differentiating equation (ii) w.r.t x,
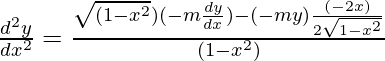
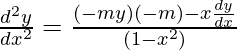
(1-x2)d2y/dx2=m2y-xdy/dx
(1-x2)d2y/dx2-m2y-xdy/dx=0
Question 18: Verify that y=log(x+1/√(x2+a2))2 is a solution of the differential equation.
(a2+x2)d2y/dx2+x(dy/dx)=0
Solution:
we have,
y=log(x+1/√(x2+a2))2 (i)
Differentiating equation (i) w.r.t x,
dy/dx=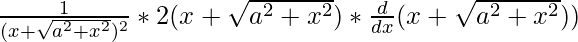
dy/dx=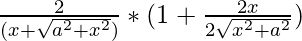
dy/dx=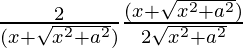
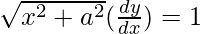 (ii)
(ii)
Again differentiating equation (ii) w.r.t x,
(√x2+a2)d2y/dx2+(1/(2√x2+a2))*(2x)*(dy/dx)=0
(a2+x2)d2y/dx2+x(dy/dx)=0
Question 19: Show that the differential equation of which y=2(x2-1)+ce-x2 is the solution
dy/dx+2xy=4x3
Solution:
we have,
y=2(x2-1)+ce-x2 (i)
Differentiating equation (i) w.r.t x,
dy/dx=4x+ce-x2(-2x)
dy/dx=4x-2cxe-x2 (ii)
L.H.S,
=dy/dx+2xy
=4x-2cxe-x2 -2x(y=2(x2-1)+ce-x2
=4x-2cxe-x2+4x3-4x+2xce-x2
=0
Question 20: Show that y=e-x+ax+c is the solution of the differential equation.
exd2y/dx2=1
Solution:
We have,
y=e-x+ax+c (i)
Differentiating equation (i) w.r.t x,
dy/dx=-e-x+a (ii)
Again differentiating equation (ii) w.r.t x,
d2y/dx2=e-1
(1/e-1)d2y/dx2=1
exd2y/dx2=1
Question 21: For each of the following differential equations verify that the accompanying function is a solution in the mentioned domain.
(i) Function, y=ax, Differential equation, x(dy/dx)=y
Solution:
We have,
y=ax (i)
Differentiating equation (i) w.r.t x,
dy/dx=a (ii)
From equation (i) a=(y/x)
Putting the value of a in equation (i)
(dy/dx)=a
(dy/dx)=(y/x)
x(dy/dx)=y
(ii) Function, y=±√(a2-x2), Differential equation: x+y(dy/dx)=0
Solution:
we have,
y=±√(a2-x2) (i)
Squaring both sides, we have
y2=(a2-x2)
2y(dy/dx)=-2x
x+y(dy/dx)=0
(iii) Function, y=a/(x+a), Differential equation, y+x(dy/dx)=y2
Solution:
We have,
y=a/(x+a) (i)
Differentiating equation (i) w.r.t x,
dy/dx=a(-1)/(x+a)2
dy/dx=-a/(x+a)2
L.H.S,
=y+x(dy/dx)
=a/(x+a)-ax/(x+a)2
=(-ax+ax+a2)/(x+a)2
=a2/(x+a)2
y2
(iv) Function, y=ax+b+1/2x, Differential equation, x3d2y/dx2=1
Solution:
We have,
y=ax+b+1/2x (i)
Differentiating equation (i) w.r.t x,
dy/dx=a+1/(-2x2)
dy/dx=a-1/2x2 (ii)
Again differentiating equation (ii) w.r.t x,
d2y/dx2=0-(-2)/(2x3)
d2y/dx2=1/x3
x3d2y/dx2=1
(v) Function, y=(1/4)*(x±a)2, Differential equation, y=(dy/dx)2
Solution:
We have,
y=(1/4)*(x±a)2
Differentiating equation (i) w.r.t x,
dy/dx=(1/4)*2(x±a)
Squaring both side, we have
(dy/dx)2=(1/4)*(x±a)2
(dy/dx)2=y
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...