Class 12 RD Sharma Solutions – Chapter 22 Differential Equations – Exercise 22.11 | Set 3
Last Updated :
24 Jan, 2023
Question 23. At every point on a curve, the slope is the sum of the abscissa and the product of the ordinate and the abscissa, and the curve passes through (0, 1) Find the equation of the curve.
Solution:
Slope is given by, (dy/dx)
We have,
(dy/dx) = x + xy
(dy/dx) = x(y + 1)
dy/(y + 1) = xdx
On integrating both sides, we get
∫dy/(y + 1) = ∫xdx
Log|y + 1| = (x2/2) + c …(i)
Since the curve is passing through (0, 1)
Log|2| = c
Log|y + 1| = (x2/2) + Log|2|
Log|(y + 1)/2| = x2/2
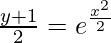
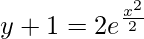
Question 24. A curve is such that the length of the perpendicular from the origin on the tangent any point of the curve is equal to the abscissa of P. Prove that the differential equation of the curve is y2 – 2xy(dy/dx) – x2 = 0, and hence find the curve.
Solution:
Tangent of the curve is given by,
Y – y = (dy/dx)(X – x)
If P be perpendicular from the origin, then
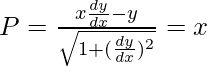
x2(dy/dx)2 – 2xy(dy/dx) + y2 = x2 + x2(dy/dx)2
y2 – 2xy(dy/dx) – x2 = 0
Hence Proved.
Now we find the curve
So, we have y2 – 2xy(dy/dx) – x2 = 0
(dy/dx) = (y2 – x2)/2xy
Above equation is homogeneous equation.
Let, y = vx
On differentiating both sides we have,
(dy/dx) = v + x(dv/dx)
v + x(dv/dx) = (v2x2 – x2)/2xvx
v + x(dv/dx) = (v2 – 1)/2v
x(dv/dx) = [(v2 – 1)/2v] – v
x(dv/dx) = (v2 – 1 – 2v2)/2v
x(dv/dx) = -(1 + v2)/2v
2vdv/(1 + v2) = -(dx/x)
On integrating both sides
∫2vdv/(1 + v2) = -∫(dx/x)
log|1 + v2| = -log|x| + log|c|
log|x(1 + v2)| = log|c|
x(1 + y2/x2) = c
(x2 + y2) = cx
Question 25. Find the equation of the curve which passes through the point (1, 2) and the distance between the foot of the ordinate of the point of contact and the point of intersection of the tangent with x-axis is twice the abscissa of the point of contact.
Solution:
Let us considered
the point of contact of tangent = P(x, y)
and the curve is y = f(x).
The equation of tangent of the curve is given by,
Y – y = (dy/dx)(X – x)
Where (X, Y) is arbitrary point on the tangent.
Putting Y = 0,
0 – y = (dy/dx)(X – x)
(X – x) = -y(dx/dy)
X = x – y(dx/dy)
Coordinates at contact of x-axis = [x – y(dx/dy), 0]
The distance between the foot of the ordinate of the point of
contact and the point of intersection of the tangent with x-axis is equal to 2x.

y(dx/dy) = 2x
(dx/x) = 2(dy/y)
On integrating both sides
∫(dx/x) = 2∫(dy/y)
log|x| = 2log|y| + log|c| …(i)
Curve is passing through (1, 2)
log|1| = 2log|2| + log|c|
log|c| = -2log|2|
On putting the value of log|c| in equation (i)
log|x| = 2log|y| – 2log|2|
log|x| = log|y2/4|
x = (y2/4)
y2 = 4x
Question 26. The normal to a given curve at each point is(x, y) on the curve passes through the point (3, 0). If the curve contains the point (3, 4). Find its equation.
Solution:
Let us considered the point on the curve = P(x, y).
The equation of tangent of the curve is given by,
Y – y = -(dx/dy)(X – x) …(i)
It passes through (3, 0) So,
0 – y = -(dx/dy)(3 – x)
ydy = 3dx – xdx
On integrating both sides
∫ydy = 3∫dx – ∫xdx
(y2/2) = 3x – (x2/2) + c
It passes through (3, 4)
(16/2) = 9 – (9/2) + c …(ii)
c = (16/2) – (9/2)
c = (7/2)
(y2/2) = 3x – (x2/2) + (7/2)
or
y2 = 6x – x2 + 7
Question 27. The rate of increase of bacteria in culture is proportional to the number of bacteria present, and it is found that the number doubles in 6 hours. Prove that the bacteria becomes 8 times at the end of 18 hours.
Solution:
Let us considered
the initial count of bacteria = P0
the count of bacteria at a particular time ‘t’ = P
and the growth of bacteria = g times.
We have,
dP/dt ∝ P
dP/dt = gP
dP/P = gdt
On integrating both sides
∫(dP/P) = g∫dt
Log|P| = gt + c
At t = 0, P = P0
log|P0| = c
Log|P| = gt + log|P0|
Log|P/P0| = gt
Count of bacteria becomes doubled in 6 hours.
At t = 6, P = 2P0
Log|2P0/P0| = 6g
g = Log|2|/6
Log|P/P0| = [Log|2|/6] × t
After t = 18 hours count of bacteria is equal to
Log|P/P0| = [Log|2|/6] × 18
Log|P/P0| = 3Log|2|
Log|P/P0| = Log|2|3
(P/P0) = 8
P = 8P0
Hence proved
Question 28. Radium decomposes at a rate proportional to the quantity of radium present. It is found that in 25 years, approximately 1.1% of a certain quantity of radium has decomposed. Determine approximately how long it will take for one-half of the original amount of radium to decompose?
Solution:
Let us considered
the original amount of radium = P0
and the amount of radium at a particular time ‘t’ = P
We have,
dP/dt ∝ P
(dP/dt) = -kP (Where k is proportional constant)
(dP/P) = -kdt
On integrating both sides
∫(dP/P) = -∫kdt
Log|P| = -kt + c …(i)
At t = 0, P = P0
Log|P0| = 0 + c
c = log|P0|
Log|P| = -kt + Log|P0|
Log|P/P0| = -kt …(ii)
According to the question,
In 25 years bacteria decomposes 1.1%.
So, P = (100 – 1.1)%P0
P = 0.989P0
Log|P/P0| = -kt
Log|0.989| = -25k
k = -(1/25)Log|0.989|
On putting the value of k in equation (ii)
Log|P/P0| = (1/25)Log|0.989| × t
Time ‘T’ for one-half of the original amount of radium(i.e., P0 = P/2)
Log|P0/(P0/2)| = (1/25)Log|0.989| × t
Log|2| = (1/25)Log|0.989| × t
t = (25Log|2|/Log|0.989|)
t = (25×0.69311)/(0.01106)
t = 1566.70
t = 1567 years
Question 29. Show that all curves for which the slope at any point (x, y) on it is (x2 + y2)/2xy are rectangular hyperbola.
Solution:
We have,
(dy/dx) = (x2 + y2)/2xy
The given equation is a homogeneous equation,
So, let us considered, y = vx
On differentiating both sides we have,
(dy/dx) = v + x(dv/dx)
(dy/dx) = (x2 + v2x2)/2xvx
v + x(dv/dx) = (x2 + v2x2)/2xvx
v + x(dv/dx) = (1 + v2)/2v
x(dv/dx) = [(1 + v2)/2v] – v
x(dv/dx) = (1 + v2 – 2v2)/2v
x(dv/dx) = (1 – v2)/2v
2vdv/(1 – v2) = (dx/x)
On integrating both sides
∫2vdv/(1 – v2) = ∫(dx/x)
-log|1 – v2| = log|x| – log|c|
-log|(1 – v2)| = -[log|c| – log|x|]
-log|(1 – v2)| = -log|c/x|
(1 – v2) = c/x
(1 – y2/x2) = c/x
(x2 – y2)/x2 = c/x
(x2 – y2) = cx
This is the required equation of a rectangular hyperbola.
Question 30. The slope of the tangent at each point of a curve is equal to the sum of the coordinates of the point. Find the curve that passes through the origin.
Solution:
The equation of tangent of the curve is given by,
(dy/dx) = x + y
(dy/dx) – y = x
The given equation is a linear differential equation of the form
(dx/dy) + Px = Q
Where, P = -1, Q = -x
So, I.F = e∫Pdx
= e∫-dx
= e-x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx+c
y(e-x) = ∫(x).(e-x)dy+c
y(e-x) = x∫e-xdx-∫{(dx/dx)∫e-xdx}dx+c
y(e-x) = -xe-xx + ∫e-x + c
y(e-x) = -xe-x – e-x + c
y(e-x) = -e-x(x + 1) + c (i)
Since the curve is passing through origin. So,
0 = -e-0(1) + c
c = 1
On putting the value of c in equation (i)
y(e-x) = -e-x(x + 1) + c
(x + y + 1) = c.ex
Put c = 1
x + y + 1 = ex
Question 31. Find the equation of the curve passing through the point (0, 1) if the slope of tangent to the current each of its point is equal to the sum of the abscissa and product of the abscissa and the ordinate of the point.
Solution:
The equation of tangent of the curve is given by
(dy/dx) = x + xy
(dy/dx) – xy = x
The given equation is a linear differential equation of the form
(dx/dy) + Px = Q
Where, P = -x, Q = x
So, I.F = e∫Pdx
= e-∫xdx
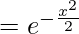
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
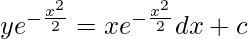
Let,
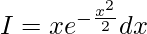
Let,x2/2 = z
On differentiating both sides,
xdx = dz
I = ∫e-zdz
I = -e-z
So,
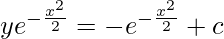
Curve is passing through point (0, 1).
1e0 = -e0 + c
c = 2
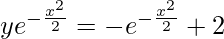
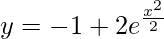
Question 32. The slope of a curve at each of its points is equal to the square of the abscissa of the point. Find the particular curve through the point (-1, 1).
Solution:
According to the question,
(dy/dx) = x2
dy = x2dx
On integrating both sides
∫dy = ∫x2dx
y = (x3/3) + c …(i)
Curve is passing through the point (-1, 1)
1 = -(1/3) + c
c = (4/3)
On putting the value of c in equation (i)
y = (x3/3) + (4/3)
3y = x3 + 4
Question 33. Find the equation of the curve that passes through the point (0, a) and as such at any point (x, y) on it, the product of its slope and the ordinate is equal to the abscissa.
Solution:
According to the question,
y(dy/dx) = x
dy = x2dx
On integrating both sides
∫ydy = ∫xdx
(y2/2) = (x2/2) + c …(i)
Curve is passing through the point (0, a)
(a2/2) = c
c = a2/2
On putting the value of c in equation (i)
(y2/2) = (x2/2) + (a2/2)
x2 – y2 = -a2
Question 34. The x-intercept of the tangent line to a curve is equal to the ordinate of the point contact. Find the particular curve through the point (1, 1).
Solution:
Slope at any point is given by P = (dy/dx)
According to the question,
Slope at any point is equal to ordinate
We have,
(dy/dx) = y
dy/y = dx
On integrating both sides
∫(dy/y) = ∫(dx)
log|y| = x + log|c|
log|y| = log|ex| + log|c|
y = c.ex …(i)
Curve is passing through the point (1, 1)
1 = c.e
c = e-1
On putting the value of c in equation (i)
y = ex.e-1
y = e(x-1)
Share your thoughts in the comments
Please Login to comment...