Class 12 RD Sharma Solutions – Chapter 21 Areas of Bounded Regions – Exercise 21.1 | Set 1
Last Updated :
04 Feb, 2022
Question 1. Using integration, find the area of region bounded between the line x = 2 and parabola y2 = 8x
Solution:
Here,
Given equations are:
x = 2 ……..(1)
y2 = 8x ……..(2)
Here,
Equation (1) represents a line parallel to y-axis and equation (2) represents a parabola with vertex at origin and x-axis,
Here is the rough sketch

We have to find the area of shaded region. We sliced it in vertical rectangle width of rectangle = △x,
Length = (y – 0) = y
Area of rectangle = y△x
This rectangle can move horizontal from x = 0 to x = 2
Required area = Shaded region OCBO
= 2 (Shaded region OABO)
= ![Rendered by QuickLaTeX.com \displaystyle =2\int_0^2y\ dx\\ =2\times2\sqrt2\int_0^2\sqrt{x}\ dx\\ =4\sqrt2\left[\frac{2}{3}\times\sqrt{x}\right]_0^2\\ =4\sqrt2\left[\left(\frac{2}{3}\times2\sqrt2\right)-\left(\frac{2}{3}\right)\times0\sqrt0\right]\\ =4\sqrt2\left(\frac{4\sqrt2}{3}\right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-821d02ded30051624b641f6583b21f28_l3.png)
Required area = 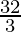 square units.
square units.
Question 2. Using integration, find the area of the region bounded by the line y – 1 = x, the x-axis and the ordinates x = -2 and x = 3.
Solution:
The find area of region bounded by x-axis the ordinates x = -2 and x = 3
y – 1 = x ………….(1)
Equation (1) is a line that meets at axes at (0, 1) and (-1, 0)
Here, is the rough sketch

Required area is enclosed between the lines.
Required area = Region ABCA + Region ADEA
![Rendered by QuickLaTeX.com \displaystyle A=\int^3_{-1}y\ dx + \left|\int^{-1}_{-2}y\ dx\right|\\ =\int_{-1}^{3}(x+1)dx+\left|\int_{-2}^{-1}(x+1)dx\right|\\ =\left(\frac{x^2}{2}+x\right)_{-1}^3+\left|\left(\frac{x^2}{2}+x\right)_{-2}^{-1}\right|\\ =\left[\left(\frac{9}{3}+3\right)-\left(\frac{1}{2}-1\right)\right]+\left|\left(\frac{1}{2}-1(2-2)\right)\right|\\ =\left[\frac{15}{2}+\frac{1}{2}\right]+\left|-\frac{1}{2}\right|\\ =8+\frac{1}{2}\\ A=\frac{17}{2}\ square\ units.](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a38870871201884a18f5d1bbe42cd5c3_l3.png)
Question 3. Find the area of the region bounded by the parabola y2 = 4ax and the line x = a
Solution:
Here we have to find the area of the region that is bounded by
x = a ………(1)
and
y2 = 4a ………(2)
Equation (1) represents a line parallel to y-axis and equation (2) represent a parabola with vertex at origin and axis as x-axis.
Here, is the rough sketch

Here we have to find area between the region,
Thus, slice it in rectangles of
Width = △x
Length = y – 0 = y
Area of rectangle = y△x
This assumed triangle can go from x = 0 to x = a.
Required area = Region OCBO
= 2 (Region OABO)
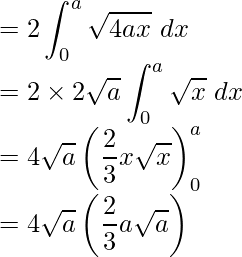
Required area = 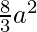 square units
square units
Question 4. Find the area lying above the x-axis and under the parabola y = 4x – x2.
Solution:
We have to find here the bounded area by x-axis and parabola
y = 4x – x2
x2 – 4x +4 = -y + 4
(x – 2)2 = -(y – 4) ……….(1)
Equation (1) represent a downward parabola with vertex (2, 4) and passing through (0, 0) and (0, 4).
Here is the rough sketch

Here the shaded region represents the required area.
We slice the region in approximation rectangles
Width = △x
Length = y – 0 = y
Area of rectangle = y△x
This approximation rectangle slide from x = 0 to x = a
Thus,
Required area = Region OABO
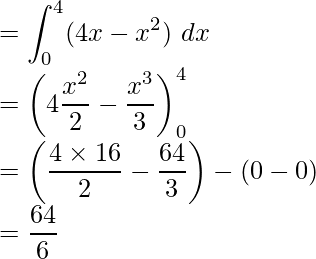
Required area = 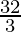 square units
square units
Question 5. Draw a rough sketch to indicate the region bounded between the curve y2 = 4x and the line x = 3. Also, find the area of this region.
Solution:
We have to find area bounded by
y2 = 4x ……..(1)
and
x = 3 ………..(2)
Equation (1) represents a parabola with vertex at origin and axis as x-axis and equation (2) represents a line parallel to y-axis
Here is the rough sketch

Shaded region represents the required area that we have sliced in the form of a rectangle of
Width = △x
Length = y – 0 = y
This approximation rectangle slide from x = 0 to x = 3
Required area = Region OCBO
= 2(Region OABO)
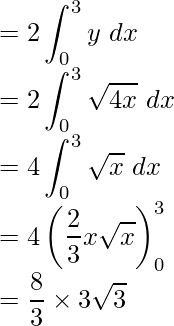
Required area = 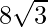 square units
square units
Question 6. Make a rough sketch of the graph of the function y = 4 – x2, 0 ≤ x ≤ 2 and determine the area enclosed by the curve, the x-axis, and the line x = 0 and x = 2.
Solution:
Here, we will find the area enclosed by
y = 4 – x2
x2 = -(y – 4) ……….(1)
x = 0 ………(2)
x = 2 ……….(3)
Equation (1) represents a downward parabola with vertex at (0, 4) and passing through (2, 0), (-2, 0). Equation (2) represents y-axis and equation (3) represents a line parallel to y-axis.
Here’s a rough sketch

Shaded region represents the required area that we have sliced in the form of a rectangle of
Width = △x
length = y – 0 = y
This approximation rectangle slide from x = 0 to x = 2
Required area = Region OABO
![Rendered by QuickLaTeX.com \displaystyle =\int_0^2(4-x^2)\ dx\\ =\left(4x-\frac{x^3}{3}\right)_0^2\\ =\left[4(2)-\frac{(2)^3}{3}\right]-[0]\\ =\left[\frac{24-8}{3}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c747aff426265e97fcc16117ddb49595_l3.png)
Required area = 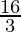 square units.
square units.
Question 7. Sketch the graph of 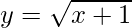 in [0, 4] and determine the area of the region enclosed by the curve, the x-axis and the line x = 0 and x = 4.
in [0, 4] and determine the area of the region enclosed by the curve, the x-axis and the line x = 0 and x = 4.
Solution:
Here, we will find the area enclosed by x-axis and
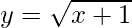
y2 = x + 1 …….(1)
x = 0 ………(2)
x = 4 ………(3)
Equation (1) represents a parabola with vertex at (-1, 0) and passing through (0, 1) and (0, -1). Equation (2) represents y-axis and equation (3) represents a line parallel to y-axis passing through (4, 0).
Thus, here is the rough sketch;

Shaded region represents the required area that we have sliced in the form of a rectangle of
Width = △x
Length = y – 0 = y
Area of rectangle = y△x
This approximation rectangle slide from x = 0 to x = 4
Required area = Region OECDO
![Rendered by QuickLaTeX.com \displaystyle =\int_0^4y\ dx\\ =\int_0^4\sqrt{x+1}\ dx\\ =\left(\frac{2}{3}(x+1)\sqrt{x+1}\right)_0^4\\ =\frac{2}{3}[((4+1)\sqrt{4+1})-((0+1)\sqrt{0+1})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d40e147ba2e28244aaf174140bf79d14_l3.png)
Required area = ![Rendered by QuickLaTeX.com \frac{2}{3}[5\sqrt5-1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-63bfa0b3ad2b4194b27cd1dcfbb4dced_l3.png) square units or
square units or ![Rendered by QuickLaTeX.com \frac{2}{3}\left[5^\frac{3}{2}-1\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8d40e2c2cffa90d4ab9129d077824e2e_l3.png) square units.
square units.
Question 8. Find the area under the curve 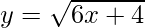 above x-axis from x = 0 to x = 2. Draw a sketch of the curve also.
above x-axis from x = 0 to x = 2. Draw a sketch of the curve also.
Solution:
Here, we will find the area enclosed by x-axis
x = 0,
x = 2 ………(1)
y2 = 6x + 4 ……….(2)
Equation (1) represents y-axis and a line parallel to y-axis passing through (2, 0). Equation (2) represents a parabola with vertex at 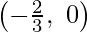 and passes through the points (0, 2) , ( 0, -2).
and passes through the points (0, 2) , ( 0, -2).
Thus, here is the rough sketch;

Shaded region represents the required area that we have sliced in the form of a rectangle of
Width = △x
Length = y – 0 = y
Area of rectangle = y△x
This approximation rectangle slide from x = 0 to x = 2,
Required area = Region OABCO
![Rendered by QuickLaTeX.com \displaystyle =\int_0^2\sqrt{6x+4}\ dx\\ =\left(\frac{2}{3}\frac{(6x+4)\sqrt{6x+4}}{6}\right)_0^2\\ =\frac{1}{9}[((12+4)\sqrt{12+4})-((0+4)\sqrt{0+4})]\\ =\frac{1}{9}[16\sqrt{16}-4\sqrt{4}]\\ =\frac{1}{9}(64-8)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b87798388077b98e3eedf33b24325437_l3.png)
Required area = 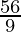 square units.
square units.
Question 9. Draw the rough sketch of y2 + 1 = x, x ≤ 2. Find the area enclosed by the curve and the line x = 2.
Solution:
Here, we will find the area enclosed by x-axis
y2 = x + 1 ……….(1)
and
x = 2 ……………(2)
Equation (1) is a parabola with vertex at (0, 1) and axis as x-axis.
Equation (2) represents a line parallel to y-axis passing through (2, 0)
Thus, here is the rough sketch;

Shaded region represents the required area that we have sliced in the form of a rectangle of
Width = △x
Length = y – 0 = y
Area of rectangle = y△x
This approximation rectangle slide from x = 0 to x = 2,
Required area = Region ABCA
= 2(Region AOCA)
![Rendered by QuickLaTeX.com \displaystyle =2\int_1^2y\ dx\\ =2\int_1^2\sqrt{x-1}\ dx\\ =2\left(\frac{2}{3}(x-1)\times\sqrt{x-1}^2\right)_1^2\\ =\frac{4}{3}[((2-1)\sqrt{2-1})-((1-1)\sqrt{1-1})]\\ =\frac{4}{3}(1-0)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0b8caf053c8117eed957b1baa9bb24c0_l3.png)
Required area = 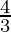 square units.
square units.
Question 10. Draw a rough sketch of the graph of the curve 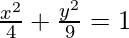 and evaluate the area of the region under the curve and above the x-axis
and evaluate the area of the region under the curve and above the x-axis
Solution:

Here, we can observe that ellipse is symmetrical about x-axis.
Area bounded by ellipse = ![Rendered by QuickLaTeX.com \displaystyle =2\int_0^2 y\ dx\\ = 2\int_0^23\sqrt{1-\frac{x^2}{4}}\ dx\\ =3\int\sqrt{4-x^2}\ dx\\ =3\left[\frac{x}{2}\sqrt{4-x^2}+\frac{4}{2}sin^{-1}\frac{x}{2}\right]_0^2\\ =3[1(0)+2sin^{-1}-0-2sin^{-1}(0)]\\ =3[\pi]\\ =3\pi\ sq.\ units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cd10c90185ff60923b7d4931a13db35c_l3.png)
Share your thoughts in the comments
Please Login to comment...