Question 1. Solve the following system of equations by matrix method:
(i) 5x + 7y + 2 = 0
4x + 6y + 3 = 0
Solution:
The given system of equations can be written in matrix form as,
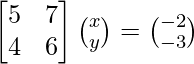
AX = B
Here,
A =  , X =
, X = 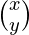 and B =
and B = 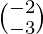
Now,
|A| = 
= 30 – 28
= 2
The given system has a unique solution given by, X = A-1 B.
Let Cij be the cofactor of the elements aij in A.
C11 = (-1)1+1 (6) = 6, C12 = (-1)1+2 (4) = -4, C21 = -12+1 (7) = -7 and C22 = (-1)2+2 (5) = 5
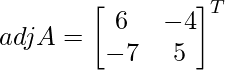
= 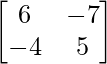
A-1 = 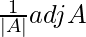
A-1 = 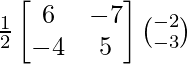
So, X = A-1 B
= 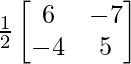
= 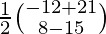
=> 
Therefore, x = 9/2 and y = -7/2.
(ii) 5x + 2y = 3
3x + 2y = 5
Solution:
The given system of equations can be written in matrix form as,
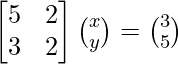
AX = B
Here,
A = 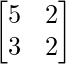 , X =
, X = 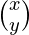 and B =
and B = 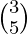
Now,
|A| = 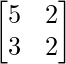
= 10 – 6
= 4
The given system has a unique solution given by, X = A-1 B
Let Cij be the cofactor of the elements aij in A.
C11 = -11+1 (2) = 2, C12 = (-1)1+2 (3) = – 3, C21 = (-1)2+1 (2) = – 2 and C22 = (-1)2+2 (5) = 5
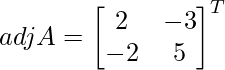
= 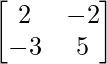
A-1 = 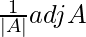
= 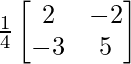
Now, X = A-1 B
= 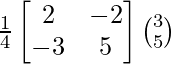
= 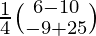
=> 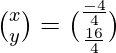
Therefore, x = – 1 and y = 4.
(iii) 3x + 4y − 5 = 0
x − y + 3 = 0
Solution:
The given system of equations can be written in matrix form as,
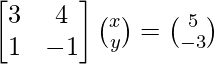
AX = B
Here,
A = 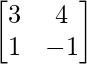 , X =
, X = 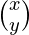 and B =
and B = 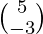
Now,
|A| = 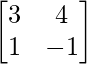
= – 3 – 4
= -7
So, the given system has a unique solution given by, X = A-1 B
Let Cij be the cofactors of the elements aij in A.
C11 = (-1)1+1 (1) = -1, C12 = (-1)1+2 (-1) = 1, C21 = (-1)2+1 (4) = -4 and C22 = (-1)2+2 (3) = 3
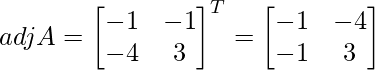
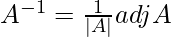
= 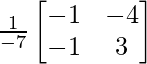
Now, X = A-1 B
= 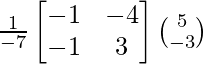
= 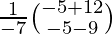
=> 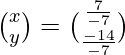
Therefore, x = -1 and y = 2.
(iv) 3x + y = 19
3x − y = 23
Solution:
The given system of equations can be written in matrix form as,
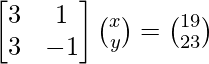
AX = B
Here,
A = 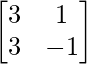 , X =
, X = 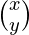 and B =
and B = 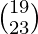
Now,
|A| = 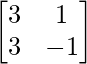
= – 3 – 3
= -6
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
C11 = (-1)1+1 (-1) = -1, C12 = (-1)1+2 (3) = -3, C21 = (-1)2+1 (1) = -4 and C22 = (-1)2+2 (3) = 3
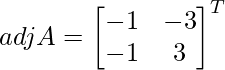
= 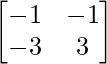
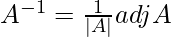
= 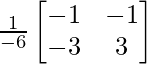
Now, X = A-1 B
= 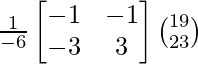
= 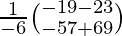
=> 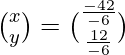
Therefore, x = 7 and y = -2.
(v) 3x + 7y = 4
x + 2y = −1
Solution:
The given system of equations can be written in matrix form as,
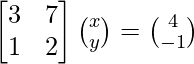
AX = B
Here,
A =  , X =
, X = 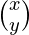 and B =
and B = 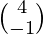
Now,
|A| = 
= 6 – 7
= -1
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
C11 = (-1)1+1 (2) = 2, C12 = (-1)1+2 (1) = -1, C21 = (-1)2+1 (7) = -7 and C22 = (-1)2+2 (3) = 3
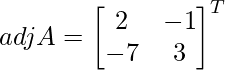
= 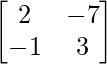
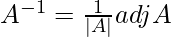
= 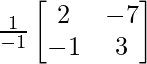
X = A-1 B
= 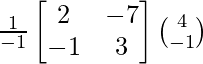
= 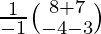
=> 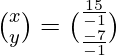
Therefore x = – 15 and y = 7.
(vi) 3x + y = 7
5x + 3y = 12
Solution:
The given system of equations can be written in matrix form as,
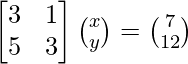
AX = B
Here,
A = 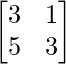 , X =
, X = 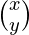 and B =
and B = 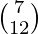
Now,
|A| = 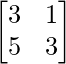
= 9 – 5
= 4
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
C11 = (-1)1+1 (3) = 3, C12 = (-1)1+2 (5) = -5, C21 = (-1)2+1 (1) = -1 and C22 = (-1)2+2 (3) = 3
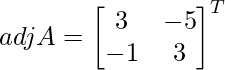
= 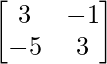
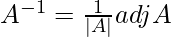
= 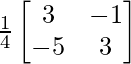
X = A-1 B
= 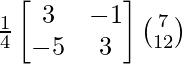
= 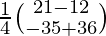
=> 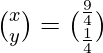
Therefore x = 9/4 and y = 1/4.
Question 2. Solve the following system of equations by matrix method:
(i) x + y − z = 3
2x + 3y + z = 10
3x − y − 7z = 1
Solution:
A = 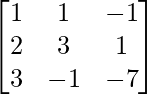
|A| = 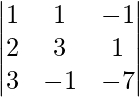
= 1 (- 21 + 1) – 1(-14 – 3) – 1(-2 – 9)
= – 20 + 17 + 11
= 8
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactor of the elements aij in A.
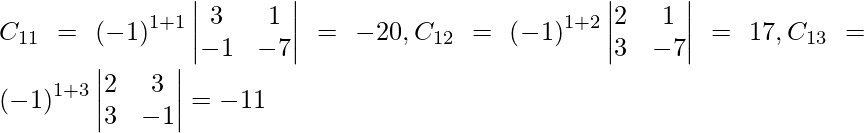
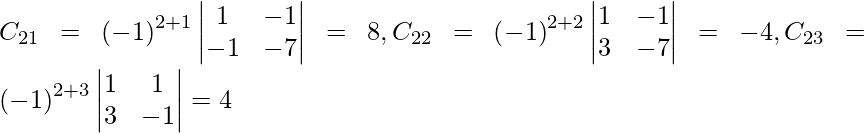
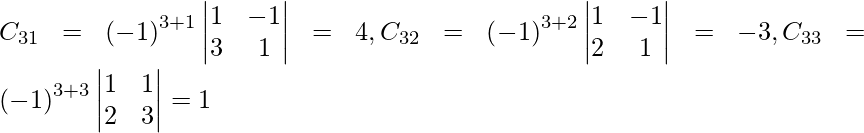
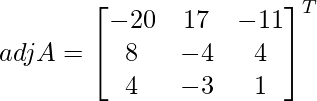
= 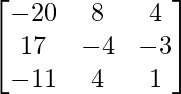
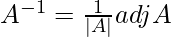
= 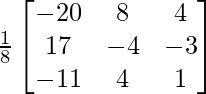
X = A-1 B
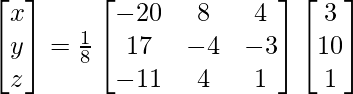
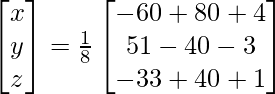
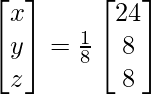
=> x = 24/8, y = 8/8 and z = 8/8
Therefore, x = 3, y = 1 and z = 1.
(ii) x + y + z = 3
2x − y + z = − 1
2x + y − 3z = − 9
Solution:
A = 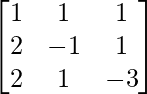
|A| = 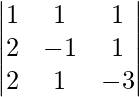
= 1 (3 – 1) – 1 (-6 – 2) + 1 (2 + 2)
= 2 + 8 + 4
= 14
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
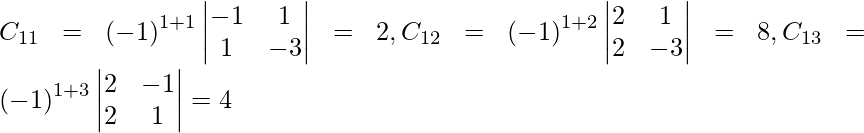
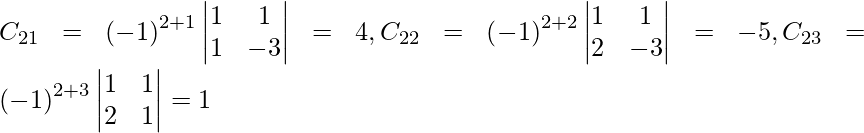
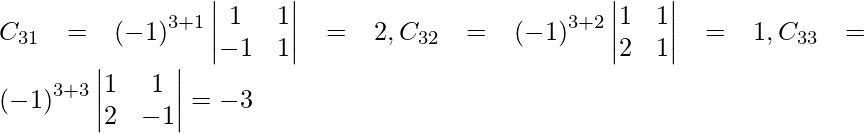
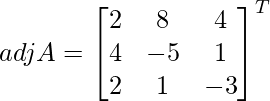
= 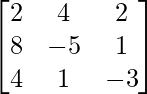
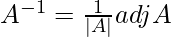
= 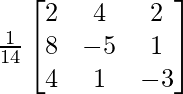
Now, X = A-1 B
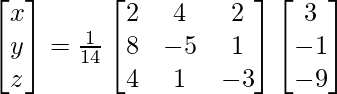
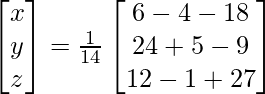
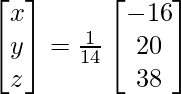
=> x = -16/14, y = 20/14 and z = 38/14
Therefore, x = -8/7, y = 10/7 and z = 19/7.
(iii) 6x − 12y + 25z = 4
4x + 15y − 20z = 3
2x + 18y + 15z = 10
Solution:
A = 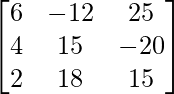
|A| = 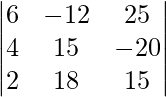
= 6 (225 + 360) + 12 (60 + 40) + 25 (72 – 30)
= 3510 + 1200 + 1050
= 5760
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
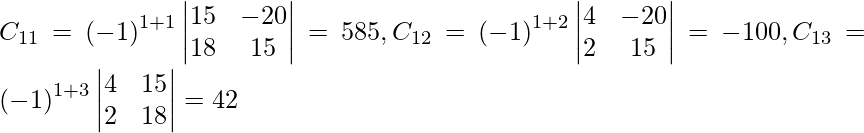
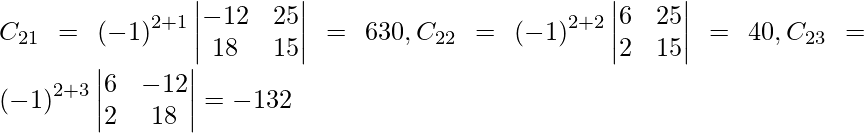
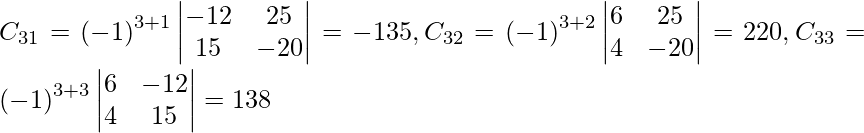
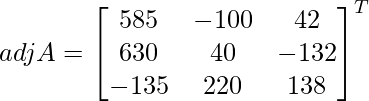
= 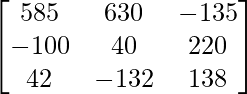
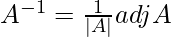
= 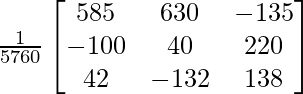
Now, X = A-1 B
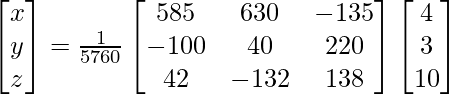
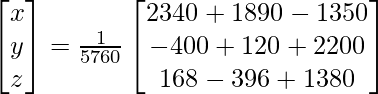
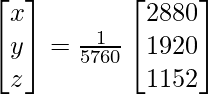
=> x = 2880/5760, y = 1920/5760 and z = 1152/5760
Therefore x = 1/2, y = 1/3 and z = 1/5.
(iv) 3x + 4y + 7z = 14
2x − y + 3z = 4
x + 2y − 3z = 0
Solution:
A = 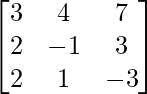
|A| = 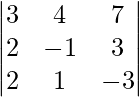
= 3 (3 – 3) – 4 (- 6 – 6) + 7 (2 + 2)
= 0 + 48 + 28
= 76
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
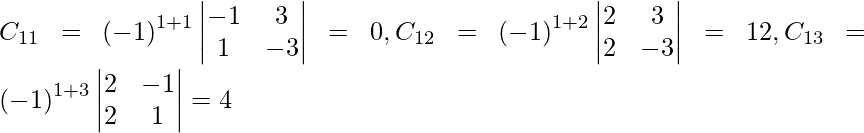
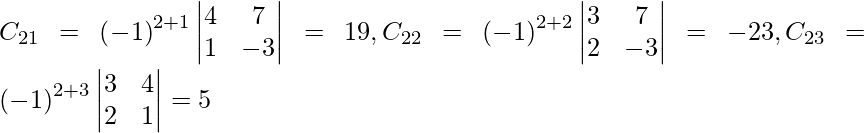
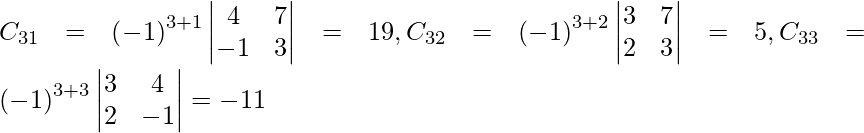
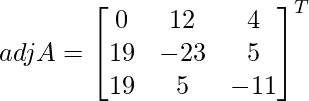
= 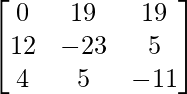
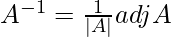
= 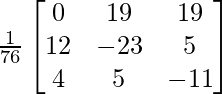
Now, X = A-1 B
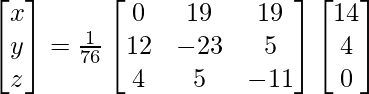
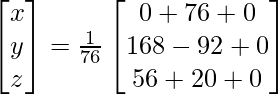
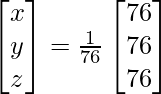
=> x = 76/76, y = 76/76 and z = 76/76
Therefore x = 1, y = 1 and z = 1.
(v) 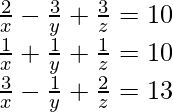
Solution:
Let 1/x be a, 1/y be b and 1/z be c.
Here,
A = 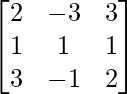
|A| = 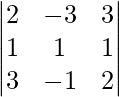
= 2 (2 + 1) + 3 (2 – 3) + 3 (-1 – 3)
= 6 – 3 – 12
= -9
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
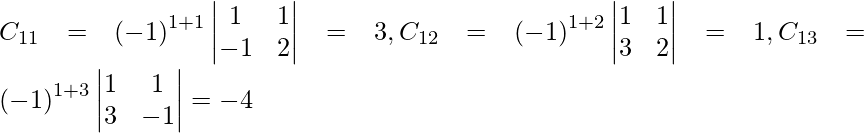
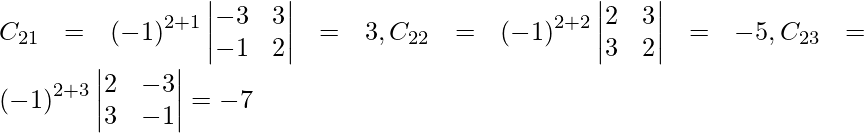
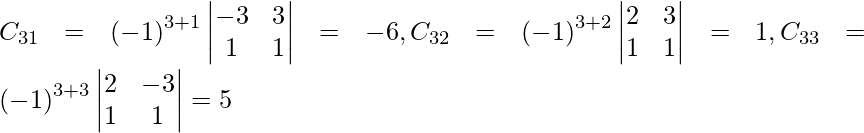
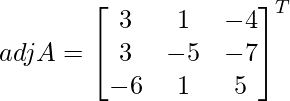
= 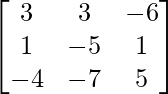
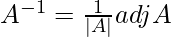
= 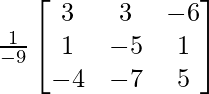
X = A-1 B
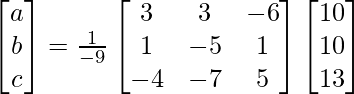
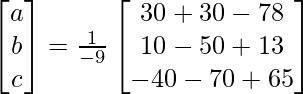
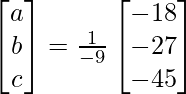
=> x = 1/a = – 9/-18, y = 1/b = – 9/- 27 and z = 1/c = -9/-45
Therefore x = 1/2, y = 1/3 and z = 1/5.
(vi) 5x + 3y + z = 16
2x + y + 3z = 19
x + 2y + 4z = 25
Solution:
A = 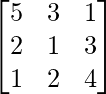
|A| = 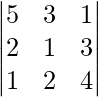
= 5 (4 – 6) – 3 (8 – 3) + 1 (4 – 1)
= -10 – 15 + 3
= – 22
So, the given system has a unique solution given by X = A-1 B.
Let Cij be the cofactors of the elements aij in A.
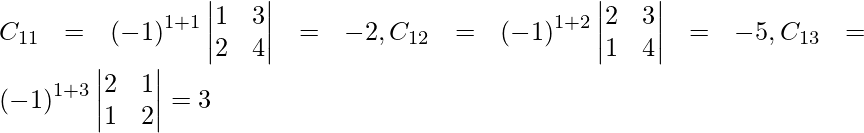
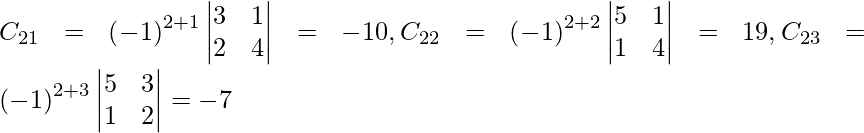
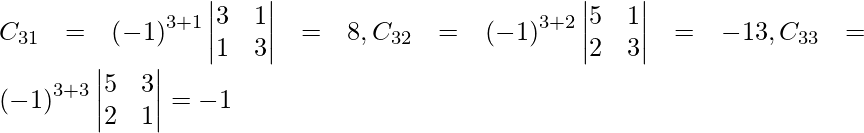
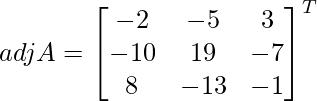
= 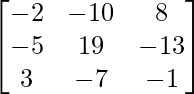
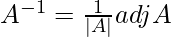
= 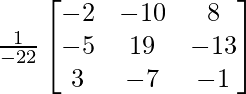
X = A-1 B
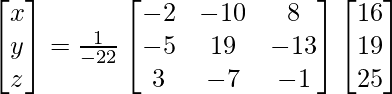
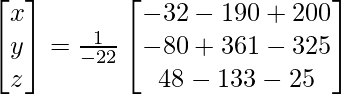
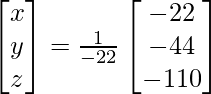
=> x = – 22/- 22, y = – 44/- 22 and z = -110/-22
Therefore x = 1, y = 2 and z = 5.
(vii) 3x + 4y + 2z = 8
2y − 3z = 3
x − 2y + 6z = −2
Solution:
A = 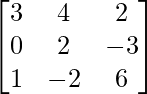
|A| = 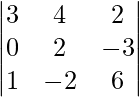
= 3 (12 – 6) – 4 (0 + 3) + 2 (0 – 2)
= 18 – 12 – 4
= 2
Let Cij be the cofactors of the elements aij in A.
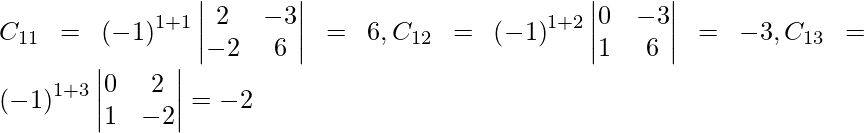
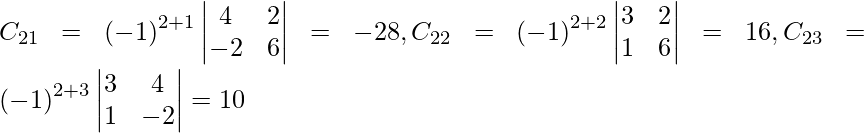
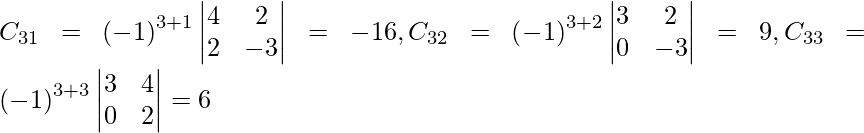
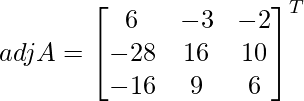
= 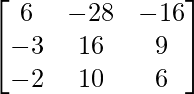
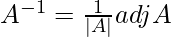
= 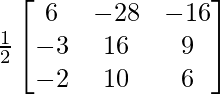
Now X = A-1 B
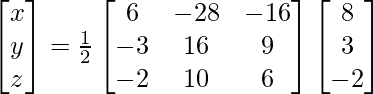
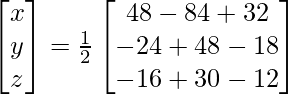
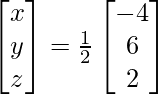
=> x = -4/2, y = 6/2 and z = 2/2
Therefore x = -2, y = 3 and z = 1.
(viii) 2x + y + z = 2
x + 3y − z = 5
3x + y − 2z = 6
Solution:
Here,
A = 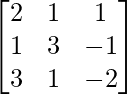
|A| = 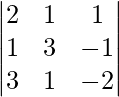
= – 10 – 1 – 8
= -19
Let Cij be the cofactors of the elements aij in A.
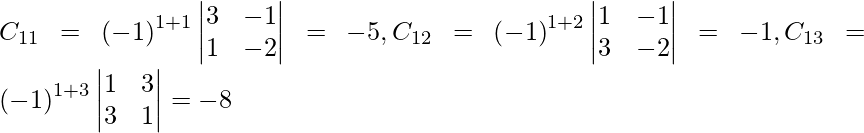
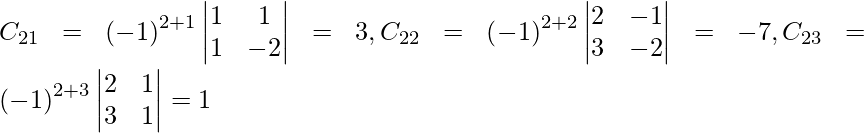
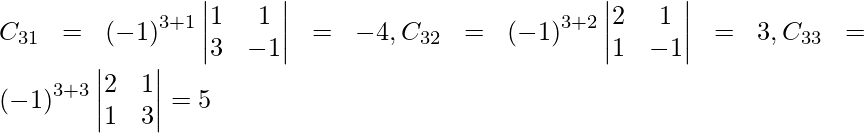
adj A = 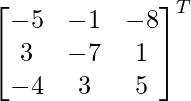
= 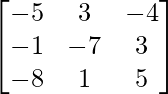
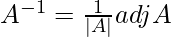
= 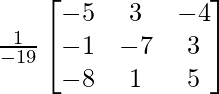
X = A-1 B
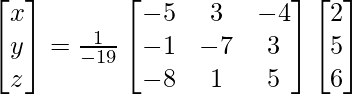
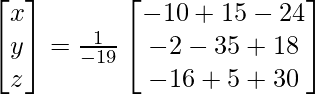
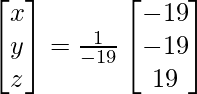
x = -19/-19, y = -19/-19 and z = 19/-19
Therefore x = 1, y = 1 and z = – 1.
(ix) 2x + 6y = 2
3x − z = −8
2x − y + z = −3
Solution:
A = 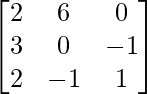
|A| = 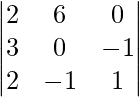
= 2 (0 – 1) – 6 (3 + 2) + 0 (-3 + 0)
= -2 – 30
= – 32
Let Cij be the cofactors of the elements aij in A.
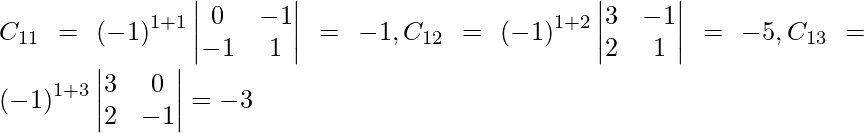
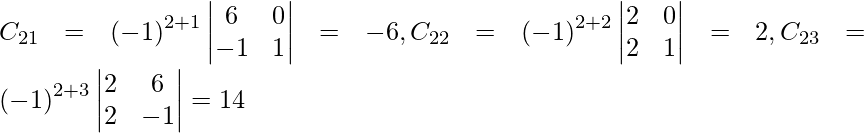
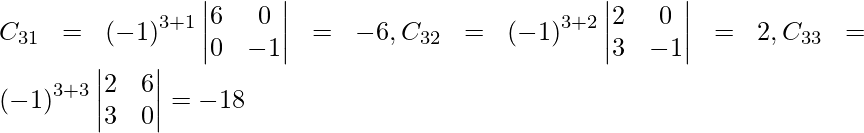
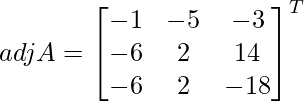
= 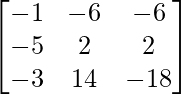
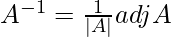
= 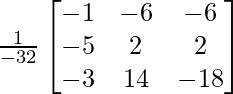
X = A-1 B
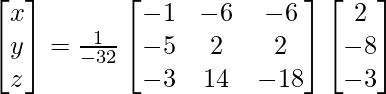
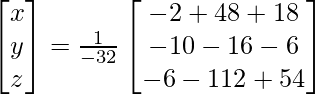
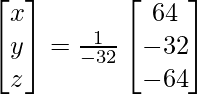
=> x = 64/-32, y = -32/-32 and z = -64/-32
Therefore x = – 2, y = 1 and z = 2.
(x) x − y + z = 2
2x − y = 0
2y − z = 1
Solution:
A = 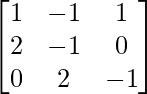
|A| = 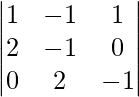
= 1 (1 – 0) + 1 (-2 – 0) + 1(4 – 0)
= 1 – 2 + 4
= 3
Let Cij be the cofactors of the elements aij in A.
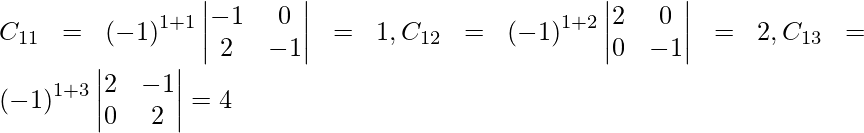
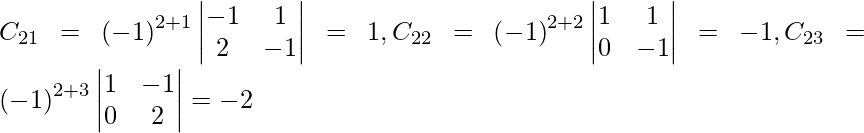
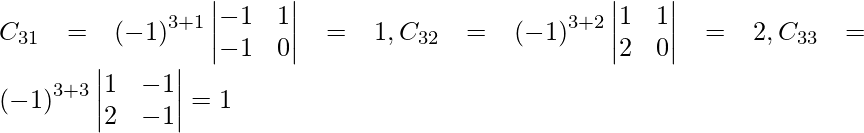
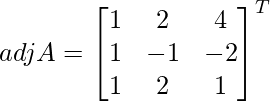
= 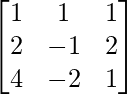
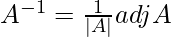
= 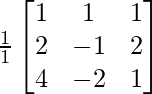
X = A-1 B
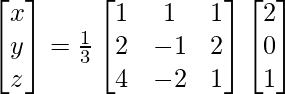
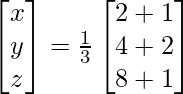
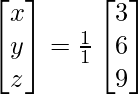
=> x = 3/3, y = 6/3 and z = 9/3
Therefore x = 1, y = 2 and z = 3.
(xi) 8x + 4y + 3z = 18
2x + y +z = 5
x + 2y + z = 5
Solution:
A = 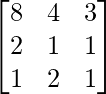
|A| = 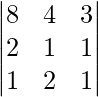
= 8 (1 – 2) – 4 (2 – 1) + 3(4 – 1)
= – 8 – 4 + 9
= -3
Let Cij be the cofactors of the elements aij in A.
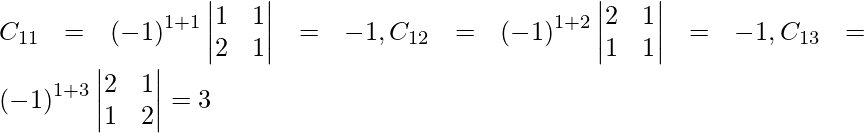
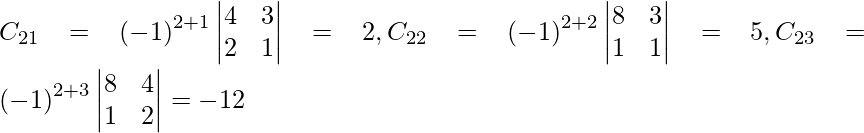
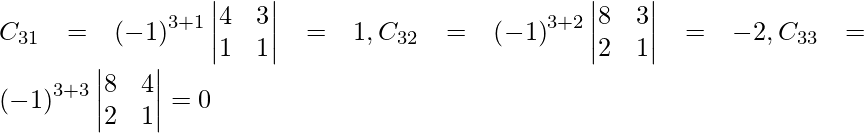
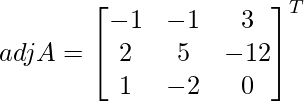
= 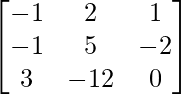
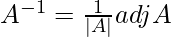
= 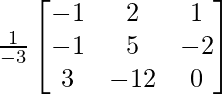
X = A-1 B
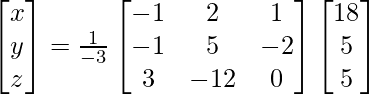
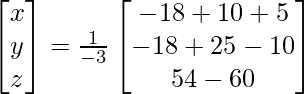
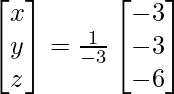
=> x = -3/-3, y = -3/-3 and z = -6/-3
Therefore x = 1, y = 1 and z = 2.
(xii) x + y + z = 6
x + 2z = 7
3x + y + z = 12
Solution:
A = 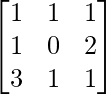
|A| = 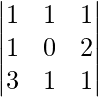
= 1 (0 – 2) – 1 (1 – 6) + 1(1 – 0)
= – 2 + 5 + 1
= 4
Let Cij be the cofactors of the elements aij in A.
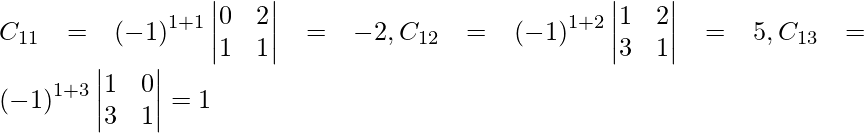
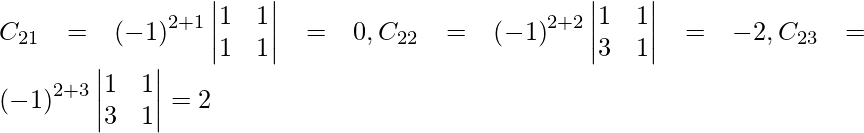
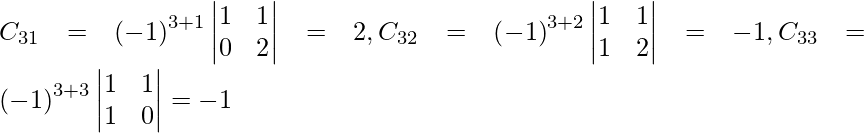
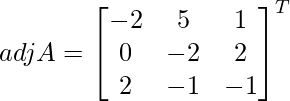
= 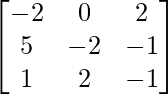
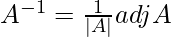
= 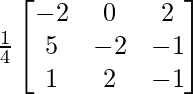
X = A-1 B
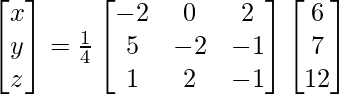
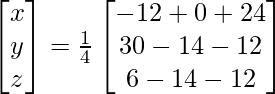
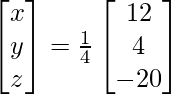
=> x = 12/4, y = 4/4 and z = -20/4
Therefore x = 3, y = 1 and z = – 5.
(xiii) 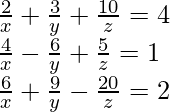 , x, y, z ≠ 0
, x, y, z ≠ 0
Solution:
Let 1/x be a, 1/y be b and 1/z be c.
Here,
A = 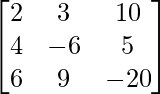
|A| = 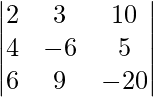
= 2 (120 – 45) – 3 (-80 – 30) + 10 (36 + 36)
= 150 + 330 + 720
= 1200
Let Cij be the cofactors of the elements aij in A.
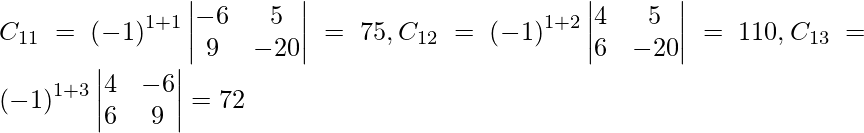
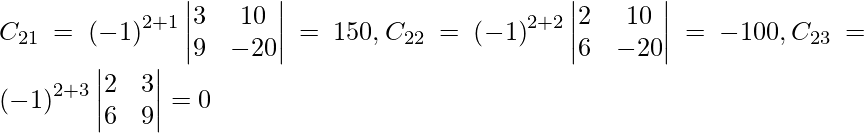
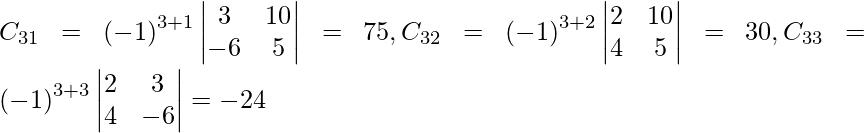
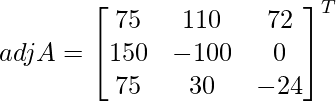
= 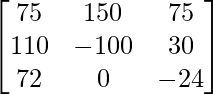
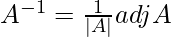
= 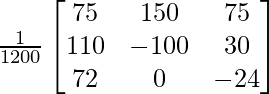
X = A-1 B
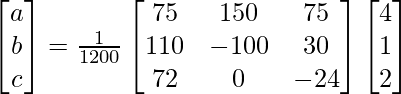
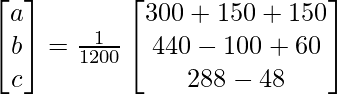
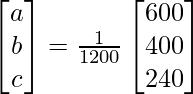
=> x = 1/a = 1200/600, y = 1/b = 1200/400 and z = 1/c = 1200/240
Therefore x = 2, y = 3 and z = 5.
(xiv) x − y + 2z = 7
3x + 4y − 5z = −5
2x − y + 3z = 12
Solution:
A = 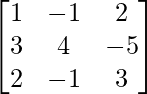
|A| = 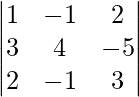
= 1 (12 – 5) + 1 (9 + 10) + 2 (-3 – 8)
= 7 + 19 – 22
= 4
Let Cij be the cofactors of the elements aij in A.
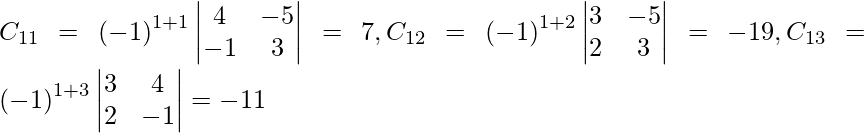
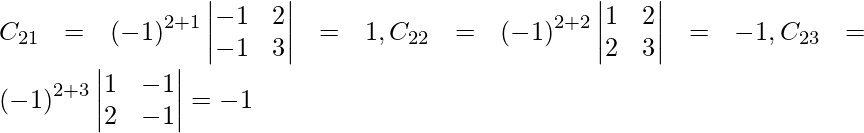
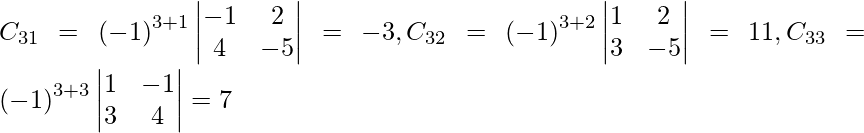
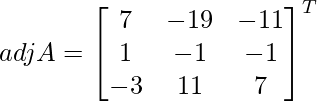
= 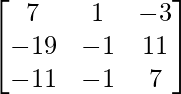
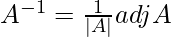
= 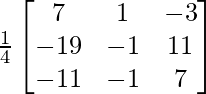
X = A-1 B
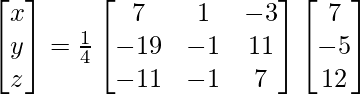
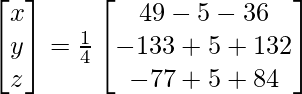
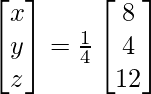
=> x = 8/4, y = 4/4 and z = 12/4
Therefore x = 2, y = 1 and z = 3.
Question 3. Show that the following systems of linear equations is consistent:
(i) 6x + 4y = 2
9x + 6y = 3
Solution:
Here,
6x + 4y = 2
9x + 6y = 3
We know, AX = B
A = 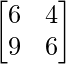 , X =
, X = 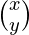 and B =
and B = 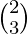
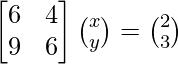
|A| = 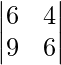
= 36 – 36
= 0
Let Cij be the cofactors of the elements aij in A.
C11 = 6, C12 = -9, C21 = -4 and C22 = 6
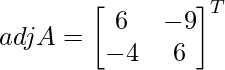
= 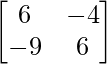
(adj A) B = 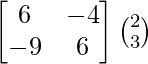
= 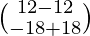
= 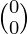
Therefore, the system is consistent and has infinitely many solutions.
Hence proved.
(ii) 2x + 3y = 5
6x + 9y = 15
Solution:
Here,
2x + 3y = 5
6x + 9y = 15
We know, AX = B
A = 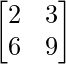 , X =
, X = 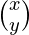 and B =
and B = 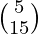
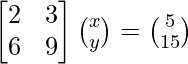
|A| = 
= 18 – 18
= 0
Let Cij be the cofactors of the elements aij in A.
C11 = 9, C12 = -6, C21 = -3 and C22 = 2
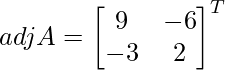
= 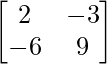
(adj A) B = 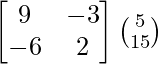
= 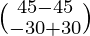
= 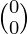
Therefore, the system is consistent and has infinitely many solutions.
Hence proved.
(iii) 5x + 3y + 7z = 4
3x + 26y + 2z = 9
7x + 2y + 10z = 5
Solution:
Here,
5x + 3y + 7z = 4
3x + 26y + 2z = 9
7x + 2y + 10z = 5
We know, AX = B
A = 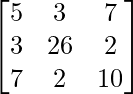 , X =
, X = 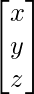 and B =
and B = 
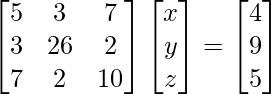
|A| = 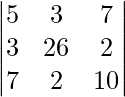
= 1280 – 48 – 1232\]
= 0
Let Cij be the cofactors of the elements aij in A.
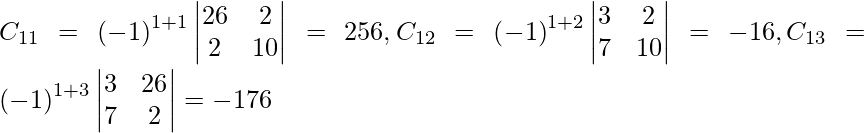
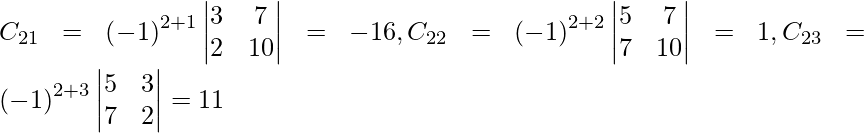
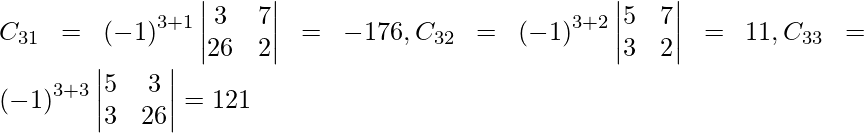
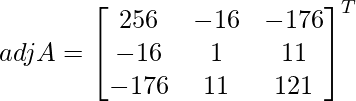
= 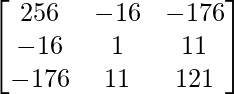
(adj A)B = 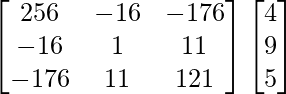
= 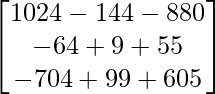
= 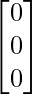
Therefore, the system is consistent and has infinitely many solutions.
Hence proved.
(iv) x − y + z = 3
2x + y − z = 2
−x −2y + 2z = 1
Solution:
Here,
x − y + z = 3
2x + y − z = 2
−x −2y + 2z = 1
We know, AX = B
A = 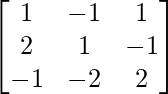 , X =
, X = 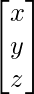 and B =
and B = 
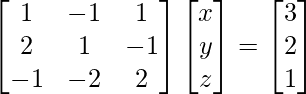
|A| = 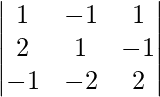
= 1\left( 2 – 2 \right) + 1\left( 4 – 1 \right) + 1( – 4 + 1)\]
= 0 + 3 – 3
= 0
Let Cij be the cofactors of the elements aij in A.
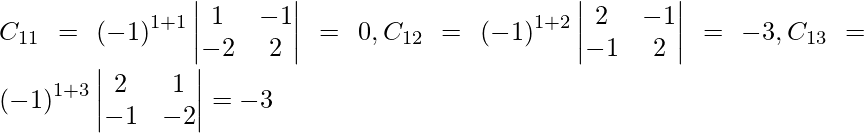
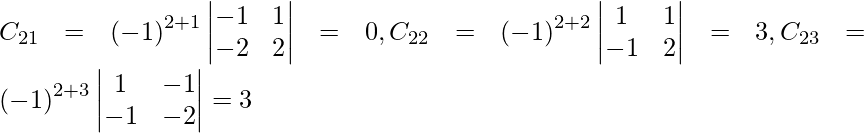
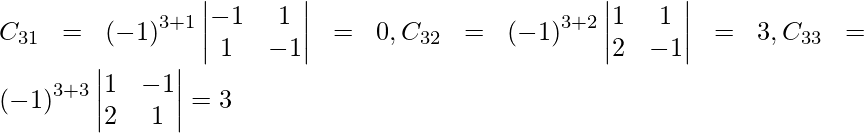

= 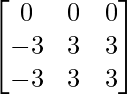
(adj A) B = 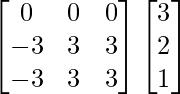
= 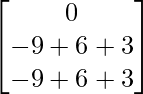
= 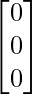
Therefore, the system is consistent and has infinitely many solutions.
Hence proved.
(v) x + y + z = 6
x + 2y + 3z = 14
x + 4y + 7z = 30
Solution:
Here,
x + y + z = 6
x + 2y + 3z = 14
x + 4y + 7z = 30
A = 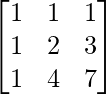 , X =
, X = 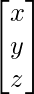 and B =
and B = 
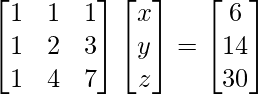
|A| = 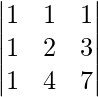
= 2 – 4 + 2
= 0
Let Cij be the cofactors of the elements aij in A.
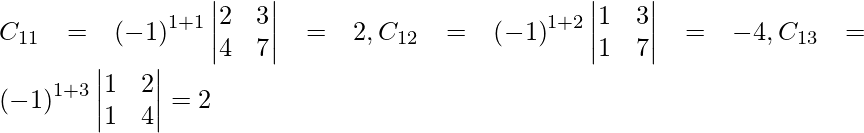
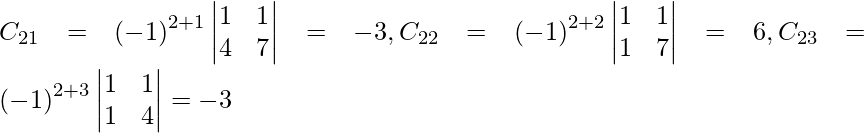
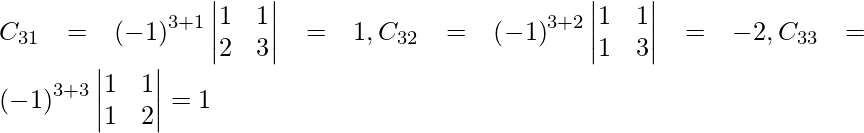
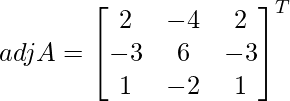
= 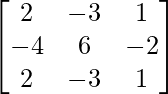
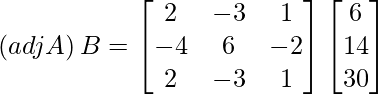
= 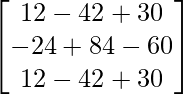
= 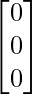
Therefore, the system is consistent and has infinitely many solutions.
Hence proved.
(vi) 2x + 2y − 2z = 1
4x + 4y − z = 2
6x + 6y + 2z = 3
Solution:
Here,
2x + 2y − 2z = 1
4x + 4y − z = 2
6x + 6y + 2z = 3
A = 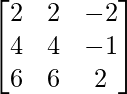 , X =
, X = 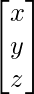 and B =
and B = 
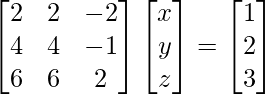
|A| = 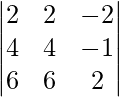
= 2 (8 + 6) – 2 (8 + 6) – 2 (24 – 24)
= 28 – 28 – 0
= 0
Let Cij be the cofactors of the elements aij in A.
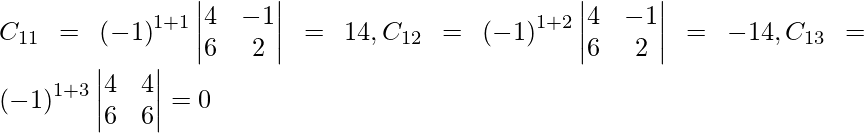
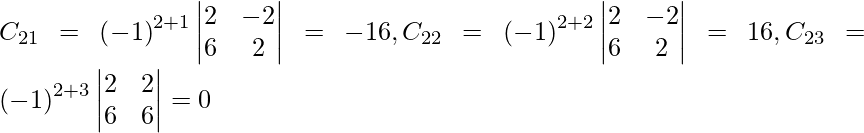
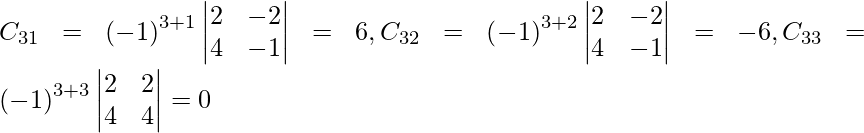
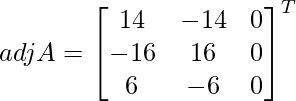
= 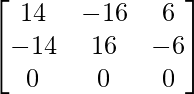
(adj A) B = 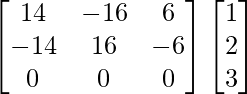
= 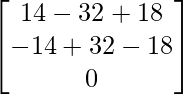
= 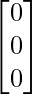
Therefore, the system is consistent and has infinitely many solutions.
Hence proved.
Question 4. Show that each one of the following systems of linear equation is inconsistent:
(i) 2x + 5y = 7
6x + 15y = 13
Solution:
The given system of equations can be expressed as follows:
AX = B
Here,
A = 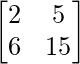 , X =
, X = 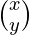 and B =
and B = 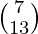
Now,
|A| = 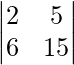
= 30 – 30
= 0
Let Cij be the cofactors of the elements aij in A.
C11 = 15, C12 = -6, C21 = -5 and C22 = 2
adj A = 
= 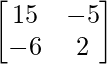
(adj A) B = 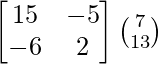
= 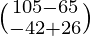
= 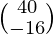 ≠ 0
≠ 0
Therefore, the given system of equations is inconsistent.
Hence proved.
(ii) 2x + 3y = 5
6x + 9y = 10
Solution:
The given system of equations can be expressed as follows:
AX = B
Here,
A = 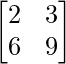 , X =
, X = 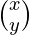 and B =
and B = 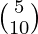
|A| = 
= 18 – 18
= 0
Let Cij be the cofactors of the elements aij in A.
C11 = 9, C12 = -6, C21 = -3 and C22 = 2
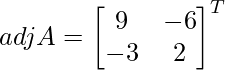
= 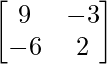
(adj A) B = 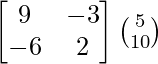
= 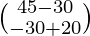
= 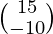 ≠ 0
≠ 0
Therefore, the given system of equations is inconsistent.
Hence proved.
(iii) 4x − 2y = 3
6x − 3y = 5
Solution:
The given system of equations can be expressed as,
AX = B
Here,
A = 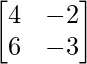 , X =
, X = 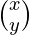 and B =
and B = 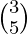
|A| = 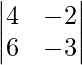
= 12 – 12
= 0
Let Cij be the cofactors of the elements aij in A.
C11 = -3, C12 = -6, C21 = 2 and C22 = 4
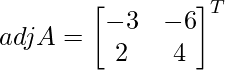
= 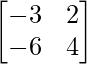
(adj A) B = 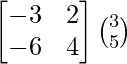
= 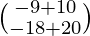
= 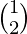 ≠ 0
≠ 0
Therefore, the given system of equations is inconsistent.
Hence proved.
(iv) 4x − 5y − 2z = 2
5x − 4y + 2z = −2
2x + 2y + 8z = −1
Solution:
The given system of equations can be written as,
AX = B
Here,
A = 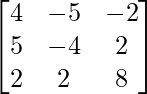 , X =
, X = 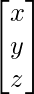 and B =
and B = 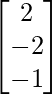
|A| = 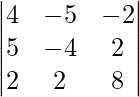
= -144 + 180 – 36
= 0
Let Cij be the cofactors of the elements aij in A.
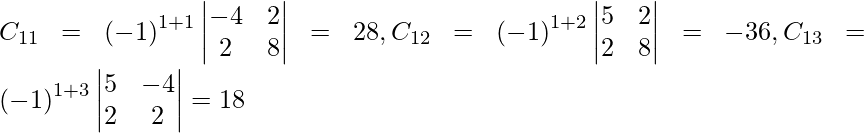
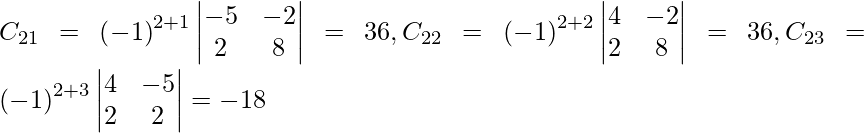
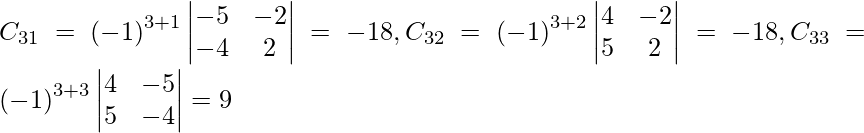
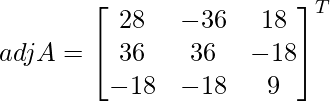
= 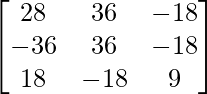
(adj A) B = 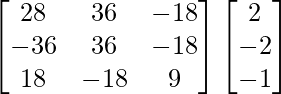
= 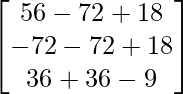
= 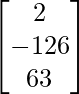 ≠ 0
≠ 0
Therefore, the given system of equations is inconsistent.
Hence proved.
(v) 3x − y − 2z = 2
2y − z = −1
3x − 5y = 3
Solution:
The given system of equations can be written as,
AX = B
Here,
A = 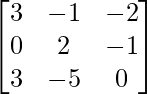 , X =
, X = 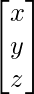 and B =
and B = 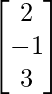
|A| = 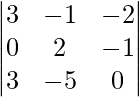
= -15 + 3 + 12
= 0
Let Cij be the cofactors of the elements aij in A.
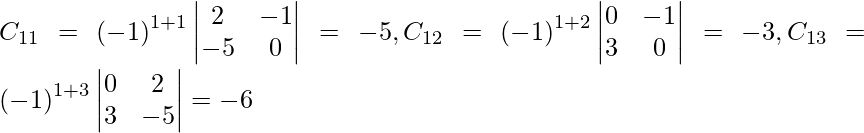
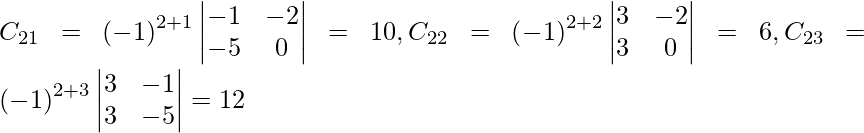
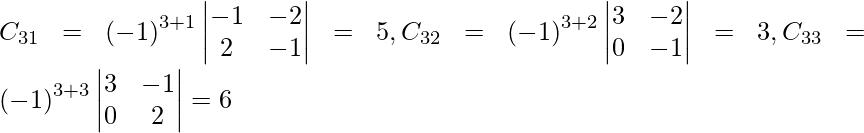
adj A = 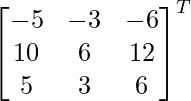
= 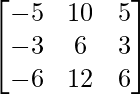
(adj A) B = 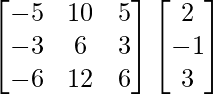
= 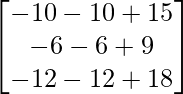
= 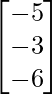 ≠ 0
≠ 0
Therefore, the given system of equations is inconsistent.
Hence proved.
(vi) x + y − 2z = 5
x − 2y + z = −2
−2x + y + z = 4
Solution:
The given system of equations can be written as,
AX = B
Here,
A = 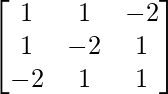 , X =
, X = 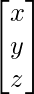 and B =
and B = 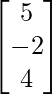
|A| = 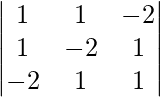
= – 3 – 3 + 6
= 0
Let Cij be the cofactors of the elements aij in A.
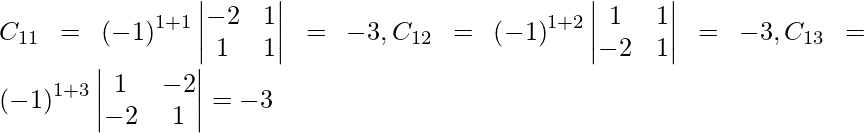
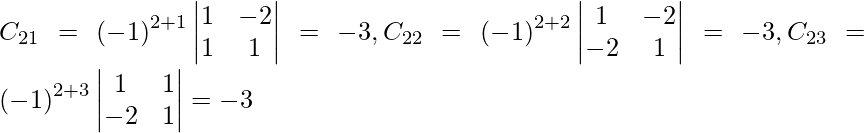
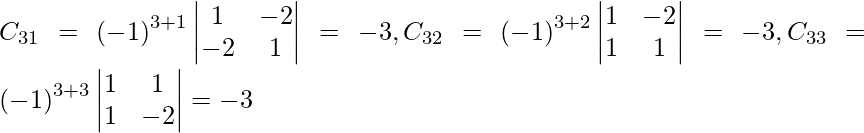
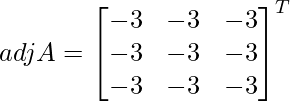
= 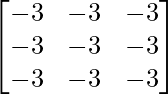
(adj A) B = 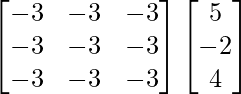
= 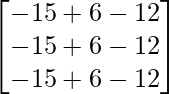
=  ≠ 0
≠ 0
Therefore, the given system of equations is inconsistent.
Hence proved.
Question 5. If A = 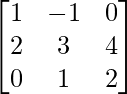 and B =
and B = 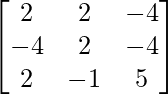 are two square matrices, find AB and hence solve the system of linear equations: x − y = 3, 2x + 3y + 4z = 17, y + 2z = 7.
are two square matrices, find AB and hence solve the system of linear equations: x − y = 3, 2x + 3y + 4z = 17, y + 2z = 7.
Solution:
Here,
A = 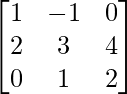 and B =
and B = 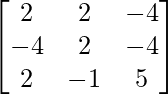
Now,
AB = 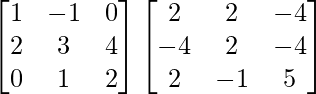
AB = 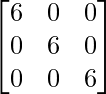
AB = 
AB = 6I
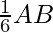 = I
= I
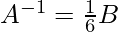
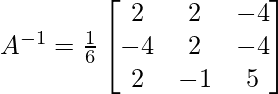
X = A-1 B
X = 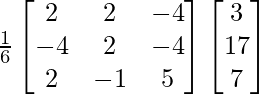
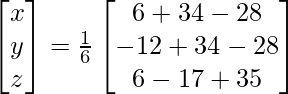
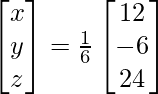
Therefore x = 2, y = -1 and z = 4.
Question 6. If A = 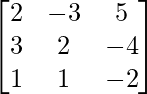 , find A−1 and hence solve the system of linear equations 2x − 3y + 5z = 11, 3x + 2y − 4z = −5, x + y + 2z = −3.
, find A−1 and hence solve the system of linear equations 2x − 3y + 5z = 11, 3x + 2y − 4z = −5, x + y + 2z = −3.
Solution:
Here,
A = 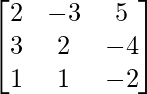
|A| = 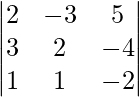
= 0 – 6 + 5
= -1
Let Cij be the cofactors of the elements aij in A.
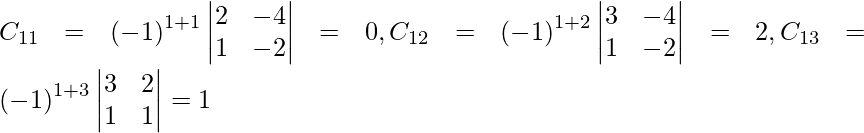
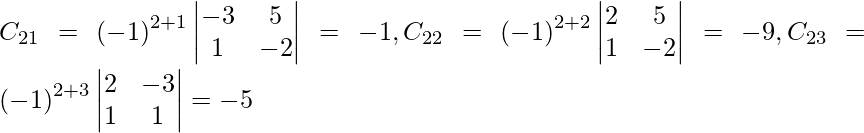
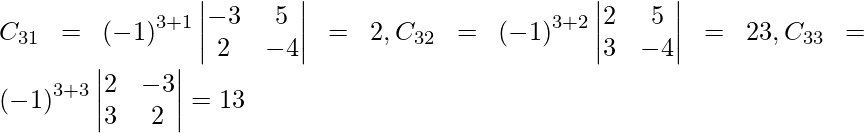
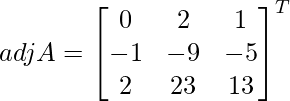
= 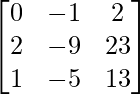
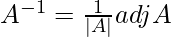
= 
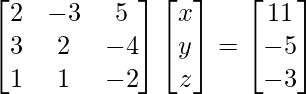
X = A-1 B

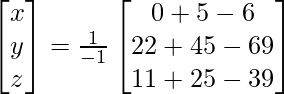
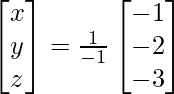
=> x = – 1/- 1, y = -2/-1\ and z = -3/-1
Therefore x = 1, y = 2 and z = 3.
Question 7. Find A−1, if A = 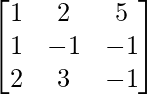 . Hence solve the following system of linear equations: x + 2y + 5z = 10, x − y − z = −2, 2x + 3y − z = −11.
. Hence solve the following system of linear equations: x + 2y + 5z = 10, x − y − z = −2, 2x + 3y − z = −11.
Solution:
A = 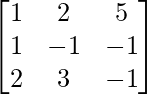
|A| = 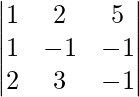
= 4 – 2 + 25
= 27
Let Cij be the cofactors of the elements aij in A.
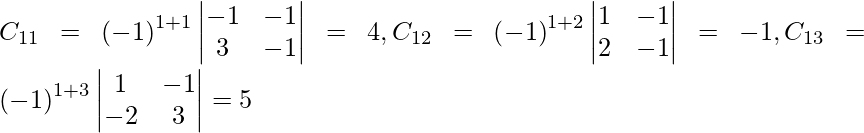
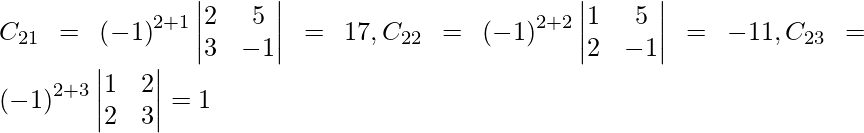
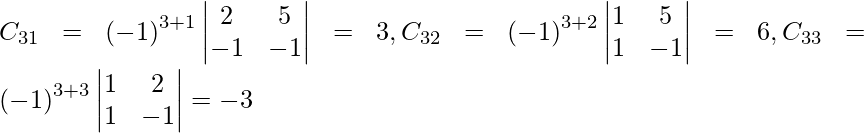
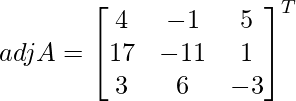
= 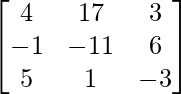
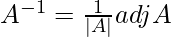
= 
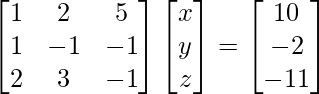
X = A-1 B
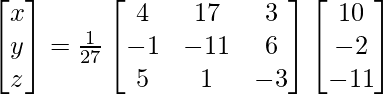
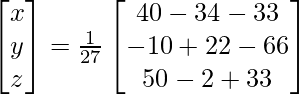
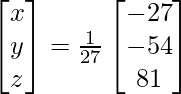
=> x = -27/27, y = -54/27 and z = 81/27
Therefore, x = – 1, y = -2 and z = 3.
Share your thoughts in the comments
Please Login to comment...