Class 12 RD Sharma Solutions – Chapter 31 Probability – Exercise 31.7 | Set 1
Last Updated :
21 Jul, 2021
Question 1. The contents of urns I, II, III are as follows:
Urn I: 1 white, 2 black, and 3 red balls
Urn II: 2 white, 1 black, and 1 red ball
Urn III: 4 white, 5 black, and 3 red balls
One urn is chosen at random and two balls are drawn. They happen to be white and red. What is the probability that they come from Urns I, II, III?
Solution:
Let us assume that E1, E2 and E3 be the events of selecting Urn I, Urn II and Urn III. And also A be the event that the two balls drawn are white and red.
So, P(E1) = 1/3
P(E2) = 1/3
P(E3) = 1/3
Now,
P(A/E1) = 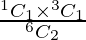 = 3/15 = 1/5
= 3/15 = 1/5
P(A/E2) = 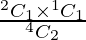 = 2/6 = 1/3
= 2/6 = 1/3
P(A/E3) = 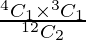 = 12/66 = 2/11
= 12/66 = 2/11
By using Bayes’ theorem, the required probability is,
P(E1/A) = 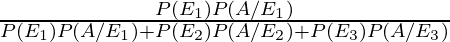
= 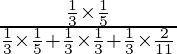
= 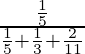
= 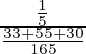
= 33/118
P(E2/A) = 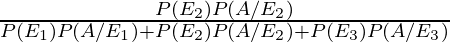
= 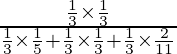
= 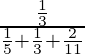
= 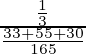
= 55/118
P(E3/A) = 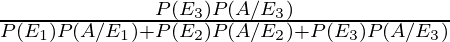
= 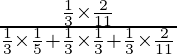
= 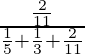
= 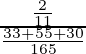
= 30/118
Question 2. A bag A contains 2 white and 3 red balls and a bag B contains 4 white and 5 red balls. One ball is drawn at random from one of the bags and is found to be red. Find the probability that it was drawn from bag B.
Solution:
Let us assume that the A, E1 and E2 be the events that the ball is red, bag A is chosen and bag B is chosen.
So, P(E1) = 1/2
P(E2) = 1/2
Now,
P(A/E1) = 3/5
P(A/E2) = 5/9
By using Bayes’ theorem, the required probability is,
P(E2/A) = 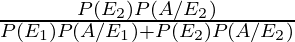
= 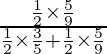
= 25/52
Question 3. Three urns contain 2 white and 3 black balls; 3 white and 2 black balls and 4 white and 1 black ball respectively. One ball is drawn from an urn chosen at random and it was found to be white. Find the probability that it was drawn from the first urn.
Solution:
Let us consider E1, E2 and E3 be the events of selecting Urn I, Urn II and Urn III.
Also, A be the event that the ball drawn is white.
So, P(E1) = 1/3
P(E2) = 1/3
P(E3) = 1/3
Now,
P(A/E1) = 2/5
P(A/E2) = 3/5
P(A/E3) = 4/5
By using Bayes’ theorem, the required probability is,
P(E1/A) = 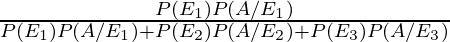
= 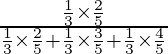
= 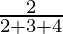
= 2/9
Question 4. The contents of the three urns are as follows:
Urn 1: 7 white, 3 black balls, Urn 2: 4 white, 6 black balls, and Urn 3: 2 white, 8 black balls. One of these urns is chosen at random with probabilities 0.20, 0.60, and 0.20 respectively. From the chosen urn two balls are drawn at random without replacement. If both these balls are white, what is the probability that these came from urn 3?
Solution:
Let us assume that E1, E2 and E3 be the events of selecting Urn I, Urn II and Urn III. Also, A be the event that the two balls drawn are white.
So, P(E1) = 20/100
P(E2) = 60/100
P(E3) = 20/100
Now,
P(A/E1) = 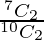 = 21/45
= 21/45
P(A/E2) = 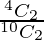 = 6/45
= 6/45
P(A/E3) = 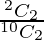 = 1/45
= 1/45
By using Bayes’ theorem, the required probability is,
P(E3/A) = 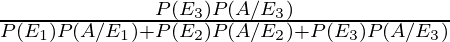
= 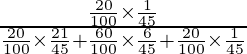
= 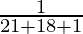
= 1/40
Question 5. Suppose a girl throws a die. If she gets 1 or 2, she tosses a coin three times and notes the number of tails. If she gets 3, 4, 5, or 6, she tosses a coin once and notes whether a ‘head’ or ‘tail’ is obtained. If she obtained exactly one ‘tail’, then what is the probability that she threw 3, 4, 5, or 6 with the die?
Solution:
Let us consider E1 be the event that the outcome on the die is 1 or 2 and E2 be the event that outcome on the die is 3, 4, 5 or 6.
Now, P(E1) = 2/6 = 1/3 and P(E2) = 4/6 = 2/3
Also, let us assume A be the event of getting exactly one ‘tail’.
So, P(A/E1) = 3/8
P(A/E2) = 1/2
Now, P(E2/A) is the probability that the girl threw 3, 4, 5 or 6 with the die, if she obtained exactly one tail
So, by using Bayes’ theorem, the required probability is,
P(E2/A) = 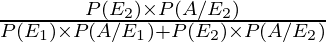
= 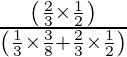
= 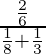
= 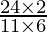
= 8/11
Question 6. Two groups are competing for the positions of the Board of Directors of a Corporation. The probabilities that the first and the second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product introduced was by the second group.
Solution:
Let us consider E1 and E2 be the events that the first group and the second group win the competition. Also, A be the event of introducing a new product.
So, P(E1) = 0.6
P(E2) = 0.4
P(A/E1) = 0.7
P(A/E2) = 0.3
Now, P(E2/A) is the probability that the new product is introduced by the second group
So, by using Bayes’ theorem, the required probability is,
P(E2/A) = 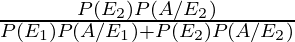
= 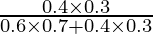
= 0.12/0.54
= 2/9
Question 7. Suppose 5 men out of 100 and 25 women out of 1000 are good orators. An orator is chosen at random. Find the probability that a male person is selected. Assume that there are equal numbers of men and women.
Solution:
Let us assume that A, E1 and E2 be the events that the person is a good orator, is a man and is a woman.
So, P(E1) = 1/2
P(E2) = 1/2
Now,
P(A/E1) = 5/100
P(A/E2) = 25/1000
So, using Bayes’ theorem, the required probability is,
P(E1/A) = 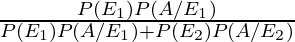
= 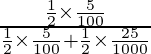
= 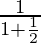
= 2/3
Question 8. A letter is known to have come either from LONDON or CLIFTON. On the envelope just two consecutive letters ON are visible. What is the probability that the letter has come from
(i) LONDON (ii) CLIFTON?
Solution:
Let us consider A, E1 and E2 be the events that the two consecutive letters are visible and the letter has come from LONDON and CLIFTON.
So, P(E1) = 1/2
P(E2) = 1/2
Now,
P(A/E1) = 2/5
P(A/E2) = 1/6
So, using Bayes’ theorem, the required probability is,
(i) P(E1/A) = 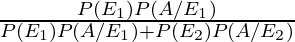
= 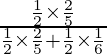
= 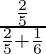
= 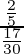
= 12/17
(ii) P(E2/A) = 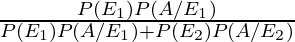
= 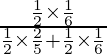
= 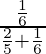
= 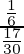
= 5/17
Question 9. In a class, 5% of the boys and 10% of the girls have an IQ of more than 150. In this class, 60% of the students are boys. If a student is selected at random and found to have an IQ of more than 150, find the probability that the student is a boy.
Solution:
Let us consider A, E1 and E2 be the events that the IQ is more than 150, the selected student is a boy and the selected student is a girl.
So, P(E1) = 60/100
P(E2) = 40/100
Now,
P(A/E1) = 5/100
P(A/E2) = 10/100
So, using Bayes’ theorem, the required probability is,
P(E1/A) = 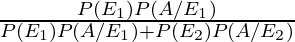
= 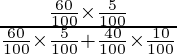
= 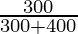
= 300/700
= 3/7
Question 10. A factory has three machines, X, Y, and Z producing 1000, 2000, and 3000 bolts per day respectively. The machine X produces 1% defective bolts, Y produces 1.5% and Z produces 2% defective bolts. At the end of the day, a bolt is drawn at random and is found to be defective. What is the probability that this defective bolt has been produced by machine X?
Solution:
Let us assume that E1, E2 and E3 be the events that machine X produces bolts, machine Y produces bolts and machine Z produces bolts. Also, A be the event that the bolt is defective.
So, the total number of bolts = 1000 + 2000 + 3000 = 6000
P(E1) = 1000/6000 = 1/6
P(E2) = 2000/6000 = 1/3
P(E3) = 3000/6000 = 1/2
Now, P(E1/A) is the probability that the defective bolt is produced by machine X
So,
P(A/E1) = 1% = 1/100
P(A/E2) = 1.5% = 15/1000
P(A/E3) = 2% = 2/100
So, using Bayes’ theorem, the required probability is,
P(E1/A) = 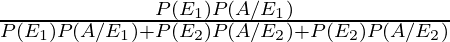
= 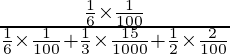
= 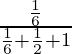
= 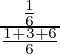
= 1/10
Question 11. An insurance company insured 3000 scooters, 4000 cars, and 5000 trucks. The probabilities of the accident involving a scooter, a car, and a truck are 0.02, 0.03, and 0.04 respectively. One of the insured vehicles meets with an accident. Find the probability that it is an (i) scooter (ii) car (iii) truck.
Solution:
Let us assume that E1, E2 and E3 be the events that the vehicle is a scooter, a car and a truck. Also, A be the event that the vehicle meets with an accident.
From the question, insurance company insured 3000 scooters, 4000 cars and 5000 trucks.
So, the total number of vehicles = 3000 + 4000 + 5000 = 12000
P(E1) = 3000/12000 = 1/4
P(E2) = 4000/12000 = 1/3
P(E3) = 5000/12000 = 5/12
Now, P(E1/A) is the probability that the vehicle, which meets with an accident, is a scooter
Now,
P(A/E1) = 0.02 = 2/100
P(A/E2) = 0.03 = 3/100
P(A/E3) = 0.04 = 4/100
So, using Bayes’ theorem, the required probability is,
(i) P(E1/A) = 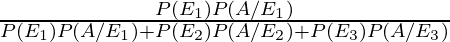
= 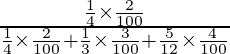
= 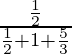
= 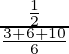
= 3/19
(ii) P(E2/A) = 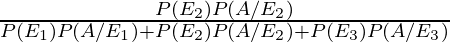
= 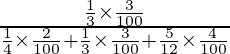
= 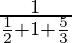
= 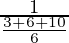
= 6/19
(iii) P(E3/A) = 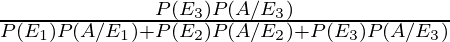
= 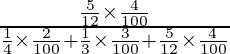
= 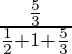
= 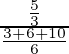
= 10/19
Question 12. Suppose we have four boxes A, B, C, D containing colored marbles as given below:
Box
| Colour
|
| Red
| White
| Black
|
A
| 1
| 6
| 3
|
B
| 6
| 2
| 2
|
C
| 8
| 1
| 1
|
D
| 0
| 6
| 4
|
One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box A, box B, and box C?
Solution:
Let us assume that R be the event of drawing the red marble and EA, EB and EC be the events of selecting box A, box B and box C.
According to the question, the total number of marbles are 40 and the number of red marbles are 15.
So, P(R) = 15/40 = 3/8
P(EA/R) = The probability of drawing a red marble from box A.
P(EA/R) = 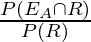
= 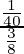
= 1/15
P(EB/R) = The probability of drawing a red marble from box B.
P(EB/R \right) = 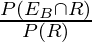
= 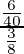
= 2/5
P(EC/R) = The probability of drawing a red marble from box C.
P(EC/R) = 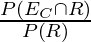
= 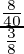
= 8/15
Question 13. A manufacturer has three machine operators, A, B, and C. The first operator, A produces 1% defective items, whereas the other two operators, B and C produce 5% and 7% defective items respectively. A is on the job for 50% of the time, B on the job for 30% of the time, and C on the job for 20% of the time. A defective item is produced. What is the probability that it was produced by A?
Solution:
Let us consider E1, E2 and E3 be the time taken by machine operators A, B, and C. Also, X be the event of producing defective items.
P(E1) = 50 % = 1/2
P(E2) = 30 % = 3/10
P(E3) = 20 % = 1/5
Now,
P(X/E1) = 1 % = 1/100
P(X/E2) = 5 % = 5/100
P(X/E3) = 7 % = 7/100
So, using Bayes’ theorem, the required probability is,
P(E1/X) = 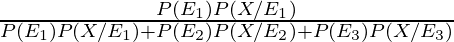
= 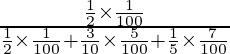
= 5/34
Share your thoughts in the comments
Please Login to comment...