Class 12 RD Sharma Solutions – Chapter 23 Algebra of Vectors – Exercise 23.6 | Set 1
Last Updated :
28 Mar, 2021
Question 1: Find the magnitude of the vector 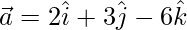 .
.
Solution:
Magnitude of a vector 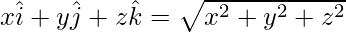
=>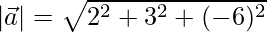
=> 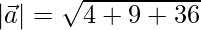
=> 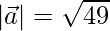
=>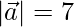
Question 2: Find the unit vector in the direction of 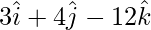 .
.
Solution:
We know that unit vector of a vector  is given by,
is given by,
=> 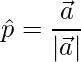
=> 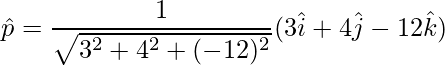
=> 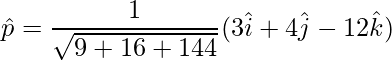
=> 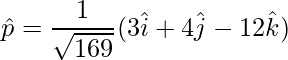
=> 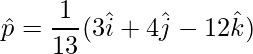
Question 3: Find a unit vector in the direction of the resultant of the vectors 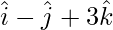 ,
, 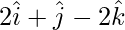 and
and 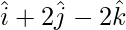 .
.
Solution:
Let,
=>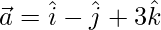
=> 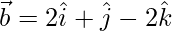
=> 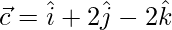
Let 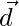 be the resultant,
be the resultant,
=> 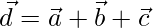
=> 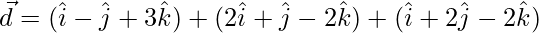
=> 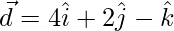
Unit vector is,
=> 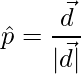
=> 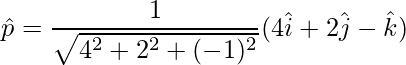
=> 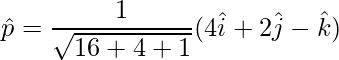
=> 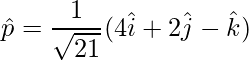
Question 4: The adjacent sides of a parallelogram are represented by the vectors 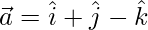 and
and 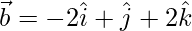 . Find the unit vectors parallel to the diagonals of the parallelogram.
. Find the unit vectors parallel to the diagonals of the parallelogram.
Solution:
Let PQRS be the parallelogram.
Given that, PQ = 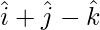 and QR =
and QR = 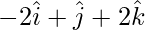 .
.
Thus, the diagonals are: PR and SQ.
=> 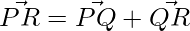
=> 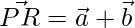
=> 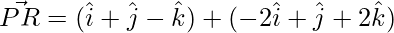
=> 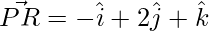
=> 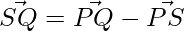
=> 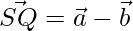
=> 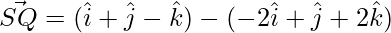
=> 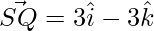
Thus the unit vectors in the direction of the diagonals are:
=> 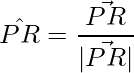
=> 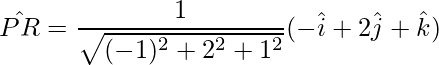
=> 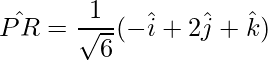
=> 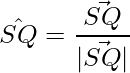
=> 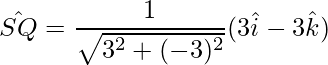
=> 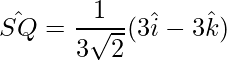
Question 5: If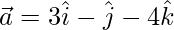 ,
, 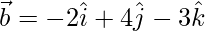 and
and 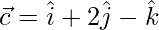 , find
, find 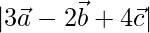 .
.
Solution:
Given, 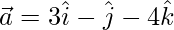 ,
, 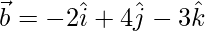 and
and 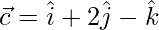 .
.
Let,
=> 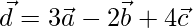
=> 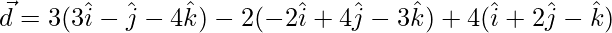
=> 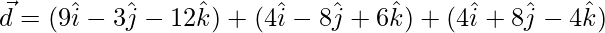
=> 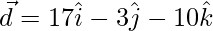
The magnitude is given by,
=> 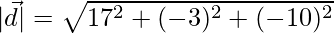
=> 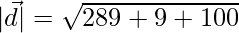
=>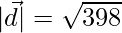
Question 6: If 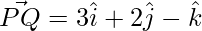 and the coordinates of P are (1,-1,2), find the coordinates of Q.
and the coordinates of P are (1,-1,2), find the coordinates of Q.
Solution:
Given, 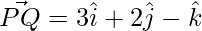
And, 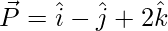
=> 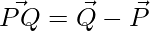
=>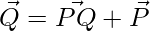
=> 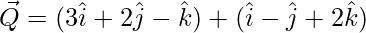
=> 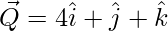
=> Thus the coordinates of Q are (4,1,1).
Question 7: Prove that the points 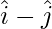 ,
, 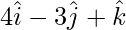 and
and 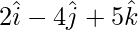 are the vertices of a right-angled triangle.
are the vertices of a right-angled triangle.
Solution:
Let,
=>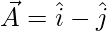
=> 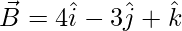
=> 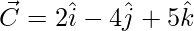
Thus, the 3 sides of the triangle are,
=> 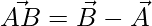
=> 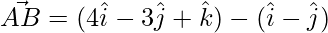
=> 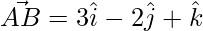
=> 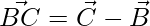
=> 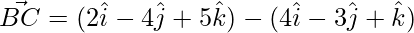
=> 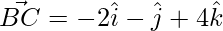
=> 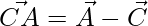
=> 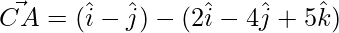
=> 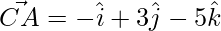
The lengths of every side are given by their magnitude,
=> 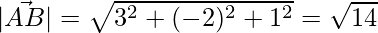
=>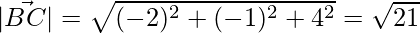
=>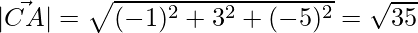
As we can see,
=>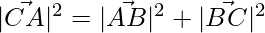
=> These 3 points form a right-angled triangle.
Question 8: If the vertices A, B and C of a triangle ABC are the points with position vectors 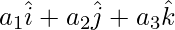 ,
, 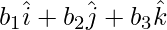 ,
, 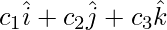 respectively, what are the vectors determined by its sides? Find the length of these vectors.
respectively, what are the vectors determined by its sides? Find the length of these vectors.
Solution:
Let,
=> 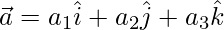
=> 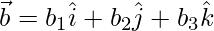
=> 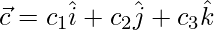
The sides of the triangle are given as,
=> 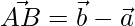
=> 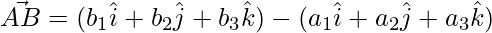
=> 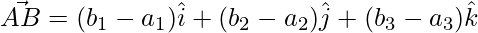
=> 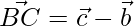
=> 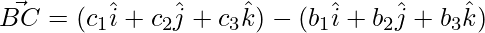
=> 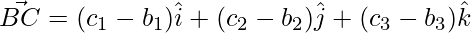
=> 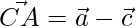
=> 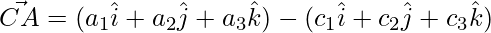
=> 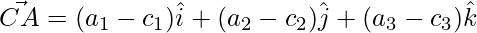
The lengths of the sides are,
=>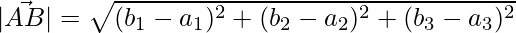
=> 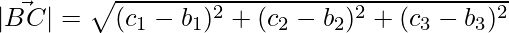
=> 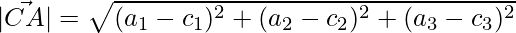
Question 9: Find the vector from the origin O to the centroid of the triangle whose vertices are (1,-1,2), (2,1,3), and (-1,2,-1).
Solution:
The position of the centroid is given by,
=> (x, y, z) = 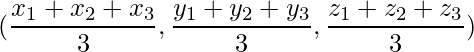
=> (x, y, z) = 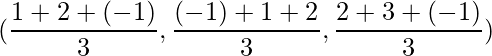
=> (x, y, z) = 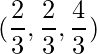
The vector to the centroid from O is,
=> 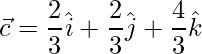
Question 10: Find the position vector of a point R which divides the line segment joining points p(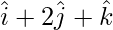 ) and q(
) and q(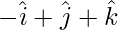 ) in the ratio 2:1.
) in the ratio 2:1.
(i) Internally
Solution:
The position vectors of a point that divides a line segment internally are given by,
=> 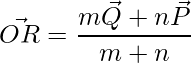 , where
, where 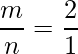
=>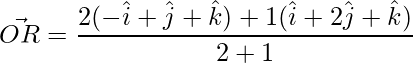
=> 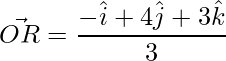
(ii) Externally
Solution:
The position vectors of a point that divides a line segment externally are given by,
=> 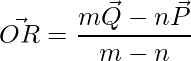 , where
, where 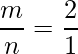
=> 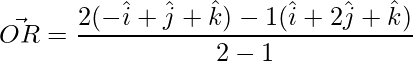
=> 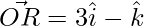
Share your thoughts in the comments
Please Login to comment...