Class 12 RD Sharma Solutions- Chapter 29 The Plane – Exercise 29.7
Last Updated :
25 Jan, 2021
Question 1. Find the vector equation of the following planes in scalar product form 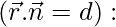
Solution:
(i) 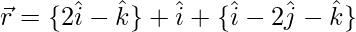
Here, 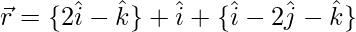
We know that, 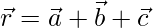 represent a plane passing through a point having position vector
represent a plane passing through a point having position vector  and parallel to vectors
and parallel to vectors 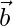 and .
and .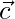
Here, 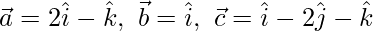
The given plane is perpendicular to a vector
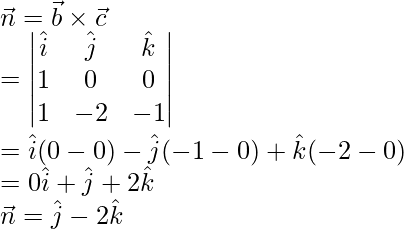
We know that vector equation of plane in scalar product form is,
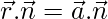 —(Equation-1)
—(Equation-1)
Put 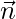 and
and  in (Equation-1),
in (Equation-1),
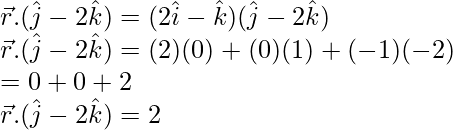
The equation is required form is,
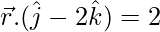
(ii) 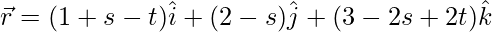
Here,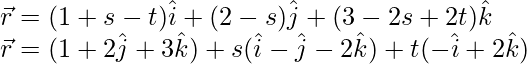
We know that, 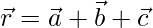 represent a plane passing through a point having position vector
represent a plane passing through a point having position vector  and parallel to vectors
and parallel to vectors 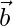 and
and 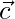
Here, 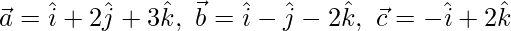
The given plane is perpendicular to a vector
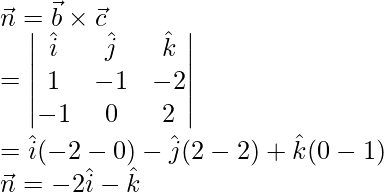
We know that, vector equation of a plane is scalar product is,
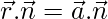 —(Equation-1)
—(Equation-1)
Put value of  and
and 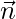 in (Equation-1)
in (Equation-1)

Multiplying both the sides by (-1),
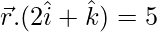
The equation in the required form,
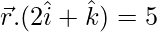
(iii) 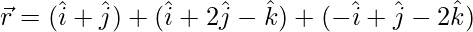
Given, equation of plane,
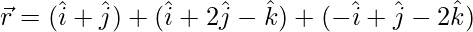
We know that, 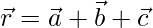 is the equation of a plane passing through point
is the equation of a plane passing through point  and parallel to
and parallel to 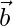 and
and 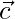 .
.
Here, 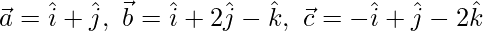
The given plane is perpendicular to a vector
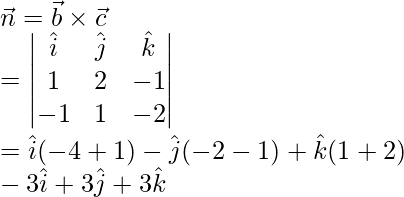
We know that, equation of plane in scalar product form is given by,

Dividing by 3, we get
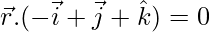
Equation in required form is,
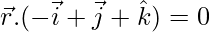
(iv) 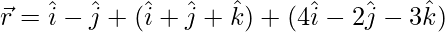
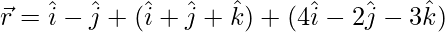
Plane is passing through 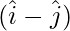 and parallel to b
and parallel to b 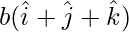 and
and 
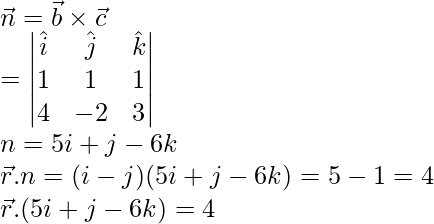
Question 2. Find the cartesian form of the equation of the following planes:
Solution:
(i) 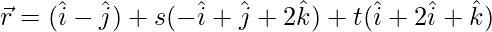
Here, given equation of plane is,
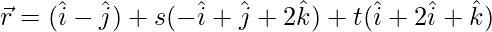
We know that, 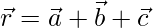 represents the equation of a plane passing through a vector
represents the equation of a plane passing through a vector  and parallel to vector
and parallel to vector 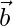 and
and 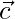 .
.
Here, 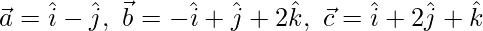
Given plane is perpendicular to vector
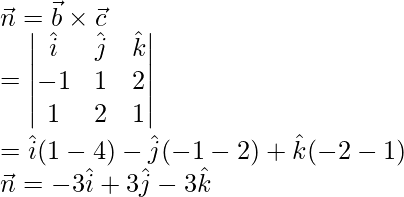
We know that, equation of plane in the scalar product form,
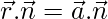 —Equation-1
—Equation-1
Put the value of  and
and 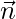 in Equation-1,
in Equation-1,
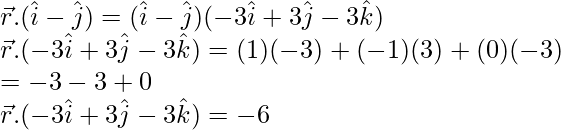
Put 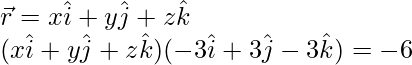
(x)(-3) + (y)(3) + (z)(-3) = -6
-3x + 3y – 3z = -6
Dividing by (-3), we get
x – y + z = 2
Equation in required form is,
x – y + z = 2
(ii) 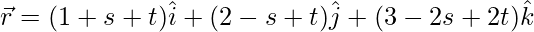
Given, equation of plane,

We know that, 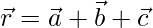 represents the equation of a plane passing through the vector
represents the equation of a plane passing through the vector  and parallel to vector
and parallel to vector 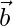 and
and 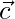
Here, 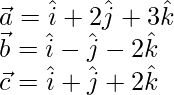
The given plane is perpendicular to vector
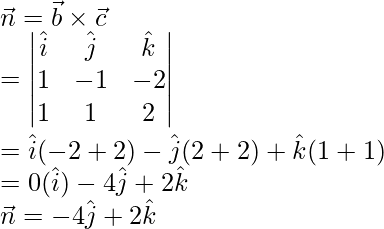
We know that, equation of plane in scalar product form is given by,
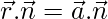 —Equation-1
—Equation-1
Put, the value of  and
and 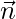 in equation-1
in equation-1
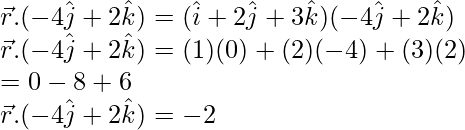
Put 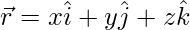
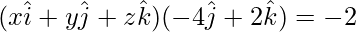
(x)(0) + (y)(-4) + (z)(2) = -2
-4y + 2z = -2
The equation in required form is,
2y – z = 1
Question 3. Find the vector equation of the following planes in non-parametric form:
Solution:
(i) 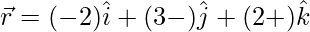
Given, equation of plane is,
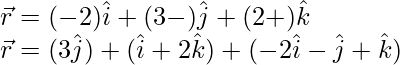
We know that, 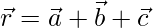 represents the equation of a plane passing through a point
represents the equation of a plane passing through a point  and parallel to vector
and parallel to vector 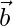 and
and 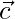 .
.
Given,
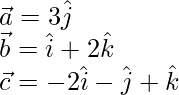
The given plane is perpendicular to
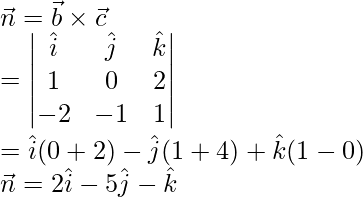
Vector equation of plane in non-parametric form is.
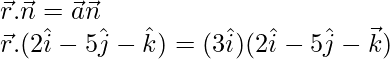
= (0)(2) + (3)(-5) + (0)(-1)
= 0 – 15 + 0
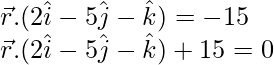
The required form of equation is,
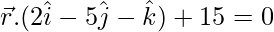
(ii) 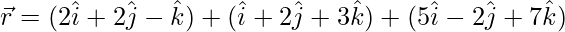
Given, equation of plane is,
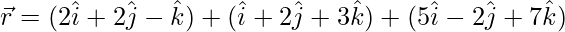
We know that, 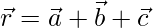 represents the equation of a plane passing through a vector
represents the equation of a plane passing through a vector  and parallel to vector
and parallel to vector 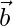 and
and 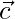 .
.
Here,
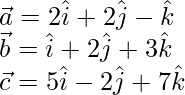
The given plane is perpendicular to vector
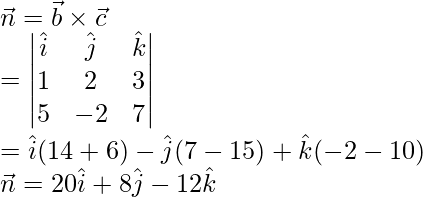
We know that, equation of a plane in non-parametric form is given by,
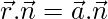
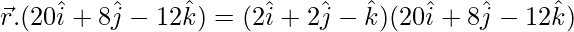
= (2)(20) + (2)(8) – (-1)(-12)
=40 + 16 + 12
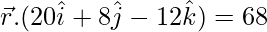
Dividing by 4,
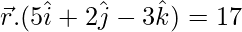
Equation of plane in required form is,
Share your thoughts in the comments
Please Login to comment...