Evaluate the following definite integrals:
Question 42. 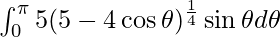
Solution:
We have,
I = 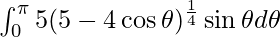
Let 5 – 4 cos θ = t. So, we have
=> 4 sin θ dθ = dt
=> sin θ dθ = dt/4
Now, the lower limit is, θ = 0
=> t = 5 – 4 cos θ
=> t = 5 – 4 cos 0
=> t = 5 – 4
=> t = 1
Also, the upper limit is, θ = π
=> t = 5 – 4 cos θ
=> t = 5 – 4 cos π
=> t = 5 + 4
=> t = 9
So, the equation becomes,
I = 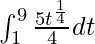
I = 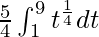
I = ![Rendered by QuickLaTeX.com \frac{5}{4}\left[\frac{t^{\frac{5}{4}}}{\frac{5}{4}}\right]_{1}^{9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f1e5b2ca2e3ed3842d648126b276a3ba_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{5}{4}\left[\frac{4}{5}t^{\frac{5}{4}}\right]_{1}^{9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-507a704c3a9f061b6d718a6e47a24862_l3.png)
I = ![Rendered by QuickLaTeX.com \left[t^{\frac{5}{4}}\right]_{1}^{9}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f1bc859be7d7153da05889b7109443fb_l3.png)
I = 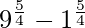
I = 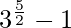
I = 9√3 – 1
Therefore, the value of 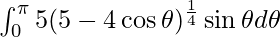 is 9√3 – 1.
is 9√3 – 1.
Question 43. 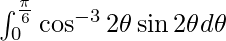
Solution:
We have,
I = 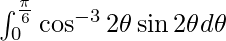
I = 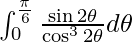
I = 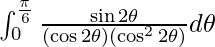
I = 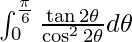
I = 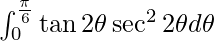
Let tan 2θ = t. So, we have
=> 2 sec2 2θ dθ = dt
=> sec2 2θ dθ = dt/2
Now, the lower limit is, θ = 0
=> t = tan 2θ
=> t = tan 0
=> t = 0
Also, the upper limit is, θ = π/6
=> t = tan 2θ
=> t = tan π/3
=> t = √3
So, the equation becomes,
I = 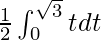
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{t^2}{2}\right]_{0}^{\sqrt{3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d99afdc30e9eb343d69b4d8e93fa666e_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{3}{2}-0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-704047daa35867e954cee933155e799d_l3.png)
I = 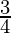
Therefore, the value of 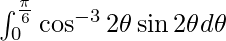 is
is 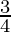 .
.
Question 44. 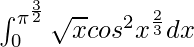
Solution:
We have,
I = 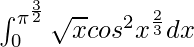
Let 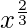 = t. So, we have
= t. So, we have
=> 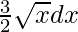 = dt
= dt
Now, the lower limit is, x = 0
=> t = 
=> t = 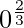
=> t = 0
Also, the upper limit is, x = 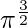
=> t = 
=> t = 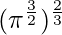
=> t = π
So, the equation becomes,
I = 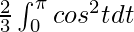
I = 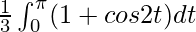
I = ![Rendered by QuickLaTeX.com \frac{1}{3}\left[t+\frac{sin2t}{t}\right]_{0}^{\pi}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-92072596c89929d317ed57dd4c93dae0_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{3}\left[\pi+0-0-0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7a3f05404cfd36db0995cc0b1a0ca22d_l3.png)
I = 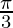
Therefore, the value of 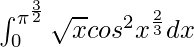 is
is 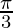 .
.
Question 45. 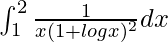
Solution:
We have,
I = 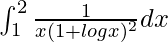
Let 1 + log x = t. So, we have
=> 1/x dx = dt
Now, the lower limit is, x = 0
=> t = 1 + log x
=> t = 1 + log 0
=> t = 1
Also, the upper limit is, x = 2
=> t = 1 + log x
=> t = 1 + log 2
So, the equation becomes,
I = 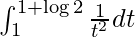
I = ![Rendered by QuickLaTeX.com \left[\frac{-1}{t}\right]_{1}^{1+\log2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4195ffef79fdd3e1d44ac1047909c19b_l3.png)
I = 
I = 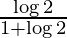
Therefore, the value of 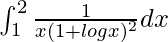 is
is 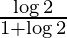 .
.
Question 46. 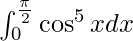
Solution:
We have,
I = 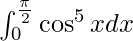
I = 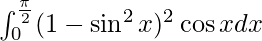
Let sin x = t. So, we have
=> cos x dx = dt
Now, the lower limit is, x = 0
=> t = sin x
=> t = sin 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = sin x
=> t = sin π/2
=> t = 1
So, the equation becomes,
I = 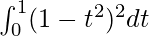
I = 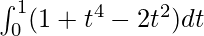
I = ![Rendered by QuickLaTeX.com \left[t-\frac{2}{3}t^3+\frac{t^5}{5}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-327e09d5dbc4fcf6e2ef31a9f2c6bbef_l3.png)
I = 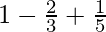
I = 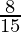
Therefore, the value of 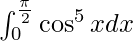 is
is 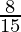 .
.
Question 47. 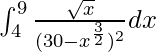
Solution:
We have,
I = 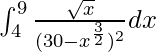
Let 30 – x3/2 = t. So, we have
=> 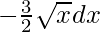 = dt
= dt
=> 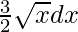 = – dt
= – dt
Now, the lower limit is, x = 4
=> t = 30 – x3/2
=> t = 30 – 43/2
=> t = 30 – 8
=> t = 22
Also, the upper limit is, x = 9
=> t = 30 – x3/2
=> t = 30 – 93/2
=> t = 30 – 27
=> t = 3
So, the equation becomes,
I = 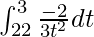
I = 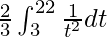
I = ![Rendered by QuickLaTeX.com \frac{2}{3}\left[\frac{-1}{t}\right]_{3}^{22}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a8fc9913fa9374f6763d9e9f093a3d39_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{2}{3}\left[\frac{-1}{22}+\frac{1}{3}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-088e87cd805fbe73119577312da8181b_l3.png)
I = 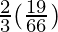
I = 
Therefore, the value of 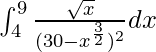 is
is 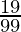 .
.
Question 48. 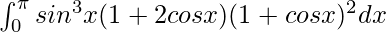
Solution:
We have,
I = 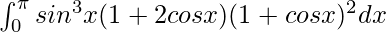
Let cos x = t. So, we have
=> – sin x dx = dt
=> sin x dx = –dt
Now, the lower limit is, x = 0
=> t = cos x
=> t = cos 0
=> t = 1
Also, the upper limit is, x = π
=> t = cos x
=> t = cos π
=> t = –1
So, the equation becomes,
I = 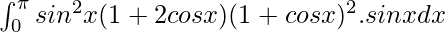
I = 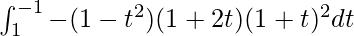
I = 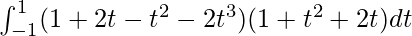
I = 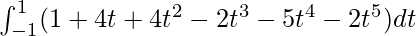
I = ![Rendered by QuickLaTeX.com \left[t+2t^2+\frac{4}{3}t^3-\frac{1}{2}t^4-t^5-\frac{1}{3}t^6\right]_{-1}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d88e87345612c54662316f5367844f37_l3.png)
I = 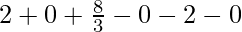
I = 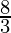
Therefore, the value of 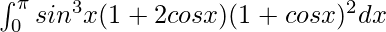 is
is 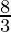 .
.
Question 49. 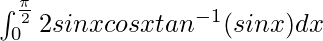
Solution:
We have,
I = 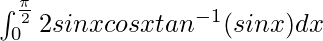
Let sin x = t. So, we have
=> cos x dx = dt
Now, the lower limit is, x = 0
=> t = sin x
=> t = sin 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = sin x
=> t = sin π/2
=> t = 1
So, the equation becomes,
I = 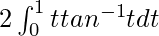
I = ![Rendered by QuickLaTeX.com 2\left[\frac{1}{2}t^2tan^{-1}t-\frac{t}{2}+\frac{1}{2}tan^{-1}t\right]_0^1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-608b0ce112fe1a0ce1647a506a0e03ea_l3.png)
I = 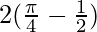
I = 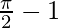
Therefore, the value of 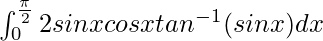 is
is 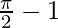 .
.
Question 50. 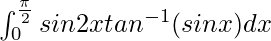
Solution:
We have,
I = 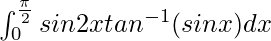
I = 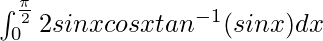
Let sin x = t. So, we have
=> cos x dx = dt
Now, the lower limit is, x = 0
=> t = sin x
=> t = sin 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = sin x
=> t = sin π/2
=> t = 1
So, the equation becomes,
I = 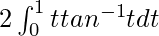
I = ![Rendered by QuickLaTeX.com 2\left[\frac{1}{2}t^2tan^{-1}t-\frac{t}{2}+\frac{1}{2}tan^{-1}t\right]_0^1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-608b0ce112fe1a0ce1647a506a0e03ea_l3.png)
I = 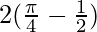
I = 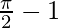
Therefore, the value of 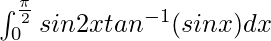 is
is 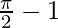 .
.
Question 51. 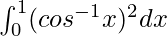
Solution:
We have,
I = 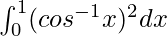
On using integration by parts, we get,
I = 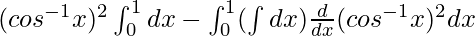
I = ![Rendered by QuickLaTeX.com \left[x(cos^{-1}x)^2\right]_{0}^{1}+2\int_0^1\frac{xcos^{-1}x}{\sqrt{1-x^2}}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ceb12c158faf557754a4d9bb177aaf69_l3.png)
Let cos-1 x = t. So, we have
=> 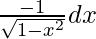 = dt
= dt
Now, the lower limit is, x = 0
=> t = cos-1 x
=> t = cos-1 0
=> t = π/2
Also, the upper limit is, x = 1
=> t = cos-1 x
=> t = cos-1 1
=> t = 0
So, the equation becomes,
I = ![Rendered by QuickLaTeX.com \left[x(cos^{-1}x)^2\right]_{0}^{1}+2\int_\frac{\pi}{2}^0-tcostdt](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54e33845eaa969c002ef8aede754c8f1_l3.png)
I = 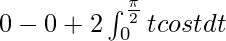
I = 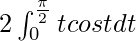
I = 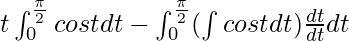
I = ![Rendered by QuickLaTeX.com 2\left[tsint-\int sintdt\right]^\frac{\pi}{2}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b67b8c6727ee1720989bb0d9a44dedd6_l3.png)
I = ![Rendered by QuickLaTeX.com 2\left[tsint+cost\right]^\frac{\pi}{2}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac6fe410e5faf775e26b90bd91d89725_l3.png)
I = 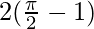
I = π – 2
Therefore, the value of 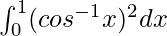 is π – 2.
is π – 2.
Question 52. 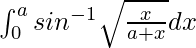
Solution:
We have,
I = 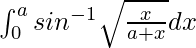
Let x = a tan2 t. So, we have
=> dx = 2a tan t sec2 t dt
Now, the lower limit is, x = 0
=> a tan2 t = x
=> a tan2 t = 0
=> tan t = 0
=> t = 0
Also, the upper limit is, x = a
=> a tan2 t = x
=> a tan2 t = a
=> tan2 t = 1
=> tan t = 1
=> t = π/4
So, the equation becomes,
I = 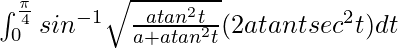
I = 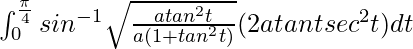
I = 
I = 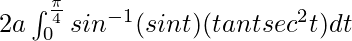
I = 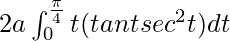
I = ![Rendered by QuickLaTeX.com 2a\left[\frac{ttan^2t}{2}-\int \frac{tan^2t}{2}dt\right]_0^\frac{\pi}{4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c3060df4cbecab428056a535e43cbdd9_l3.png)
I = ![Rendered by QuickLaTeX.com \left[attan^2t-\frac{2a}{2}\int (sec^2t-1)dt\right]_0^\frac{\pi}{4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-339fc2c435d18fcb293b1915b66c271a_l3.png)
I = ![Rendered by QuickLaTeX.com \left[attan^2t-atant+at\right]_0^\frac{\pi}{4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-388d1c937816fe5013d5db0f4d6c862e_l3.png)
I = 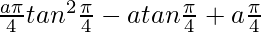
I = 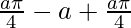
I = 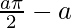
I = 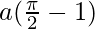
Therefore, the value of 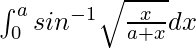 is
is 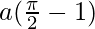 .
.
Question 53. 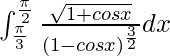
Solution:
We have,
I = 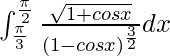
I = 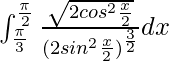
I = 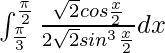
I = 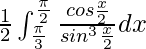
I = 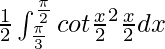
Let cot x/2 = t. So, we have
=>  = dt
= dt
Now, the lower limit is, x = π/3
=> t = cot x/2
=> t = cot π/6
=> t = √3
Also, the upper limit is, x = π/2
=> t = cot x/2
=> t = cot π/4
=> t = 1
So, the equation becomes,
I = 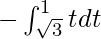
I = 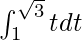
I = ![Rendered by QuickLaTeX.com \left[\frac{t^2}{2}\right]^{\sqrt{3}}_{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fb34ed0542318b4d6b3297735930007c_l3.png)
I = 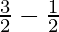
I = 1
Therefore, the value of 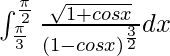 is 1.
is 1.
Question 54. 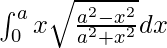
Solution:
We have,
I = 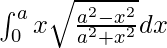
Let x2 = a2 cos 2t. So, we have
=> 2x dx = – 2a2 sin 2t dt
Now, the lower limit is, x = 0
=> a2 cos 2t = x2
=> a2 cos 2t = 0
=> cos 2t = 0
=> 2t = π/2
=> t = π/4
Also, the upper limit is, x = a
=> a2 cos 2t = x2
=> a2 cos 2t = a2
=> cos 2t = 1
=> 2t = 0
=> t = 0
So, the equation becomes,
I = 
I = 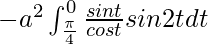
I = 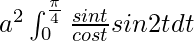
I = 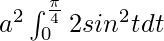
I = 
I = ![Rendered by QuickLaTeX.com a^2\left[t-\frac{sin2t}{2}\right]^{\frac{\pi}{4}}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bdc88532ea96cf0c45798682b41646f1_l3.png)
I = 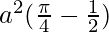
Therefore, the value of 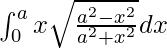 is
is 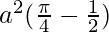 .
.
Question 55. 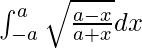
Solution:
We have,
I = 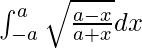
Let x = a cos 2t. So, we have
=> dx = –2a sin 2t
Now, the lower limit is, x = –a
=> a cos 2t = x
=> a cos 2t = –a
=> cos 2t = –1
=> 2t = π
=> t = π/2
Also, the upper limit is, x = a
=> a cos 2t = x
=> a cos 2t = a
=> cos 2t = 1
=> 2t = 0
=> t = 0
So, the equation becomes,
I = 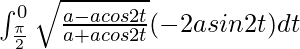
I = 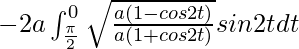
I = 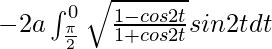
I = 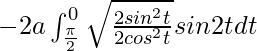
I = 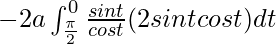
I = 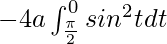
I = 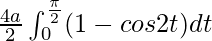
I = 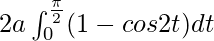
I = ![Rendered by QuickLaTeX.com 2a\left[t-\frac{sin2t}{2}\right]^{\frac{\pi}{2}}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-36be1e1e83ec2cb4f6d74db35f3ddfd9_l3.png)
I = ![Rendered by QuickLaTeX.com 2a\left[\frac{\pi}{2}-0-0+0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-35c7713f6685fbe359cacaf04765e671_l3.png)
I = πa
Therefore, the value of 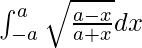 is πa.
is πa.
Question 56. 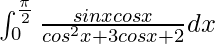
Solution:
We have,
I = 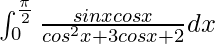
Let cos x = t. So, we have
=> – sin x dx = dt
=> sin x dx = –dt
Now, the lower limit is, x = 0
=> t = cos x
=> t = cos 0
=> t = 1
Also, the upper limit is, x = π/2
=> t = cos x
=> t = cos π/2
=> t = 0
So, the equation becomes,
I = 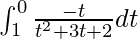
I = 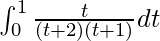
I = 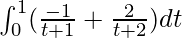
I = ![Rendered by QuickLaTeX.com \left[-log|1+t|+2log|t+2|\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ec8baff5fe19ee192ad664218ab0acb_l3.png)
I = – log 2 + 2 log 3 + 0 – 2 log 2
I = 2 log 3 – 3 log 2
I = log 9 – log 8
I = log 9/8
Therefore, the value of 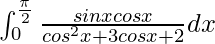 is log 9/8.
is log 9/8.
Question 57. 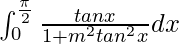
Solution:
We have,
I = 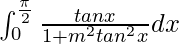
I = 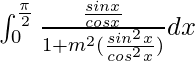
I = 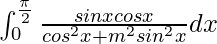
Let sin2 x = t. So, we have
=> 2 sin x cos x dx = dt
Now, the lower limit is, x = 0
=> t = sin2 x
=> t = sin2 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = sin2 x
=> t = sin2 π/2
=> t = 1
So, the equation becomes,
I = 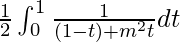
I = 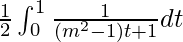
I = ![Rendered by QuickLaTeX.com \frac{1}{2(m^2-1)}\left[\log|(m^2-1)t+1|\right]_0^1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-11e8ed570d9e3db6e2331ed6043471b1_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{2(m^2-1)}\left[\log|m^2-1+1|-log1\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-80b71f0cf13dbc39a4eea8963e70ad39_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{2(m^2-1)}\left[\log m^2-log1\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-75634d5e94c4fd377b341b3e51499e69_l3.png)
I = 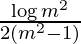
I = 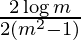
I = 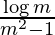
Therefore, the value of  is
is 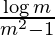 .
.
Question 58. 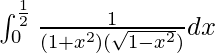
Solution:
We have,
I = 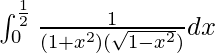
Let x = sin t. So, we have
=> dx = cos t dt
Now, the lower limit is, x = 0
=> sin t = x
=> sin t = 0
=> t = 0
Also, the upper limit is, x = 1/2
=> sin t = x
=> sin t = 1/2
=> t = π/6
So, the equation becomes,
I = 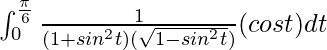
I = 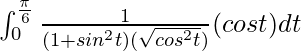
I = 
I = 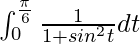
I = 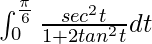
Let tan t = u. So, we have
=> sec2 t dt = du
Now, the lower limit is, t = 0
=> u = tan t
=> u = tan 0
=> t = 0
Also, the upper limit is, t = π/6
=> u = tan t
=> u = tan π/6
=> t = 1/√3
So, the equation becomes,
I = 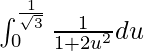
I = ![Rendered by QuickLaTeX.com \frac{1}{\sqrt{2}}\left[tan^{-1}(\sqrt{2}u)\right]_{0}^{\frac{1}{\sqrt{3}}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-20ac359767f60a654802ca43b1e6fb23_l3.png)
I = 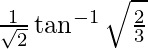
Therefore, the value of 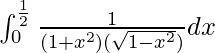 is
is 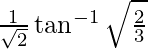 .
.
Question 59. 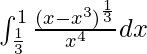
Solution:
We have,
I = 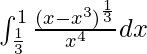
Let 1/x2 – 1 = t. So, we have
=> –2/x3 dx = dt
Now, the lower limit is, x = 1/3
=> t = 1/x2 – 1
=> t = 9 – 1
=> t = 8
Also, the upper limit is, x = 1
=> t = 1/x2 – 1
=> t = 1 – 1
=> t = 0
So, the equation becomes,
I = 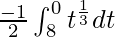
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{t^{\frac{4}{3}}}{\frac{4}{3}}\right]_{0}^{8}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7d062a71130f22adcd0a1a7a7c433fa9_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{3}{8}\left[t^{\frac{4}{3}}\right]_{0}^{8}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d1a13d1f97d33c0698e24d58eb033328_l3.png)
I = 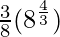
I = 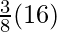
I = 6
Therefore, the value of 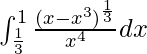 is 6.
is 6.
Question 60. 
Solution:
We have,
I = 
I = 
Let tan x = t. So, we have
=> sec2 x dx = dt
Now, the lower limit is, x = 0
=> t = tan t
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π/4
=> t = tan t
=> t = tan π/4
=> t = 1
So, the equation becomes,
I = 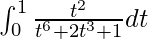
Let t3 = u. So, we have
=> 3t2 dt = du
=> t2 dt = du/3
Now, the lower limit is, t = 0
=> u = t3
=> u = 03
=> u = 0
Also, the upper limit is, t = 1
=> u = t3
=> u = 13
=> u = 1
So, the equation becomes,
I = 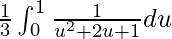
I = 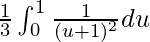
I = ![Rendered by QuickLaTeX.com \frac{1}{3}\left[\frac{-1}{u+1}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ef15c8cdfe4df64fc03a34829f3ffca_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{3}\left[\frac{-1}{1+1}+\frac{1}{1+0}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4e596c7eb420bda8b0bdd0b76ab56571_l3.png)
I = 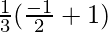
I = 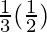
I = 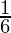
Therefore, the value of 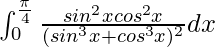 is
is 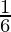 .
.
Question 61. 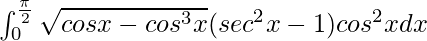
Solution:
We have,
I = 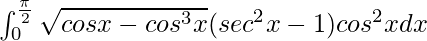
I = 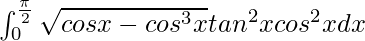
I = 
I = 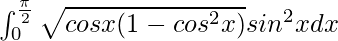
I = 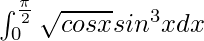
Let cos x = t. So, we have
=> – sin x dx = dt
Now, the lower limit is, x = 0
=> t = cos x
=> t = cos 0
=> t = 1
Also, the upper limit is, x = π/2
=> t = cos x
=> t = cos π/2
=> t = 0
So, the equation becomes,
I = 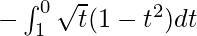
I = 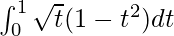
I = 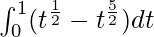
I = ![Rendered by QuickLaTeX.com \left[\frac{2t^{\frac{3}{2}}}{3}-\frac{2t^{\frac{7}{2}}}{7}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d5a0f25046aead42022db3e18c87a88f_l3.png)
I = 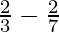
I = 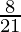
Therefore, the value of  is
is 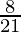 .
.
Question 62. 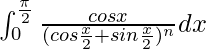
Solution:
We have,
I = 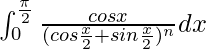
I = 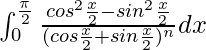
I = 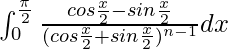
Let cos x/2 + sin x/2 = t. So, we have
=> (cos x/2 – sin x/2) dx = 2 dt
Now, the lower limit is, x = 0
=> t = cos x/2 + sin x/2
=> t = cos 0 + sin 0
=> t = 1 + 0
=> t = 1
Also, the upper limit is, x = π/2
=> t = cos x/2 + sin x/2
=> t = cos π/2 + sin π/2
=> t = 1/√2 + 1/√2
=> t = √2
So, the equation becomes,
I = 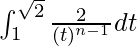
I = ![Rendered by QuickLaTeX.com \left[\frac{2t^{-n+2}}{-n+2}\right]_{1}^{\sqrt{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7339548b1f910375dd53748ad7a974d9_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{2}{2-n}\left[(\sqrt{2})^{2-n}-1\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d1a41424aae04e5ab12074f17f2ef7ed_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{2}{2-n}\left[2^{1-\frac{n}{2}}-1\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b2549ed038941e0f6e0b2c25e0a89550_l3.png)
Therefore, the value of 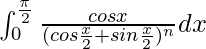 is
is ![Rendered by QuickLaTeX.com \frac{2}{2-n}\left[2^{1-\frac{n}{2}}-1\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5be232cec4c69294f4a70ca3a349224b_l3.png) .
.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...