Question 1. Show that the points whose position vectors are given are collinear:
(i) 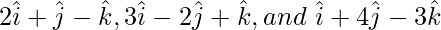
Solution:
Let x = 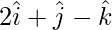
y = 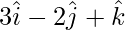
z = 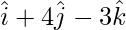
Then
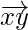 = Position vector of (y) – Position vector of (x)
= Position vector of (y) – Position vector of (x)
= 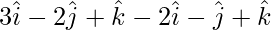
= 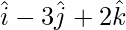
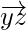 = Position vector of (z) – Position vector of (y)
= Position vector of (z) – Position vector of (y)
= 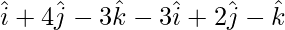
= 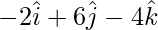
As, 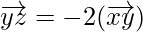
So, 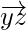 and
and 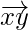 are parallel vectors but y is a common point to them. Hence, the given points x, y, z are collinear.
are parallel vectors but y is a common point to them. Hence, the given points x, y, z are collinear.
(ii) 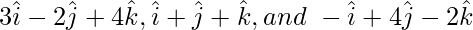
Solution:
Let
x = 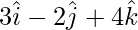
y = 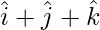
z = 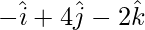
Then,
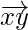 = Position vector of (y) – Position vector of (x)
= Position vector of (y) – Position vector of (x)
= 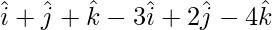
= 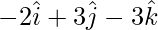
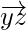 = Position vector of (z) – Position vector of (y)
= Position vector of (z) – Position vector of (y)
= 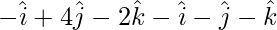
= 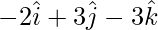
As, 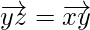
So, 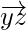 and
and 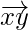 are parallel vectors but y is a common point to them. Hence, the given points x, y, z are collinear.
are parallel vectors but y is a common point to them. Hence, the given points x, y, z are collinear.
Question 2 (i). Using vector method, prove that A(6, -7, -1), B(2, -3, 1), and C(4, -5, 0) are collinear.
Solution:
The points given are A(6, -7, -1), B(2, -3, 1), and C(4, -5, 0)
So, 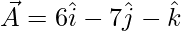
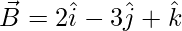
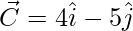
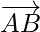 = Position vector of (B) – Position vector of (A)
= Position vector of (B) – Position vector of (A)
= 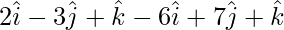
= 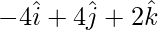
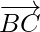 = Position vector of (C) – Position vector of (B)
= Position vector of (C) – Position vector of (B)
=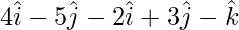
= 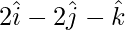
As, 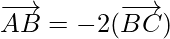
So, 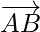 and
and 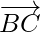 are parallel vectors but B is a common point to them. Hence, the given points A, B, C are collinear.
are parallel vectors but B is a common point to them. Hence, the given points A, B, C are collinear.
Question 2 (ii). Using vector method, prove that A(2, -1, 3), B(4, 3, 1), and C(3, 1, 2) are collinear.
Solution:
The points given are A(2, -1, 3), B(4, 3, 1), C(3, 1, 2)
So, the 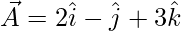
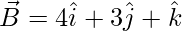
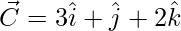
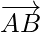 = Position vector of (B) – Position vector of (A)
= Position vector of (B) – Position vector of (A)
= 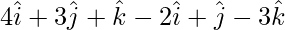
= 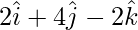
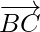 = Position vector of (C) – Position vector of (B)
= Position vector of (C) – Position vector of (B)
= 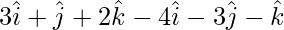
= 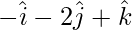
As, 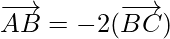
So, 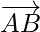 and
and 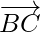 are parallel vectors but B is a common point to them. Hence, the given points A, B, C are collinear.
are parallel vectors but B is a common point to them. Hence, the given points A, B, C are collinear.
Question 2 (iii). Using vector method, prove that X(1, 2, 7), Y(2, 6, 3), and Z(3, 10, -1) are collinear.
Solution:
The points given are X(1, 2, 7), Y(2, 6, 3), Z(3, 10, -1).
So, the 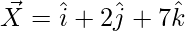
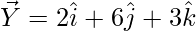
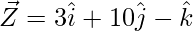
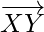 = Position vector of (Y) – Position vector of (X)
= Position vector of (Y) – Position vector of (X)
= 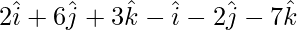
= 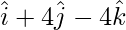
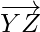 = = Position vector of (Z) – Position vector of (Y)
= = Position vector of (Z) – Position vector of (Y)
= 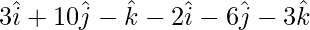
= 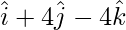
As, 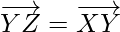
So, 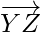 and
and 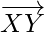 are parallel vectors but Y is a common point to them. Hence, the given points X, Y, Z are collinear.
are parallel vectors but Y is a common point to them. Hence, the given points X, Y, Z are collinear.
Question 2 (iv). Using vector method, prove that X(-3, -2, -5), Y(1, 2, 3), and Z(3, 4, 7) are collinear.
Solution:
The given points are X(-3, -2, -5), Y(1, 2, 3), and Z(3, 4, 7)
So, 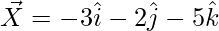
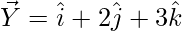
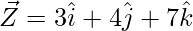
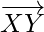 = Position vector of (Y) – Position vector of (X)
= Position vector of (Y) – Position vector of (X)
= 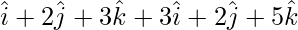
= 
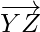 = = Position vector of (Z) – Position vector of (Y)
= = Position vector of (Z) – Position vector of (Y)
= 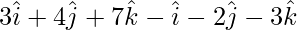
= 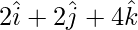
As, 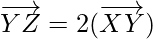
So, 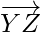 and
and 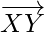 are parallel vectors but Y is a common point to them. Hence, the given points X, Y, Z are collinear.
are parallel vectors but Y is a common point to them. Hence, the given points X, Y, Z are collinear.
Question 2 (v). Using vector method, prove that X(2, -1, 3), Y(3, -5, 1), and Z(-1, 11, 9) are collinear.
Solution:
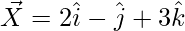
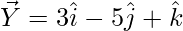
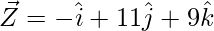
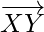 = Position vector of (Y) – Position vector of (X)
= Position vector of (Y) – Position vector of (X)
= 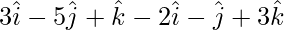
= 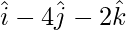
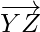 = = Position vector of (Z) – Position vector of (Y)
= = Position vector of (Z) – Position vector of (Y)
= 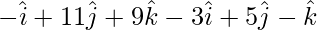
= 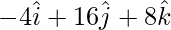
As, 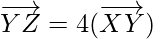
So, 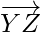 and
and 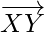 are parallel vectors but Y is a common point to them. Hence, the given points X, Y, Z are collinear.
are parallel vectors but Y is a common point to them. Hence, the given points X, Y, Z are collinear.
Question 3 (i). If 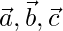 are non-zero, non-coplaner vectors, prove that the vectors
are non-zero, non-coplaner vectors, prove that the vectors 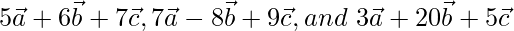 are coplanar.
are coplanar.
Solution:
The given vectors are
X = 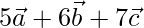
Y = 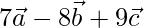
Z = 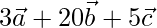
Three vectors are coplanar, if they satisfy the given conditions(for real u and v)
X = u * Y + v * Z
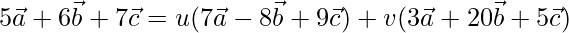
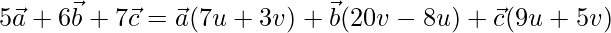
On comparing coefficients, we get the following equations
7u + 3v = 5 -(1)
20v – 8u = 6 -(2)
9u + 5v = 7 -(3)
From first two equations, we find that
u = 1/2
v = 1/2
Now put the value of u and v in eq(3)
9(1/2) + 5(1/2) = 7
14/2 = 7
7 = 7
So, the value satisfies the third equation.
Hence, the given vectors X, Y, Z are coplanar.
Question 3 (ii). If 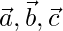 are non-zero, non-coplaner vectors, prove that the vectors
are non-zero, non-coplaner vectors, prove that the vectors 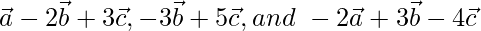 are coplanar.
are coplanar.
Solution:
The given vectors are
X = 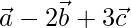
Y = 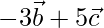
Z = 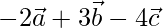
Three vectors are coplanar, if they satisfy the given conditions(for real u and v)
X = u * Y + v * Z
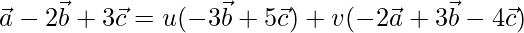
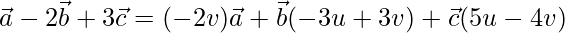
On comparing coefficients, we get the following equations
-2v = 1 -(1)
3v – 3u = -2 -(2)
5u – 4v = 3 -(3)
From the first two equations, we find that
v = -1/2
u = 1/6
Now put the value of u and v in eq(3)
5(1/6) – 4(-1/2) = 3
5/6 + 2 = 3
(5 + 12)/6 = 3
17/6 ≠ 3
The value doesn’t satisfy the third equation. Hence, the given vectors X, Y, Z are not coplanar.
Question 4.Show that the four points having position vectors 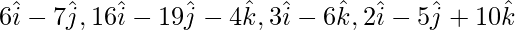 are coplanar.
are coplanar.
Solution:
Let the given vectors be
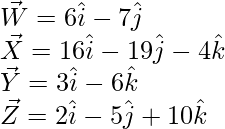
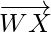 = Position vector of (X) – Position vector of (W)
= Position vector of (X) – Position vector of (W)
= 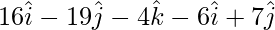
= 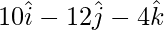
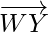 = Position vector of (Y) – Position vector of (W)
= Position vector of (Y) – Position vector of (W)
=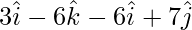
= 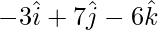
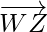 = Position vector of (Z) – Position vector of (W)
= Position vector of (Z) – Position vector of (W)
= 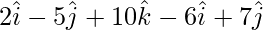
= 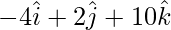
The given vectors are coplanar if,
WX = u(WY) + v(WZ)
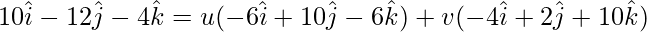
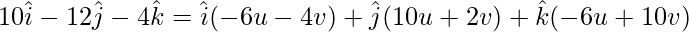
On comparing coefficients, we get the following equations
-6u – 4v = 10 -(1)
10u + 2v = -12 -(2)
-6u + 10v = -4 -(3)
From the first two equations, we find that
u = -1
v = -1
Now put the value of u and v in eq(3)
-6(-1) + 10(-1) = -4
6 – 10 = -4
-4 = -4
The value satisfies the third equation. Hence, the given vectors W, X, Y, Z are coplanar.
Question 5(i). Prove that the following vectors are coplanar Show that the points 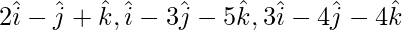
Solution:
The given vectors are 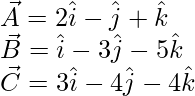
The given vectors are coplanar if,
A = u(B) + v(C)
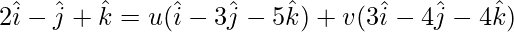
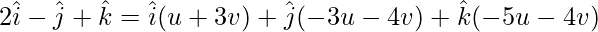
On comparing coefficients, we get the following equations
u + 3v = 2 -(1)
-3u – 4v = -1 -(2)
-5u – 4v = 1 -(3)
From the first two equations, we find that
u = -1
v = 1
Now put the value of u and v in eq(3)
-5(-1) – 4(1) = 1
5 – 4 = 1
1 = 1
The value satisfies the third equation. Hence, the given vectors A, B, C are coplanar.
Question 5(ii). Prove that the following vectors are coplanar Show that the points 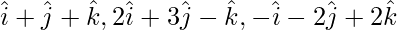
Solution:
The given vectors are 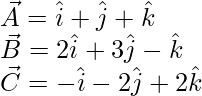
The given vectors are coplanar if,
A = u(B) + v(C)
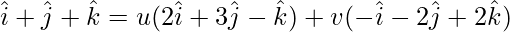
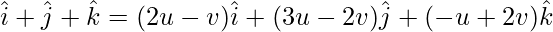
On comparing coefficients, we get the following equations
2u – v = 1 -(1)
3u – 2v = 1 -(2)
-u + 2v = 1 -(3)
From the first two equations, we find that
u = 1
v = 1
Now put the value of u and v in eq(3)
-(1) + 2(1) = 1
1 = 1
The value satisfies the third equation. Hence, the given vectors A, B, C are coplanar.
Question 6 (i). Prove that the vector 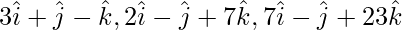 are non-coplanar.
are non-coplanar.
Solution:
The given vectors are 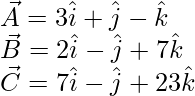
The given vectors are coplanar if,
A = u(B) + v(C)
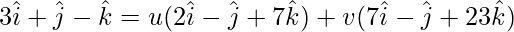
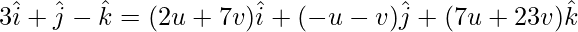
On comparing coefficients, we get the following equations
2u + 7v = 3 -(1)
-u – v = 1 -(2)
7u + 23v = -1 -(3)
From the first two equations, we find that
u = -2
v = 1
Now put the value of u and v in eq(3)
7(-2) + 23(1) = -1
-14 + 23 = -1
-9 ≠ -1
The value does not satisfy the third equation. Hence, the given vectors A, B, C are not coplanar.
Question 6 (ii). Prove that the vector 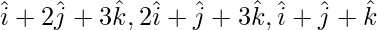 are non-coplanar.
are non-coplanar.
Solution:
The given vectors are 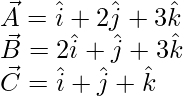
The given vectors are coplanar if,
A = u(B) + v(C)
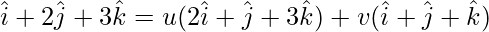
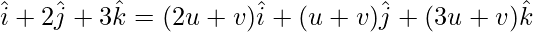
On comparing coefficients, we get the following equations
2u + v = 1 -(1)
u + v = 2 -(2)
3u + v = 3 -(3)
From the first two equations, we find that
u = 0
v = 1
Now put the value of u and v in eq(3)
3(0) + 1 = 3
1 = 3
The value does not satisfy the third equation. Hence, the given vectors A, B, C are not coplanar.
Question 7(i). If 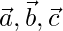 are non-coplanar vectors, prove that the given vectors are non-coplanar
are non-coplanar vectors, prove that the given vectors are non-coplanar 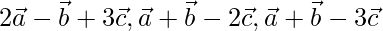
Solution:
The given vectors are 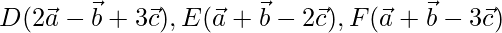 )
)
The given vectors are coplanar if,
D = u(E) + v(F)
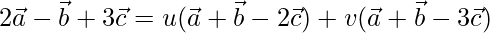
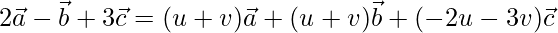
On comparing coefficients, we get the following equations
u + v = 2 -(1)
u + v = -1 -(2)
-2u – 3v = 3 -(3)
There is no value that satisfies the third equation. Hence, the given vectors D, E, F are not coplanar.
Question 7(ii). If 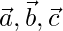 are non-coplanar vectors, prove that the given vectors are non-coplanar
are non-coplanar vectors, prove that the given vectors are non-coplanar 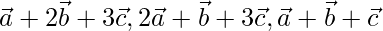
Solution:
The given vectors are 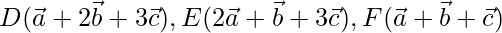
The given vectors are coplanar if,
D = u(E) + v(F)
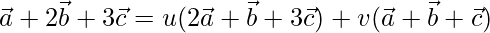
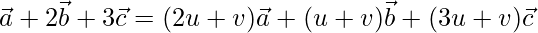
On comparing coefficients, we get the following equations
2u + v = 1 -(1)
u + v = 2 -(2)
3u + v = 3 -(3)
From the first two equations, we find that
u = -1
v = 3
Now put the value of u and v in eq(3)
3(-1) + (3) = 3
0 = 3
There is no value that satisfies the third equation. Hence, the given vectors D, E, F are not coplanar.
Question 8. Show that the vector 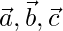 given by
given by 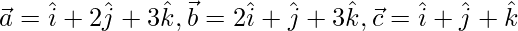 are non-coplanar. Express vector \vec{d} =
are non-coplanar. Express vector \vec{d} =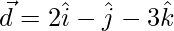 as a linear combination of the vector
as a linear combination of the vector 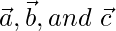 .
.
Solution:
The given vectors are
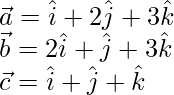
The given vectors are coplanar if,
D = u(E) + v(F)
On comparing coefficients, we get the following equations
2u + v = 1 -(1)
u + v = 2 -(2)
3u + v = 3 -(3)
From above two equations,
u = -1
v = 3
Now put the value of u and v in eq(3)
3(-1) + (3) = 3
0 = -3
There is no value that satisfies the third equation. Hence, the given vectors D, E, F are not coplanar
The given vectors are
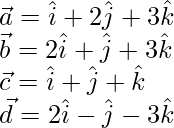
The given vectors are coplanar if,
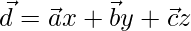
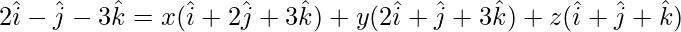
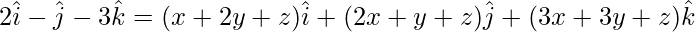
On comparing coefficients, we get the following equations,
x + 2y + z = 2 -(1)
2x + y + z = -1 -(2)
3x + 3y + z = -3 -(3)
From above three equations,
x = -8/3
y = 1/3
z = 4
Therefore, 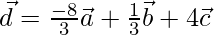
Question 9. Prove that a necessary and sufficient condition for the three vectors 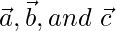 to be coplanar is that these exist scalar l, m, n, not all zero simultaneously such that
to be coplanar is that these exist scalar l, m, n, not all zero simultaneously such that 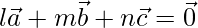
Solution:
Given conditions: Let us considered 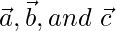 be three coplanar vectors.
be three coplanar vectors.
Then one of them is expressible as a linear combination of other two vectors.
Let,
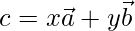
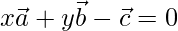
Here, l = x, y = m, n = -1
From above,
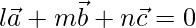
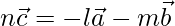
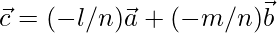
Hence, 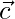 is a linear combination of two vectors
is a linear combination of two vectors 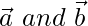 .
.
Hence proved that 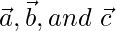 are coplanar vectors.
are coplanar vectors.
Question 10. Show that the four points A, B, C, and D with position vectors 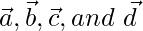 respectively are coplanar if and only if
respectively are coplanar if and only if 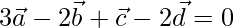 .
.
Solution:
Given: A, B, C, D be four vectors with position vector 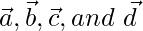
Let us considered A, B, C, D be coplanar.
Then, there exists x, y, z, u not all zero such that,
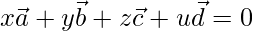
Let us considered x = 3, y = -2, z = 1, y = -2
So, 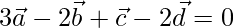
and x + y + z + u = 3 – 2 + 1 – 2 = 0
So, A, B, C, D are coplanar.
Let us considered 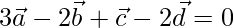
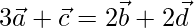
Now on dividing both side by sum of coefficient 4
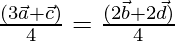
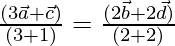
It shows that point P divides AC in the ratio 1:3 and BD in the ratio 2:2 internally,
hence P is the point of intersection of AC and BD.
So, A, B, C, D are coplanar.
Share your thoughts in the comments
Please Login to comment...