Class 12 RD Sharma Solutions – Chapter 21 Areas of Bounded Regions – Exercise 21.1 | Set 2

Last Updated : 20 May, 2021

Question 11. Sketch the region {(x, y) : 9x² + 4y² = 36} and find the area enclosed by it, using integration.

Solution:

9×2 + 4y2 = 36

$\frac{x^2}{4}+\frac{y^2}{9}=1\\ y=\pm\sqrt{\frac{36-9x^2}{4}}$

Area of Sector OABCO = $\displaystyle \int_0^2\sqrt{\frac{36-9x^2}{4}}\ dx\\ =\frac{3}{2}\int_0^2\sqrt{4-x^2}\ dx\\ =\frac{3}{2}\left[\frac{x\sqrt{4-x^2}}{2}+\frac{2^2}{2}sin^{-1}\left(\frac{x}{2}\right)\right]_0^2\\ =\frac{3}{2}\left[\frac{2\sqrt{4-2^2}}{2}+\frac{2^2}{2}sin^{-1}\left(\frac{2}{2}\right)\right]-\frac{3}{2}\left[\frac{0\sqrt{4-0^2}}{2}+\frac{2^2}{2}sin^{-1}\left(\frac{0}{2}\right)\right]\\ =\frac{3}{2}\times2\times\frac{\pi}{2}-0\\ =\frac{3\pi}{2}\ sq.\ units$

Area of the whole figure = 4 x area of DOABCO

$=4\times\frac{3\pi}{2}\\ =6\pi\ sq.\ units.$

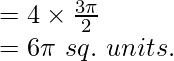
Question 12. Draw a rough sketch of the graph of the function $y=2\sqrt{1-x^2}$ , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis

Solution:

Here, we have to find the area enclosed between the curve and x-axis.

$y=2\sqrt{1-x^2},\ x\ ∈\ [0,\ 1 ]\\ \Rightarrow y^2+4x^2=4,\ x\ ∈\ [0,\ 1]\\ \Rightarrow \frac{x^2}{1}+\frac{y^2}{4},\ x\ ∈\ [0,\ 1]$

Equation (1) represents an ellipse with centre at origin and passes through (±1, 0) and (0, ±2) and x ∈ [0, 1] as represented by region between y-axis and line x = 1.

Here, is the rough sketch.

Shaded region represents the required area.

We slice it into approximation rectangle of

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 0 to x = 1,

Thus,

Required area = Region OAPBO

$\displaystyle =\int_0^1y\ dx\\ =\int_0^12\sqrt{1-x^2}\ dx\\ =2\left[\frac{x}{2}\sqrt{1-x^2}+\frac{1}{2}sin^{-1}(x)\right]_0^1\\ =2\left[\left(\frac{1}{2}\sqrt{1-x^2}+\frac{1}{2}sin^{-1}(1)\right)-(0+0)\right]\\ =2\left[0+\frac{1}{2}\times\frac{\pi}{2}\right]$

Required area = $\frac{\pi}{2}$ square units

Question 13. Determine the area under the curve 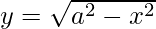$y=\sqrt{a^2-x^2}$ included between the line x = 0 and x = 8.

Solution:

Here,

We have to find area under the curve

$y =\sqrt{a^2-x^2}$

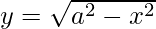
x2 + y2 = a ………..(1)

between x = 0 ………(2)

x = a ………..(3)

Equation (1) represents a circle with Centre (0, 0) and passes axes at (0, ±a), (±a, 0).

Equation (2) represents y-axis and

Equation x = a represents a line parallel to y-axis passing through (a, 0)

Here, is the rough sketch,

Shaded region represents the required area.

We slice it into approximation rectangle of

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 0 to x = a,

Thus,

Required area = Region OAPBO

$\displaystyle =\int_0^ay\ dx\\ =\int_0^a\sqrt{a^2-x^2}\ dx\\ =\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{a}\right]_0^a\\ =\left[\left(\frac{a}{2}\sqrt{a^2-a^2}+\frac{a^2}{2}sin^{-1}(1)\right)-(0)\right]\\ =2\left[0+\frac{a^2}{2}\times\frac{\pi}{2}\right]$

Required area = 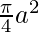$\frac{\pi}{4}a^2$ square units

Question 14. Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8

Solution:

Here,

We have to find area bounded by x-axis

2y + 5x = 7 ………(1)

x = 2 ……..(2)

x = 8 ………(3)

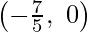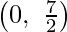Equation (1) represents line passing through $\left(-\frac{7}{5},\ 0\right)$ and $\left(0,\ \frac{7}{2}\right)$ equation.

Equation (2), (3) shows line parallel to y-axis passing through (2, 0), (8, 0) respectively.

Here, is the rough sketch;

Shaded region represents the required area.

We slice it into approximation rectangle of

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 2 to x = 8,

Thus,

Required area = Region ABCDA

$\displaystyle =\int_2^8\left(\frac{5x+7}{2}\right)\\ =\frac{1}{2}\left(\frac{5x^2}{2}+7x\right)_2^8\\ =\frac{1}{2}\left[\left(\frac{5(8)^2}{2}+7(8)\right)-\left(\frac{5(2)^2}{2}+7(2)\right)\right]\\ =\frac{1}{2}[(160+56)-(10+14)]\\ =\frac{192}{2}$

Required area = 96 square units

Question 15. Using definite integrals, find the area of the circle x² + y² = a²

Solution:

Here, we have to find the area of circle,

x2 + y2 = a2

Equation (1) represents a circle with centre (0, 0) and radius a, Thus is meets the axes (±a, 0), (0, ±a).

Here, is the rough sketch;

Shaded region represents the required area.

We slice it into approximation rectangle of

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 0 to x = a,

Thus,

Required area = Region ABCDA

= 4 ( Region ABOA)

$\displaystyle =4\int_0^ay\ dx\\ =4\int_0^a\sqrt{a^2-x^2}\ dx\\ =4\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{a}\right]_0^a\\ =4\left[\left(\frac{a}{2}\sqrt{a^2-a^2}+\frac{a^2}{2}sin^{-1}(1)\right)-(0+0)\right]\\ =4\left[0+\frac{a^2}{2}\times\frac{\pi}{2}\right]\\ =4\left(\frac{a^2\pi}{4}\right)$

Question 16. Using the integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + |x + 1|, x = -2, x = 3, y =

Solution:

Here, we have to find the area enclosed by;

x = -2,

x = 3,

y = 0 and

y = 1 + |x + 1|

⇒ y = 1 + x + 1, if x + 1 0

⇒ y = 2 + x ……….(1), if x ≥ -1

and

⇒ y = 1 – (x + 1), if x + 1 < 0

⇒ y = 1 – x – 1, if x < -1

⇒ y = -x ………(2), if x < -1

Thus,

Equation (1) is a straight line that passes through (0, 2) and (-1 , 1).

Equation (2) is a line passing through (-1, 1) and (-2, 2) and it is enclosed by line x = 2 and x = 3 which are lines parallel to y-axis and pass through (2, 0) and (3, 0) respectively y = 0 is x-axis

Here is the rough sketch

Shaded region represents the required area.

Thus,

Required area = Region (ABECDFA)

Required area = (Region ABEFA + Region ECDFE) ……..(1)

Region ECDFE

We slice it into approximation rectangle of

Width = △x

Length = y1

Area of rectangle = y1△x

The approx rectangles slide from x = -2 to x = -1,

Region ABEFA

We slice it into approximation rectangle of

Width = △x

Length = y2

Area of rectangle = y2△x

The approx rectangles slide from x = -1 to x = 3,

Required area = $\displaystyle \int_{-2}^{-1}y_1\ dx+\int_{-1}^3y_2\ dx\\ =-\left[\frac{x^2}{2}\right]^{-1}_{-2}+\left[\frac{x^2}{2}+2x\right]_{-1}^3\\ =-\left[\frac{1}{2}+\frac{4}{2}\right]+\left[\left(\frac{9}{2}+6\right)-\left(\frac{1}{2}-2\right)\right]\\ =\frac{3}{2}+\left(\frac{21}{2}+\frac{3}{2}\right)\\ =\frac{27}{2}$

Required area = $\frac{27}{2}$ square units

Question 17. Sketch the graph y = |x -5|. Evaluate 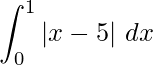$\displaystyle \int_0^1|x-5|\ dx$ . What does the value of the integral represent on the graph?

Solution:

Here, is the sketch of the given graph:

y = |x – 5|

Hence,

Required area = $\displaystyle =\int_0^1y\ dx\\ =\int_0^1|x-5|\ dx\\ =\int_0^1-(x-5)\ dx\\ =\left[\frac{-x^2}{2}+5x\right]_0^1\\ =\left[-\frac{1}{2}+5\right]\\ =\frac{9}{2}\ sq.\ units$

Thus,

The given integral represents the area bounded by the curves that are,

x = 0,

y = 0,

x = 1

and

y = -(x – 5).

Question 18. Sketch the graph of y = |x + 3| and evaluate 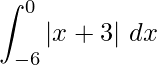$\displaystyle \int_{-6}^0|x+3|\ dx$ . What does this integral represents on the graph?

Solution:

Here,

The given equation is y = |x + 3|

The corresponding values of x and y are given in the following table.

x -6 -5 -4 -3 -2 -1 0
y 3 2 1 0 1 2 3

Thus,

After plotting these points,

We will get the graph of y = |x + 3|

It is shown as;

It is known that (x + 3) ≤ 0 for -6 ≤ x ≤ -3 and (x + 3) ≥ 0 for -3 ≤ x ≤ 0

Therefore,

$\displaystyle \int_{-6}^0|(x+3)|\ dx=-\int_{-6}^{-3}(x + 3)\ dx\\ =-\left[\frac{x^2}{2}+3x\right]_{-6}^{-3}+\left[\frac{x^2}{2}+3x\right]_{-3}^0\\ =\left[\left(\frac{(-3)^2}{2}+3(-3)\right)-\left(\frac{(-6)^2}{2}+3(-6)\right)\right]+\left[0-\frac{(-3)^2}{2}+3(-3)\right]\\ =-\left[-\frac{9}{2}\right]-\left[-\frac{9}{2}\right]\\ =9$

Question 19. Sketch the graph y = |x + 1|. Evaluate 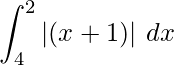$\displaystyle \int_{4}^2|(x+1)|\ dx$ . What does the value of this integral represent on this graph?

Solution:

Here,

Given:

y = |x + 1|=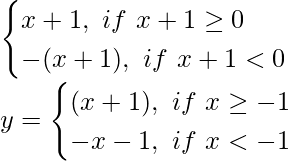 $\begin{cases} x+1,\ if\ x+1\ge 0\\ -(x+1),\ if\ x+1<0 \end{cases}\\ y=\begin{cases} (x+1),\ if\ x\ge -1\\ -x-1,\ if\ x<-1 \end{cases}$

y = x + 1 …………(1)

and

y = -x – 1 ……….(2)

Equation (1) represents a line which meets axes at (0, 1).

Equation (2) represents a line passing through (0, -1) and (-1, 0)

Here is the rough sketch

$\displaystyle \int_{4}^2|(x+1)|\ dx=-\int_{-4}^{-1}(x + 1)\ dx\ +\int_{-1}^2(x+1)\ dx\\ =-\left[\frac{x^2}{2}+x\right]_{-4}^{-1}+\left[\frac{x^2}{2}+x\right]_{-1}^2\\ =-\left[\left(\frac{1}{2}-1\right)-\left(\frac{16}{2}-4\right)\right]+\left[\left(\frac{4}{2}+2\right)-\left(\frac{1}{2}-1\right)\right]\\ =-\left[\left(-\frac{1}{2}-4\right)\right]+\left[4+\frac{1}{2}\right]\\ =\frac{9}{2}+\frac{9}{2}\\ =\frac{18}{2}$

Required area = 9 square units.

Question 20. Find the area of the region bounded by the curve xy – 3x – 2y – 10 = 0, x-axis and the lines x = 3, x = 4.

Solution:

Here,

We have to find the area bounded by

x axis,

x = 3,

x = 4

and

xy – 3x -2y – 10 = 0

⇒ y(x – 2) = 3x + 10

⇒ $y=\frac{3x+10}{x-2}$

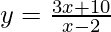
Here, is the rough sketch

Shaded region represents the required area.

We slice it into approximation rectangle of

Width = △x

Length = y

Area of rectangle = y△x

The approx rectangles slide from x = 3 to x = 4,

Required area = Region ABCDA

$\displaystyle =\int_3^4y\ dx\\ =\int_3^4\left(\frac{3x+10}{x-2}\right)\ dx\\ =\int_3^4\left(3+\frac{16}{x-2}\right)\ dx\\ =(3x)_3^4+16(log|x-2|)_3^4\\ =(12-9)+16(log2-log1)$

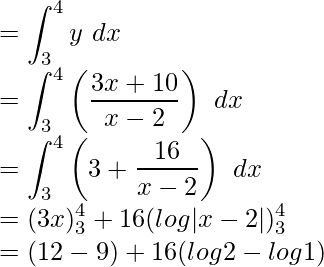
Required area = (3 + 16 log2) square units.

Suggest improvement

Class 12 RD Sharma Solutions - Chapter 21 Areas of Bounded Regions - Exercise 21.1 | Set 1

Class 12 RD Sharma Solutions - Chapter 21 Areas of Bounded Regions - Exercise 21.1 | Set 3

Share your thoughts in the comments

Chapter 1: Relations

Chapter 2: Functions

Chapter 3: Binary Operations

Chapter 4: Inverse Trigonometric Functions

Chapter 5: Algebra of Matrices

Chapter 6: Determinants

Chapter 7: Adjoint and Inverse of a Matrix

Chapter 8: Solutions of Simultaneous Linear Equations

Chapter 9: Continuity

Chapter 10: Differentiability

Chapter 11: Differentiation

Chapter 12: Higher Order Derivatives

Chapter 13: Derivative as a Rate Measurer

Chapter 14: Differentials, Errors, and Approximations

Chapter 15: Mean Value Theorems

Chapter 16: Tangents and Normals

Chapter 17: Increasing and Decreasing Functions

Chapter 18: Maxima and Minima

Chapter 19: Indefinite Integrals

Chapter 20: Definite Integrals

Chapter 21: Areas of Bounded Regions

Chapter 22: Differential Equations

Chapter 23: Algebra of Vectors

Chapter 24: Scalar Or Dot Product

Chapter 25: Vector or Cross Product

Chapter 26: Scalar Triple Product

Chapter 27: Direction Cosines and Direction Ratios

Chapter 28: Straight Line in Space

Chapter 29: The Plane

Chapter 30: Linear programming

Chapter 31: Probability

Chapter 32: Mean and Variance of a Random Variable

Chapter 33: Binomial Distribution

Chapter 1: Relations

Chapter 2: Functions

Chapter 3: Binary Operations

Chapter 4: Inverse Trigonometric Functions

Chapter 5: Algebra of Matrices

Chapter 6: Determinants

Chapter 7: Adjoint and Inverse of a Matrix

Chapter 8: Solutions of Simultaneous Linear Equations

Chapter 9: Continuity

Chapter 10: Differentiability

Chapter 11: Differentiation

Chapter 12: Higher Order Derivatives

Chapter 13: Derivative as a Rate Measurer

Chapter 14: Differentials, Errors, and Approximations

Chapter 15: Mean Value Theorems

Chapter 16: Tangents and Normals

Chapter 17: Increasing and Decreasing Functions

Chapter 18: Maxima and Minima

Chapter 19: Indefinite Integrals

Chapter 20: Definite Integrals

Chapter 21: Areas of Bounded Regions

Chapter 22: Differential Equations

Chapter 23: Algebra of Vectors

Chapter 24: Scalar Or Dot Product

Chapter 25: Vector or Cross Product

Chapter 26: Scalar Triple Product

Chapter 27: Direction Cosines and Direction Ratios

Chapter 28: Straight Line in Space

Chapter 29: The Plane

Chapter 30: Linear programming

Chapter 31: Probability

Chapter 32: Mean and Variance of a Random Variable

Chapter 33: Binomial Distribution

Class 12 RD Sharma Solutions – Chapter 21 Areas of Bounded Regions – Exercise 21.1 | Set 2

Question 11. Sketch the region {(x, y) : 9x2 + 4y2 = 36} and find the area enclosed by it, using integration.

Question 12. Draw a rough sketch of the graph of the function , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis

Question 13. Determine the area under the curve included between the line x = 0 and x = 8.

Question 14. Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8

Question 15. Using definite integrals, find the area of the circle x2 + y2 = a2

Question 16. Using the integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + |x + 1|, x = -2, x = 3, y =

Question 17. Sketch the graph y = |x -5|. Evaluate . What does the value of the integral represent on the graph?

Question 18. Sketch the graph of y = |x + 3| and evaluate . What does this integral represents on the graph?

Question 20. Find the area of the region bounded by the curve xy – 3x – 2y – 10 = 0, x-axis and the lines x = 3, x = 4.

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?

Question 11. Sketch the region {(x, y) : 9x² + 4y² = 36} and find the area enclosed by it, using integration.

Question 12. Draw a rough sketch of the graph of the function $y=2\sqrt{1-x^2}$ , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis

Question 13. Determine the area under the curve $y=\sqrt{a^2-x^2}$ included between the line x = 0 and x = 8.

Question 15. Using definite integrals, find the area of the circle x² + y² = a²

Question 17. Sketch the graph y = |x -5|. Evaluate $\displaystyle \int_0^1|x-5|\ dx$ . What does the value of the integral represent on the graph?

Question 18. Sketch the graph of y = |x + 3| and evaluate $\displaystyle \int_{-6}^0|x+3|\ dx$ . What does this integral represents on the graph?