Class 12 RD Sharma Solutions – Chapter 22 Differential Equations – Exercise 22.2 | Set 1
Last Updated :
16 Feb, 2022
Question 1. Form the differential equation of the family of curves represented by y2 = (x – c)3
Solution:
y2 = (x – c)3
On differentiating the given equation w.r.t x,
2y(dy/dx) = 3(x – c)2
(x – c)2 = (2y/3)(dy/dx)
(x – c) = [(2y/3)(dy/dx)]1/2 -(1)
On putting the value of (x – c) in equation (1), we get
y2 = [(2y/3)(dy/dx)]3/2
On squaring both side, we get
y4 = [(2y/3)(dy/dx)]3
y4 = (8y3/27)(dy/dx)3
27y4 = 8y3(dy/dx)3
27y = 8(dy/dx)3
Question 2. Form the differential equation corresponding to y = emx by eliminating m.
Solution:
y = emx -(1)
On differentiating the given equation w.r.t x,
dy/dx = memx -(2)
From eq(1), we get
y = emx
logy = mx
m = (logy/x)
Now, put the value of m in equation(2), we get
x(dy/dx) = ylogy
Question 3. Form the differential equations from the following primitives where constants are arbitrary.
(i) y2 = 4ax
Solution:
y2 = 4ax -(1)
y2/4x = a
On differentiating the given equation w.r.t x,
2y(dy/dx) = 4a -(2)
Now, put the value of a in equation(2), we get
2y(dy/dx) = 4(y2/4x)
2y(dy/dx) = y2/x
2x(dy/dx) = y
(ii) y = cx + 2c2 + c3
Solution:
y = cx + 2c2 + c3 -(1)
On differentiating the given equation w.r.t x,
dy/dx = c -(2)
Now, put the value of c in equation(1), we get
y = x(dy/dx) + 2(dy/dx)2 + (dy/dx)3
(iii) xy = a2
Solution:
xy = a2 -(1)
On differentiating the given equation w.r.t x,
x(dy/dx) + y = 0
(iv) y = ax2 + bx + c
Solution:
y = ax2 + bx + c -(1)
On differentiating the given equation w.r.t x,
dy/dx = 2ax + b -(2)
Again differentiating the given equation w.r.t x,
d2y/dx2 = 2a -(3)
Again, differentiating the given equation w.r.t x, we get
d3y/dx3 = 0
Question 4. Find the differential equation of the family of curves y = Ae2x + Be-2x where A and B are arbitrary constants.
Solution:
y = Ae2x + Be-2x -(1)
On differentiating the given equation w.r.t x,
(dy/dx) = 2Ae2x – 2Be-2x -(2)
Again, differentiating the given equation w.r.t x,
d2y/dx2 = 4Ae2x + 4Be-2x
d2y/dx2 = 4(Ae2x + Be-2x)
d2y/dx2 = 4y
Question 5. Find the differential equation of the family of curves, x = Aconst + Bsinnt where A and B are arbitrary constants.
Solution:
x = Acosnt + Bsinnt -(1)
On differentiating the given equation w.r.t x,
dy/dx = -Ansinnt + Bncosnt -(2)
Again, differentiating the given equation w.r.t x,
d2y/dx2 = -An2cosnt – Bn2sinnt
d2y/dx2 = -n2(Acosnt + Bsinnt)
d2y/dx2 + n2x = 0
Question 6. Form the differential equation corresponding to y2 = a(b – x2) by eliminating a and b.
Solution:
y2 = a(b – x2)
On differentiating the given equation w.r.t x,
2y(dy/dx) = a(0 – 2x)
Again, differentiating the given equation w.r.t x,
![Rendered by QuickLaTeX.com 2[y\frac{d^2y}{dx^2}+(\frac{dy}{dx})^2]=-2a](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-11d77894da6eeb4b61c9b94afb7b1be7_l3.png)
![Rendered by QuickLaTeX.com [y\frac{d^2y}{dx^2}+(\frac{dy}{dx})^2]=-(\frac{y}{-x}*\frac{dy}{dx})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4fcfac07704c444b892ec8fd8be480c7_l3.png)
x[![Rendered by QuickLaTeX.com x[y\frac{d^2y}{dx^2}+(\frac{dy}{dx})^2]=y\frac{dy}{dx}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0dc7964d82ca9dcead63dfce609255c9_l3.png)
Question 7. Form the differential equation corresponding to y2 – 2ay + x2 = a2 by eliminating a.
Solution:
y2 – 2ay + x2 = a2 -(1)
On differentiating the given equation w.r.t x,
2y(dy/dx) – 2a(dy/dx) + 2x = 0
2y(dy/dx) + 2x = 2a(dy/dx)
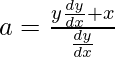 -(2)
-(2)
Let us considered dy/dx = y’
On putting the value of ‘a’ in the eq(1), we get
![Rendered by QuickLaTeX.com y^2-2[\frac{y\frac{dy}{dx}+x}{\frac{dy}{dx}}]y+x^2=[\frac{y\frac{dy}{dx}+x}{\frac{dy}{dx}}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-06c8c3b3b7d7f144e3c425a9e67bbce8_l3.png)
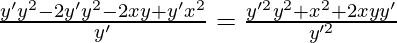
On solving this equation, we get
(x2 – 2y2)y’2 – 4xyy’ – x2 = 0
(x2 – 2y2)(dy/dx)2 – 4xy(dy/dx) – x2 = 0
Question 8. Form the differential equation corresponding to (x – a)2 + (y – b)2 = r2 by eliminating a and b.
Solution:
(x – a)2 + (y – b)2 = r2 -(1)
On differentiating the given equation w.r.t x,
2(x – a) + 2(y – b)(dy/dx) = 0
(x – a) + (y – b)(dy/dx) = 0 -(2)
Again, differentiating the given equation w.r.t x,
1 + (y – b)(d2y/dx2) + (dy/dx)(dy/dx) = 0
![Rendered by QuickLaTeX.com (y-b)=-[\frac{(\frac{dy}{dx})^2+1}{\frac{d^2y}{dx^2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-396de4a21f70ac45bc43b1c98bfc9f2f_l3.png) -(3)
-(3)
On putting the value of (y – b) in eq(2),
![Rendered by QuickLaTeX.com (x-a)-[\frac{(\frac{dy}{dx})^2+1}{\frac{d^2y}{dx^2}}]\frac{dy}{dx}=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5388ca8e8337369b849f6ab0e2c6fdb6_l3.png)
(x – a)(d2y/dx2) – (dy/dx)3 – (dy/dx) = 0
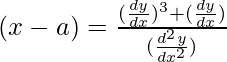 -(4)
-(4)
On putting the value of (x – a) and (y – b) in eq(1)
![Rendered by QuickLaTeX.com [\frac{(\frac{dy}{dx})^3+(\frac{dy}{dx})}{(\frac{d^2y}{dx^2})}]^2+ [\frac{(\frac{dy}{dx})^2+1}{\frac{d^2y}{dx^2}}]^2=r^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-229a46abad08a4e8243a8cce5155f2f9_l3.png)
Put (dy/dx) = y’ and d2y/dx2 = y”
y’2(1 + y’2)2 + (1 + y’2)2 = r2y”2
Question 9. Find the differential equation of all the circles which pass through the origin and whose centres lie on-axis.
Solution:
Equation of the circle is (x – a)2 + (y – b)2 = r2
Here, a and b are the centre of the circle.
(x – a)2 + (y – b)2 = r2 -(1)
When the centre lies on the y-axis, so a = 0
x2 + (y – b)2 = r2 -(2)
So, when the circle is passing through origin, so the equation is
02 + b2 = r2 -(3)
x2 + (y – b)2 = r2
On squaring both side, we have
x2 + y2 – 2yr + r2 = r2 -(Since r2 = b2)
2yr = x2 + y2
r = (x2 + y2)(2y)
On differentiating the equation(1) w.r.t x, we get
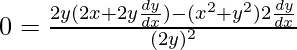
0 = 4xy + 4y2(dy/dx) – 2x2(dy/dx) – 2y2(dy/dx)
0 = y2(dy/dx) – x2(dy/dx) + 2xy
(x2 – y2)(dy/dx) = 2xy
Question 10. Find the differential equation of all the circles which pass through the origin and whose centres lie on the x-axis.
Solution:
Equation of the circle is (x – a)2 + (y – b)2 = r2
Here, a and b are the centre of the circle.
When the centre lies on the x-axis, so b = 0
(x – a)2 + y2 = r2 -(1)
When the circle is passing through origin, so the equation is
a2 + 02 = r2 -(2)
(x – a)2 + y2 = r2
On squaring both side, we get,
x2 – 2ax + a2 + y2 = r2
x2 + y2 – 2xr + r2 = r2 -(Since r2 = a2)
2xr = x2 + y2
r = (x2 + y2)(2x) -(3)
On differentiating the equation w.r.t x, we get
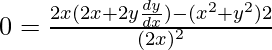
0 = 2x2 + 2xy(dy/dx) – x2 – y2
(x2 – y2) + 2xy(dy/dx) = 0
Share your thoughts in the comments
Please Login to comment...