Class 12 RD Sharma Solutions – Chapter 20 Definite Integrals – Exercise 20.5 | Set 2
Last Updated :
20 May, 2021
Evaluate the following definite integrals as limits of sums:
Question 12. 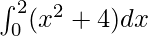
Solution:
We have,
I =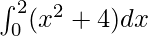
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =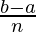
Here a = 0, b = 2 and f(x) = x2 + 4.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4+(h^2+4)+((2h)^2+4)+...+(((n-1)h)^2+4)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4854187f947d025e336959bbabce1b97_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4n+h^2(1^2+2^2+3^2+...+(n-1)^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6325c74d15e8b5db06c00ca6073a0165_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4n+h^2(1^2+2^2+3^2+...+(n-1)^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6325c74d15e8b5db06c00ca6073a0165_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4n+h^2(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ef05e11cfac780a4cdfae373eed5f079_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[4n+\frac{4}{n^2}(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-82a7b07c57f97193fd54c50a1b71e690_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[8+\frac{4n^3}{3n^3}(1-\frac{1}{n})(1-\frac{2}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8783724a658ab8f1497b8b3221cdf110_l3.png)
= 8 +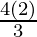
= 8 +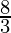
=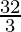
Therefore, the value of as limit of sum is
as limit of sum is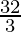 .
.
Question 13. 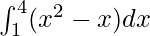
Solution:
We have,
I =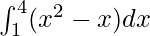
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =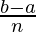
Here a = 1, b = 4 and f(x) = x2 − x.
=> h = 3/n
=> nh = 3
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ff4359373787dc7ac96481b49136a0c_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[(1^2-1)+[(1+h)^2-(1+h)]+[(1+2h)^2-(1+2h)]+...+[(1+(n-1)h)^2-(1+(n-1)h)]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1e3690295a3b0a31befcdb59e31857e0_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[0+[h+h^2]+[2h+(2h)^2]+...+[(n-1)h+((n-1)h)^2]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3555dfc841cedd0a110065a367e61e02_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[h(1+2+3+...+(n-1))+h^2(1^2+2^2+3^2+...+(n-1)^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b05b1590d1e5f1fbdd99a71a5f57da10_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[h(\frac{n(n-1)}{2})+h^2(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d4db8c16ae61d1186981ec46143c26b2_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{3}{n}[\frac{3}{n}(\frac{n(n-1)}{2})+\frac{9}{n^2}(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6a36388b63df7e340e3da596007b4bee_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[\frac{9n^2}{2n^2}(1-\frac{1}{n})+\frac{3n^3}{2n^3}(1-\frac{1}{n})(1-\frac{2}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c36eac81ce2e07650db4408a6ca5e682_l3.png)
=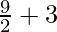
=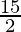
Therefore, the value of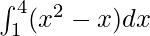 as limit of sum is
as limit of sum is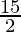 .
.
Question 14. 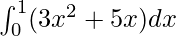
Solution:
We have,
I =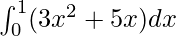
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =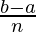
Here a = 0, b = 1 and f(x) = 3x2 + 5x.
=> h = 1/n
=> nh = 1
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[0+[3h^2+5h]+[3(2h)^2+5(2h)]+...+[3((n-1)h)^2+5((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-08927160f7a9cf65a6f6694e55917dc7_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[3h^2(1^2+2^2+3^2+...+(n-1)^2)+5h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1df00a0036d4b64055a3f35eb58c1b76_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[3h^2(\frac{n(n-1)(2n-1)}{6})+5h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6e9756ffb7d98db3e158c352e69560df_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{1}{n}[\frac{3}{n^2}(\frac{n(n-1)(2n-1)}{6})+\frac{5}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8285e6ab27ef9036862db3213afbf2ad_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[\frac{n^3}{2n^3}(1-\frac{1}{n})(2-\frac{1}{n})+\frac{5n^2}{2n^2}(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b6cf3a9643171f0281cdf114caf486ee_l3.png)
= 1 +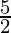
=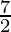
Therefore, the value of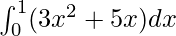 as limit of sum is
as limit of sum is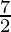 .
.
Question 15. 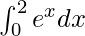
Solution:
We have,
I =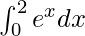
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =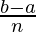
Here a = 0, b = 2 and f(x) = ex.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[1+e^h+e^{2h}+...+e^{(n-1)h}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-230a1cc8cedc2fb93226d688082a12a6_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[\frac{(e^h)^n-1}{e^h-1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-518deb898ad8ea8aa6ebc051c160d886_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[\frac{e^{nh}-1}{e^h-1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ecb2b3f1e56c6135391b24155922def3_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[\frac{e^{2}-1}{e^h-1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b9e77f8ed298687c0969f5107c6c97a1_l3.png)
=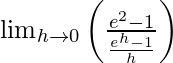
= e2 − 1
Therefore, the value of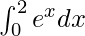 as limit of sum is e2 − 1.
as limit of sum is e2 − 1.
Question 16. 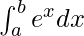
Solution:
We have,
I =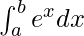
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =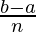
Here a = a, b = b and f(x) = ex.
=> h =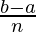
=> nh = b − a
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2f8339cb419850b9c59d654fd4923fae_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[e^a+e^{a+h}+e^{a+2h}+...+e^{a+(n-1)h}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c40ffcaae58f9d9396548c36af1dbd23_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}he^a[1+e^{h}+e^{2h}+...+e^{(n-1)h}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-60f790f404b578c91a6dad884facb65d_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}he^a[\frac{(e^h)^n-1}{e^h-1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-27182e29fa5ec176b4b17742582ac180_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}he^a[\frac{e^{nh}-1}{e^h-1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c8571a3703214a6db85f27f965939a27_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}he^a[\frac{e^{b-a}-1}{e^h-1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c3b4b3967a4fca804477c831df9cee1_l3.png)
=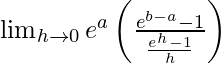
= ea (eb-a −1)
= eb − ea
Therefore, the value of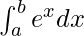 as limit of sum is eb − ea.
as limit of sum is eb − ea.
Question 17. 
Solution:
We have,
I =
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =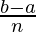
Here a = a, b = b and f(x) = cos x.
=> h =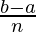
=> nh = b − a
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2f8339cb419850b9c59d654fd4923fae_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[cosa+cos(a+h)+cos(a+2h)+...+cos(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bb46e8db51c6b2cc56e43b587b7f05eb_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h\left[\frac{cos(a+(n-1)\frac{h}{2})sin\frac{nh}{2}}{sin\frac{h}{2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-97d8cd802b4ac7eba0c5435afc1d502a_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h\left[\frac{cos(a+\frac{nh}{2}-\frac{h}{2})sin\frac{nh}{2}}{sin\frac{h}{2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d27c10a6455b75cc0a5c6d421a12a926_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h\left[\frac{cos(a+\frac{b-a}{2}-\frac{h}{2})sin\frac{b-a}{2}}{sin\frac{h}{2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e5cb495fde7a8e4f2315ddeaf14cffd3_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}\left[\frac{\frac{h}{2}}{sin\frac{h}{2}}×2cos(a+\frac{b-a}{2}-\frac{h}{2})(sin\frac{b-a}{2})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-489ea99010938cf1743ec5c6887a5a02_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}\left[2cos(a+\frac{b-a}{2})sin(\frac{b-a}{2})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-31ff6aab316441871474be6e1a89bfca_l3.png)
=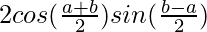
= sin b − sin a
Therefore, the value of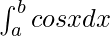 as limit of sum is sin b − sin a.
as limit of sum is sin b − sin a.
Question 18. 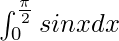
Solution:
We have,
I =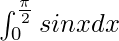
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =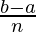
Here a = 0, b = and f(x) = sin x.
and f(x) = sin x.
=> h =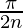
=> nh =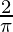
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[sin0+sinh+sin2h+...+sin(n-1)h]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b6df5fbe2a60c4ea16dcb6c469b5dec1_l3.png)
=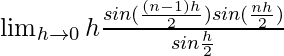
=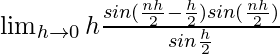
=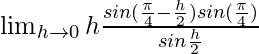
=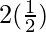
= 1
Therefore, the value of as limit of sum is 1.
as limit of sum is 1.
Question 19. 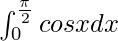
Solution:
We have,
I =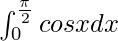
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =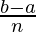
Here a = 0, b = and f(x) = cos x.
and f(x) = cos x.
=> h =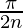
=> nh =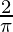
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[cos0+cosh+cos2h+...+cos(n-1)h]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f0621f3f94fccbc52afebd275c253000_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[\frac{cos(\frac{nh}{2}-\frac{h}{2})cos\frac{nh}{2}}{cos\frac{h}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-769ba01a9ad5781fae8b451600415d09_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[\frac{cos(\frac{\pi}{4}-\frac{h}{2})cos\frac{\pi}{4}}{cos\frac{h}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9991b755f5ad8fe07dc283d1d78e5533_l3.png)
=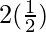
= 1
Therefore, the value of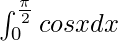 as limit of sum is 1.
as limit of sum is 1.
Question 20. 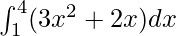
Solution:
We have,
I =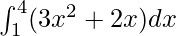
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =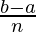
Here a =1, b = 4 and f(x) = 3x2 + 2x.
=> h = 3/n
=> nh = 3
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec2ad0db14527d4a0cb53e8f6d8833ff_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[(3+2)+[3(1+h)^2+2(1+h)]+[3(1+2h)^2+2(1+2h)]+...+[3(1+(n-1)h)^2+2(1+(n-1)h)]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-321049dff30ceda10ead89382552cc43_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[5n+8h(1+2+3...+(n-1))+3h^2(1^2+2^2+3^2+...+(n-1)^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a9533055685902efc4cebe08cdb9dfb_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[5n+8h(\frac{n(n-1)}{2})+3h^2(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-81b708eff4358830d25d76ab97d8e075_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{3}{n}[5n+\frac{24}{n}(\frac{n(n-1)}{2})+\frac{27}{n^2}(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e454f8b1fd6ed6fffb49f7ecdd5899d9_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[15+\frac{36n^2}{n^2}(1-\frac{1}{n})+\frac{27n^3}{2n^3}(1-\frac{1}{n})(2-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c82f4b78f02f626de7c67d713d17bdc7_l3.png)
= 15 + 36 + 27
= 78
Therefore, the value of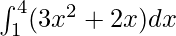 as limit of sum is 78.
as limit of sum is 78.
Question 21. 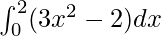
Solution:
We have,
I =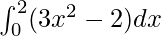
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =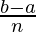
Here a =0, b = 2 and f(x) = 3x2 − 2.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[-2+[3h^2-2]+[3(2h)^2-2]+...+[3((n-1)h)^2-2]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1b30094bd18ae7ce0c5d2a778f2e838e_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[-2n+3h^2(1^2+2^2+3^2+...+(n-1)^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ff1880c6571bbc6b023c1fc2449f5d76_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[-2n+3h^2(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ac9c8f4a33487112a6aeda7dd34283b_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[-2n+\frac{12}{n^2}(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aa78947e17fd07bdee862c210b78b9fe_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[-4+\frac{4n^3}{n^3}(1-\frac{1}{n})(1-\frac{2}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c8d8a8bce4dbb4bc71c2ec511a578bb7_l3.png)
= −4 + 8
= 4
Therefore, the value of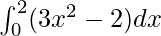 as limit of sum is 4.
as limit of sum is 4.
Question 22. 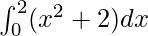
Solution:
We have,
I =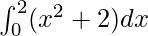
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =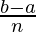
Here a =0, b = 2 and f(x) = x2 + 2.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[2+(h^2+2)+[((2h)^2+2)]+...+[((n-1)h)^2+2]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d7faa9a1ff28bd18f3fc25577e4cf7c6_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[2n+h^2(1^2+2^2+3^2+...+(n-1)^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fb42d28200bffaef6d3f32edc37e02d1_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[2n+h^2(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-63f8c859527e8f782099b1d704c8fb63_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[2+\frac{4}{n^2}(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-68a882d011f367178c087dbc0e38d8a2_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[4+\frac{4n^3}{n^3}(1-\frac{1}{n})(1-\frac{2}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-68b9a50842aa72aa49cf768ad921c630_l3.png)
= 4 +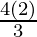
= 4 +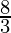
=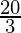
Therefore, the value of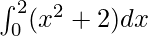 as limit of sum is
as limit of sum is .
.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...