Class 12 RD Sharma Solutions – Chapter 23 Algebra of Vectors – Exercise 23.5
Last Updated :
18 Mar, 2021
Question 1. If the position vector of a point (-4,-3) be 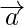 , find
, find 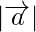 .
.
Solution:
We have,
![Rendered by QuickLaTeX.com \overrightarrow{a} = -4\hat i - 3\hat j \\|\overrightarrow{a}| = \sqrt[]{(-4)^2+ (-3)^2} \\ = \sqrt[]{16+9} \\ = \sqrt[]{25} \\= 5 \\|\overrightarrow{a}| = 5](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-77aba2bfd31d2156b1b8f1b26dda4a40_l3.png)
Question 2. If the position vector 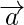 of a point (12,n) is such that
of a point (12,n) is such that 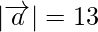 , find the value(s).
, find the value(s).
Solution:
We have,
![Rendered by QuickLaTeX.com \overrightarrow{a} = 12\hat i + n \hat j \\ |\overrightarrow{a}| = \sqrt[]{12^2 + n^2} \\ 13 = \sqrt[]{144 + n^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9f61693cf554f5e955cac011d991fb45_l3.png)
On squaring both sides,
![Rendered by QuickLaTeX.com (13)^2 = (\sqrt[]{144 + n^2})^2 \\169 = 144 + n^2 \\n^2 = 169 - 144 \\n^2 = 25 \\n^2 = \pm \sqrt[]{25} \\n = \pm 5](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c89701bda81788c9e282fe8ac731c7b3_l3.png)
Question 3. Find a vector of magnitude 4 units which is parallel to the vector ![Rendered by QuickLaTeX.com \sqrt[]{3} \hat i + \hat{j}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a97850b84826eb14a2e57cb1eb52e9cd_l3.png) .
.
Solution:
Given,

Let  is a vector parallel to
is a vector parallel to 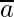 Therefore,
Therefore,
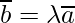 for any scalar
for any scalar
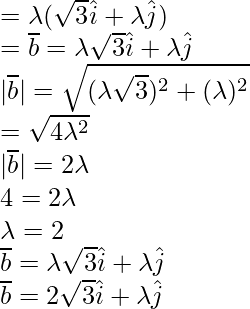
Question 4. Express 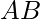 in terms of unit vectors (i)A = (4,-1),B = (1,3) (ii)A = (-6,3) , B = (-2,-5)
in terms of unit vectors (i)A = (4,-1),B = (1,3) (ii)A = (-6,3) , B = (-2,-5)
Solution:
(i) We have,
A = (4,-1)
B = (1,3)
Position Vector of A = 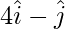 Position Vector of B =
Position Vector of B = 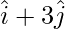 Now,
Now,
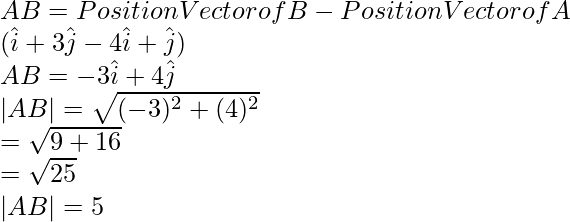 Therefore,
Therefore,
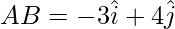 (ii) We have,
A = (-6,3)
B = (-2,-5)
Position Vector of A =
(ii) We have,
A = (-6,3)
B = (-2,-5)
Position Vector of A = 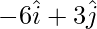 Position Vector of B =
Position Vector of B = 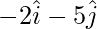 Now,
Now,
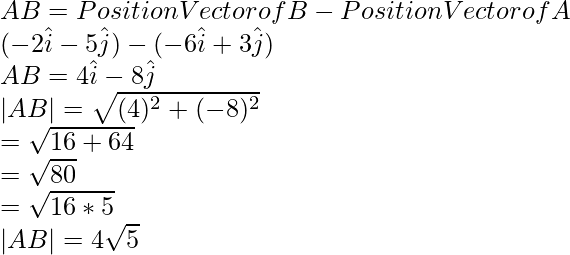 Therefore,
Therefore,
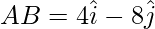
Question 5. Find the coordinates of the tip of the position vector which is equivalent to 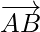 , where the coordinates of A and B are (-1,3) and (-2,1)
, where the coordinates of A and B are (-1,3) and (-2,1)
Solution:
We have,
A = (-1,3)
B = (-2,1)
Now,
Position Vector of 
Position Vector of 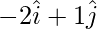
Therefore,
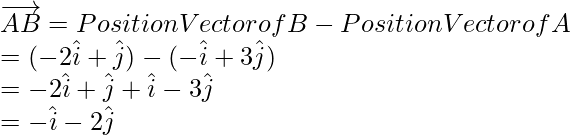
Coordinate of the position vector 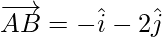
Question 6. ABCD is a parallelogram. If the coordinates of A,B,C are (-2,-1), (3,0),(1,-2) respectively, find the coordinates of D.
Solution:
Here, A = (-2,-1)
B = (3,0)
C = (1,-2)
Let us assume D be (x , y).
Computing Position Vector of AB, we have,
= Position Vector of B – Position Vector of A
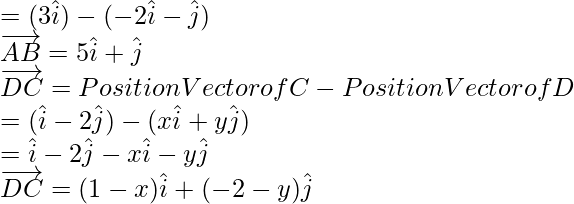
Comparing LHS and RHS of both,
5 = 1-x
x = -4
And,
1 = -2-y
y = -3
So, coordinates of D = (-4,-3).
Question 7. If the position vectors of the points A(3,4), B(5,-6) and C(4,-1) are 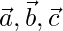 respectively, compute the value of
respectively, compute the value of 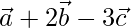 .
.
Solution:
Computing the position vectors of all the points we have,
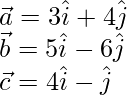
Now,
Computing the final value after substituting the values,
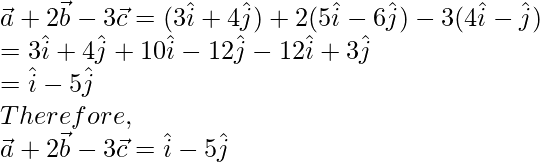
Question 8. If 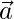 be the position vector whose tip is (-5,3), find the coordinates of a point B such that
be the position vector whose tip is (-5,3), find the coordinates of a point B such that 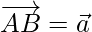 , the coordinates of A being (-4,1).
, the coordinates of A being (-4,1).
Solution:
Given,
Coordinate of A = (4,-1)
Position vector of A =  Position vector of
Position vector of 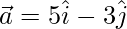 Let coordinate of point B = (x, y)
Position vector of B =
Let coordinate of point B = (x, y)
Position vector of B = 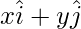 Given that,
Given that, 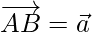 Position vector of B – Position vector of A = \vec{a}
Position vector of B – Position vector of A = \vec{a}
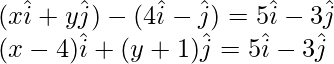 Comparing the coefficients of LHS and RHS
x – y = 5
x = 9
Also,
y + 1 = 3
y = -1
So, coordinate of B = (9,-4)
Comparing the coefficients of LHS and RHS
x – y = 5
x = 9
Also,
y + 1 = 3
y = -1
So, coordinate of B = (9,-4)
Question 9. Show that the points 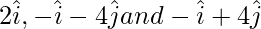 form an isosceles triangle.
form an isosceles triangle.
Solution:
![Rendered by QuickLaTeX.com |\overrightarrow{AB}| = 5 units \\ |\overrightarrow{BC}| = \sqrt[]{8^2} \\ |\overrightarrow{BC}| = 8 units \\ |\overrightarrow{AC}| = \sqrt[]{(-3)^2 + (8)^2} \\ = \sqrt[]{9+16} \\ = \sqrt[]{25} \\Here, \\|\overrightarrow{AB}| = |\overrightarrow{AC}|](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c9e9c94ef1a72498797e90693c8f5a11_l3.png)
So, the two sides AB and AC of the triangle ABC are equal.
Therefore, ABC is an isosceles triangle.
Question 10. Find a unit vector parallel to the vector  .
.
Solution:
We have,
Let 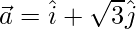
Suppose  is any vector parallel to
is any vector parallel to 
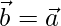 , where λ is any scalar.
, where λ is any scalar.
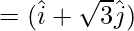
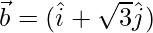
Unit vector of
![Rendered by QuickLaTeX.com \vec{b}= \frac{\vec{b}}{|\vec{b}|} \\ \hat{b} = \frac{\hat i + \sqrt[]{3} \hat j}{2} \\ \hat{b} = \frac{1}{2}(\hat i + \sqrt[]{3} \hat j)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3fb617eacbca6e8d31a760e6770a92a_l3.png) Therefore,
Therefore,
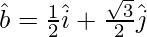
Question 11. Find the components along the coordinate axes of the position vector of each of the following points :
(i) P(3,2)
(ii) Q(-5,1)
(iii) R(-11,-9)
(iv) S(4,-3)
Solution:
(i) Given, P = (3,2)
Position vector of P = 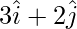
Component of P along x-axis = 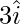
Component of P along y-axis = 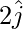
(ii) Given, Q = (-5,1)
Position vector of Q = 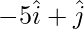
Component of Q along x-axis = 
Component of Q along y-axis =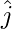
(iii) Given, R = (-11,-9)
Position vector of R =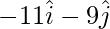
Component of R along x-axis =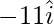
Component of R along y-axis = 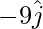
(iv) Given, S = (4,-3)
Position vector of S =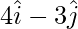
Component of S along x-axis =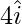
Component of S along y-axis = 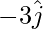
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...