Question 21: Maximize Z = 3x + 3y, if possible,
Subject to the constraints
x − y ≤ 1
x + y ≥ 3
x, y ≥ 0
Solution:
Convert the given in equations into equations, we will get the following equations:
x − y = 1, x + y = 3, x = 0 and y = 0
The area shown by x − y ≤ 1:
The line x − y = 1 coincide the coordinate axes at A(1, 0) and B(0, −1) respectively.
After connecting these points we will get the line x − y = 1.
Thus,
(0,0) assure the in equation x + y ≤ 8.
Thus,
The area in xy plane which have the origin shown the solution set of the in equation x − y ≤ 1.
The area shown by x + y ≥ 3:
The line x + y = 3 coincide the coordinate axes at C(3, 0) and D(0, 3) respectively.
After connecting these points we will get the line x + y = 3.
Thus,
(0,0) assure the in equation x + y ≥ 3.
Thus,
The area in xy plane which does not have the origin show the solution set of the in equation x + y ≥ 3.
The area shown by x ≥ 0 and y ≥ 0:
Hence,
All the points in the first quadrant assure these in equations. Thus, the first quadrant is the area shown by the in equations
x ≥ 0 and y ≥ 0.
The suitable area determined by the system of constraints x − y ≤ 1, x + y ≥ 3, x ≥ 0 and y ≥ 0 are as follows.

The suitable area is unbounded.
We will get the maximum value at infinity.
Hence,
Maximum value will be infinity i.e. the solution is unbounded.
Question 22. Show the solution zone of the following inequalities on a graph paper:
5x + y ≥ 10
x + y ≥ 6
x + 4y ≥ 12
x ≥ 0,
y ≥ 0
Find x and y for which 3x + 2y is minimum subject to these inequalities. Use a graphical method.
Solution:
Convert the given in equations into equations, we will get the following equations:
5x + y = 10, x +y = 6, x + 4y = 12, x = 0 and y = 0
The area shown by 5x + y ≥ 10:
The line 5x + y = 10 coincide the coordinate axes at A(2, 0) and B(0, 10) respectively.
After connecting these points we will get the line 5x + y = 10.
Thus,
(0,0) does not assure the in equation 5x + y ≥ 10.
Thus,
The area in xy plane which does not have the origin shows the solution set of the in equation 5x + y ≥ 10.
The area shown by x +y ≥ 6:
The line x +y = 6 coincide the coordinate axes at C(6,0) and D(0, 6) respectively.
After connecting these points we will get the line 2x +3y = 30.
Thus,
(0,0) does not assure the in equation x +y ≥ 6.
Thus,
The area which does not have the origin shows the solution set of the in equation 2x +3y ≥ 30.
The area shown by x + 4y ≥ 12
The line x + 4y = 12 coincide the coordinate axes at E(12, 0) and F(0, 3) respectively.
After connecting these points we will get the line x + 4y = 12.
Thus,
(0,0) does not assure the in equation x + 4y ≥ 12.
Thus,
The area which does not have the origin shows the solution set of the in equation x + 4y ≥ 12.
The area shown by x ≥ 0 and y ≥ 0:
Hence,
All the points in the first quadrant assure these in equations. Thus, the first quadrant is the area shown by the inequations
x ≥ 0, and y ≥ 0.
The suitable area determined by the system of constraints 5x + y ≥ 10, x +y ≥ 6,x + 4y ≥ 12, x ≥ 0, and y ≥ 0, are as follows.

The corner points of the suitable area are B(0, 10), G(1,5), H(4,2) and E(12,0).
The values of Z at these corner points are as follows.
Corner point
| Z = 3x + 2y
|
B(0, 10)
| 3 × 0 + 3 × 10 = 30
|
G(1,5)
| 3 × 1 + 2 × 5 = 13
|
H(4,2)
| 3 × 4 + 2 × 2 = 16
|
E(12,0)
| 3 × 12 + 2 × 0 = 36
|
Hence,
The minimum value of Z is 13 at the point G(1,5).
Therefore,
x = 1 and y = 5 is the best solution of the given LPP.
Therefore, the best value of Z is 13.
Question 23: Find the maximum and minimum value of 2x + y subject to the constraints:
x + 3y ≥ 6,
x − 3y ≤ 3,
3x + 4y ≤ 24,
− 3x + 2y ≤ 6,
5x + y ≥ 5,
x, y ≥ 0.
Solution:
Convert the given in equations into equations, we will get the following equations:
x + y = 4, x + y = 3, x − 2y = 2, x = 0 and y = 0.
The line x + 3y = 6 coincide the coordinate axis at A(6, 0)A6, 0 and B(0, 2).
Connect these points to get the line x + 3y = 6.
Thus,
(0, 0) does not assure the in equation x + 3y ≥ 6. Thus, the area in xy-plane that does not have the origin represents the
solution set of the given equation.
The line x − 3y = 3 coincide the coordinate axis at C(3, 0) and D(0, −1).
Connect these points to get the line x − 3y = 3.
Thus,
(0, 0) assure the in equation x − 3y ≤ 3. Thus, the area in xy-plane that have the origin represents the solution set of the given
equation.
The line 3x + 4y = 24 meets the coordinate axis at E(8, 0) and F(0, 6). Join these points to get the line 3x + 4y = 24.
Thus,
(0, 0) assure the in equation 3x + 4y ≤ 24. Thus, the area in xy-plane that have the origin shows the solution set of the given
equation.
The line −3x + 2y = 6 coincide the coordinate axis at G(−2, 0) and H(0, 3).
Connect these points to get the line −3x + 2y = 6.
Thus, (0, 0) assure the in equation −3x + 2y ≤ 6.
Thus,
The area in xy-plane that have the origin represents the solution set of the given equation.
The line 5x + y = 5 coincide the coordinate axis at I(1, 0)I1, 0 and J(0, 5).
Connect these points to get the line 5x + y = 5.
Thus,
(0, 0) does not assure the in equation 5x + y ≥ 5. Thus, the area in xy-plane that does not have the origin have the
solution set of the given equation.
The area shown by x ≥ 0 and y ≥ 0:
Hence,
All the points in the first quadrant assure these inequations. Thus, the first quadrant is the area shown by the in equations.
These lines are drawn using a satisfactory scale.

The corner points of the suitable area
are P 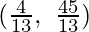 , K
, K 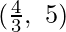 , L
, L 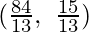 , M
, M 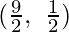 ,
,
N 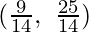
The values of Z at these corner points are as follows.
Corner point
| Z = 2x + y
|
P 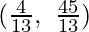
| 2 × 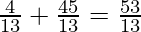
|
K 
| 2 × 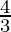 + 5 = + 5 = 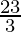
|
L 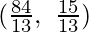
| 2 × 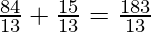
|
M 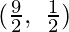
| 2 × 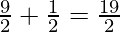
|
N 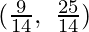
| 2 × 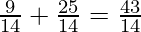
|
Here, we can see that the minimum value of the objective function Z is 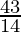 which is at N
which is at N 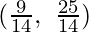
and maximum value of the objective function is 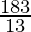 which is at L
which is at L 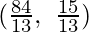 .
.
Question 24: Find the minimum value of 3x + 5y subject to the constraints
− 2x + y ≤ 4,
x + y ≥ 3,
x − 2y ≤ 2,
x, y ≥ 0.
Solution:
Convert the given in equations into equations, we will get the following equations:
−2x + y = 4, x + y = 3, x − 2y = 2, x = 0 and y = 0.
The line −2x + y = 4 coincide the coordinate axis at A(−2, 0)A-2, 0 and B(0, 4).
Connect these points to obtain the line −2x + y = 4.
Thus, (0, 0) assure the in equation −2x + y ≤ 4. So, the area in xy-plane that have the origin represents the solution set of the
given equation.
The line x + y = 3 coincide the coordinate axis at C(3, 0) and D(0, 3).
Connect these points to get the line x + y = 3.
Thus,
(0, 0) does not assure the in equation x + y ≥ 3. Thus, the area in xy-plane that does not have the origin shows the solution set
of the given equation.
The line x − 2y = 2 coincide the coordinate axis at E(2, 0) and F(0, −1).
Connect these points to get the line x − 2y = 2.
Thus,
(0, 0) assure the in equation x − 2y ≤ 2. Thus, the area in xy-plane that have the origin represents the solution set of the given
equation.
The area shown by x ≥ 0 and y ≥ 0:
Hence,
All the points in the first quadrant assure these in equations. Thus, the first quadrant is the area shown by the in equations.
These lines are drawn using a satisfactory scale.

The corner points of the suitable area are B(0, 4), D(0, 3) and G 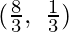 .
.
The values of Z at these corner points are as follows.
Corner point
| Z = 3x + 5y
|
B(0, 4)
| 3 × 0+ 5 × 4 = 20
|
D(0, 3)
| 3 × 0+ 5 × 3 = 15
|
G 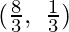
| 3 × 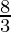 + 5 × + 5 × 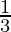 = = 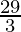
|
Here we can see that the minimum value of the objective function Z is 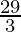 which is at G
which is at G 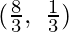 .
.
Therefore,
The best value of Z is 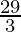 .
.
Question 25: Solved the following linear programming problem graphically:
Maximize Z = 60x + 15y
Subject to constraints
x + y ≤ 50
3x + y ≤ 90
x, y≥0
Solution:
Here we have to maximize Z = 60x + 15y
Convert the given in equations into equations, we get the following equations:
x + y = 50, 3x + y = 90, x = 0 and y = 0
The area shown by x + y ≤ 50:
The line x + y = 50 coincide the coordinate axes at A(50,0) and B(0,50) respectively.
After connecting these points we will get line 3x + 5y = 15.
Thus,
(0,0) assure the in equation x + y ≤ 50. Thus, the area having the origin shows the solution set of the in equation x + y ≤ 50.
The area shown by 3x + y ≤ 90:
The line 3x + y = 90 coincide the coordinate axes at C(30, 0) and D(0, 90) respectively.
After connecting these points we will get the line 3x + y = 90.
Thus,
(0,0) assure the in equation 3x + y ≤ 90. Thus, the area having the origin shows the solution set of the in equation 3x + y ≤ 90.
The area shown by x ≥ 0 and y ≥ 0:
Hence,
All the points in the first quadrant assure these in equations. Thus, the first quadrant is the area shown by the in equations
x ≥ 0, and y ≥ 0.
The suitable area determined by the system of constraints, x + y ≤ 50, 3x + y ≤ 90, x ≥ 0, and y ≥ 0, are as follows.

The corner points of the suitable area are O(0, 0), C(30, 0), E(20, 30) and B(0, 50).
The values of Z at these corner points are as follows.
Corner point
| Z = 60x + 15y
|
O(0, 0)
| 60 × 0 + 15 × 0 = 0
|
C(30, 0)
| 60 × 30 + 15 × 0 = 1800
|
E(20, 30)E20, 30
| 60 × 20 + 15 × 30 =1650
|
B(0, 50)
| 60 × 0 + 15 × 50 = 750
|
Hence,
The maximum value of Z is 1800 at the point (30, 0) at the point 30, 0.
Therefore,
x = 30 and y = 0 is the best solution of the given LPP.
Therefore,
The best value of Z is 1800.
Question 26. Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below:
2x + 4y ≤ 8
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≥ 0 [CBSE 2015]
Solution:
Here,
Maximize Z = 2x + 5y subject to the constraints
2x + 4y ≤ 8
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≥ 0
After converting the in equations into equations, we will get the following equations of straight lines:
2x + 4y = 8, 3x + y = 6, x + y = 4
The line 2x + 4y = 8 coincide the coordinate axes at (4, 0) and (0, 2).
The line 3x + y = 6 coincide the coordinate axes at (2, 0) and (0, 6).
The line x + y = 4 coincide the coordinate axes at (4, 0) and (0, 4).
The suitable area determined by the given constraints can be diagrammatically shown as,

The coordinates of the corner points of the suitable area are O(0, 0), A(0, 2), B 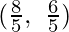 and C(2, 0).
and C(2, 0).
The value of the objective function at these points are given in the following table.
Corner Point
| Z = 2x + 5y
|
(0, 0)
| 2 × 0 + 5 × 0 = 0
|
(2, 0)
| 2 × 2 + 5 × 0 = 4
|
(0, 2)
| 2 × 0 + 5 × 2 = 10 → Maximum
|
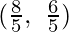
| 2×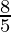 +5× +5×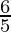 = =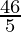
|
Therefore,
The maximum value of Z is 10 at x = 0, y = 2.
Question 27: Solve the following LPP graphically:
Maximize Z = 20x + x + 10y
Subject to the following constraints
x + 2y ≤ 28
3x + y ≤ 24
x ≥ 2
x,y ≥ 0
Solution:
Here given constraints are
x + 2y ≤ 28
3x + y ≤ 24
x ≥ 2
x, y ≥ 0
Converting the given in equations into equations,
we will get
x + 2y = 28, 3x + y = 24, x = 2, x = 0 and y = 0
These lines are drawn on the graph and the shaded region ABCD shown the suitable area of the given LPP.

It can be seen that the suitable area is bounded.
The coordinates of the corner points of the suitable area are A(2, 13), B(2, 0), C(4, 12) and D(8, 0).
The values of the objective function, Z at these corner points are given in the following table:
Corner Point
| Value of the Objective Function Z = 20x + 10y
|
A(2, 13)
| Z = 20 × 2 + 10 × 13 = 170
|
B(2, 0)
| Z = 20 × 2 + 10 × 0 = 40
|
C(8, 0)
| Z = 20 × 8 + 10 × 0 = 160
|
D(4, 12)
| Z = 20 × 4 + 10 × 12 = 200
|
As can be seen in the table, Z is maximum at x = 4 and y = 12 and the maximum value of Z is 200.
Therefore,
The maximum value of Z is 200.
Question 28: Solve the following linear programming problem graphically:
Minimize z= 6x + 3y
Subject to the constraints:
4x + y ≥ 80
x + 5y ≥ 115
3x + 2y ≤ 150
x ≥ 0, y ≥ 0
Solution:
Here the given constraints are
4x + y ≥ 80
x + 5y ≥ 115
3x + 2y ≤ 150
x, y ≥ 0
Converting the given in equations into equations,
We will get
4x + y = 80, x + 5y = 115, 3x + 2y = 150, x = 0 and y = 0
These lines are drawn on the graph and the shaded area ABC represents the suitable area of the given LPP.

It can be seen that the suitable area is bounded.
The coordinates of the corner points of the suitable are A(2, 72), B(15, 20) and C(40, 15).
The values of the objective function, Z at these corner points are given in the following table:
Corner Point
| Value of the Objective Function Z = 6x + 3y
|
A(2, 72)
| Z = 6 × 2 + 3 × 72 = 228
|
B(15, 20)
| Z = 6 × 15 + 3 × 20 = 150
|
C(40, 15)
| Z = 6 × 40 + 3 × 15 = 285
|
As seen in the table, Z is minimum at x = 15 and y = 20 and the minimum value of Z is 150.
Therefore,
The minimum value of Z is 150.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...