Class 12 RD Sharma Solutions – Chapter 16 Tangents and Normals – Exercise 16.1 | Set 1

Question 1. Find the slopes of the tangent and the normal to the following curves at the indicated points:

(i) y = √x³ at x = 4

(ii) y = √x at x = 9

(iii) y = x³ – x at x = 2

(iv) y = 2x² + 3 sin x at x = 0

(v) x = a(θ – sin θ), y = a(1 + cos θ) at θ = –π/2

(vi) x = a cos³ θ, y = a sin³ θ at θ = π/4

(vii) x = a(θ – sin θ), y = a(1 – cos θ) at θ = π/2

(viii) y = (sin 2x + cot x + 2)² at x = π/2

(ix) x² + 3y + y² = 5 at (1, 1)

(x) xy = 6 at (1, 6)

Solution:

We know that the slope of the tangent of a curve is given by dy/dx.

And slope of the normal = –1/slope of tangent = –1/(dy/dx).

(i) y = √x³ at x = 4

Differentiating y = √x³ with respect to x, we get,

Slope of tangent = 3x^1/2/2

At x = 4, slope of tangent becomes,

Slope of tangent = 3(4)^1/2/2 = 3(2)/2 = 3

And slope of normal at x = 4 is –1/3.

(ii) y = √x at x = 9

Differentiating y = √x with respect to x, we get,

Slope of tangent = x^–1/2/2

At x = 9, slope of tangent becomes,

Slope of tangent = 9^–1/2/2 = 1/[(3)(2)] = 1/6

And slope of normal at x = 9 is –6.

(iii) y = x³ – x at x = 2

Differentiating y = x³ – x with respect to x, we get,

Slope of tangent = 3x² – 1

At x = 2, slope of tangent becomes,

Slope of tangent = 3(2)² – 1 = 3(4) – 1 = 11

And slope of normal at x = 2 is –1/11.

(iv) y = 2x² + 3 sin x at x = 0

Differentiating y = 2x² + 3 sin x with respect to x, we get,

Slope of tangent = 4x + 3 cos x

At x = 0, slope of tangent becomes,

Slope of tangent = 4(0) + 3 cos 0 = 3.

And slope of normal at x = 0 is –1/3.

(v) x = a (θ – sin θ), y = a (1 + cos θ) at θ = –π/2

Differentiating x = a (θ – sin θ) with respect to θ, we get,

=> dx/dθ = a (1 – cos θ) . . . . (1)

Differentiating y = a (1 + cos θ) with respect to θ, we get,

=> dy/dθ = a (–sin θ) . . . . (2)

Dividing (2) by (1), we get,

dy/dx = Slope of tangent = –sin θ/(1 – cos θ)

At θ = –π/2, slope of tangent becomes,

Slope of tangent = –sin (–π/2)/(1 – cos (–π/2))

= 1/(1–0)

= 1

And slope of normal at θ = –π/2 is –1.

(vi) x = a cos³ θ, y = a sin³ θ at θ = π/4

Differentiating x = a cos³ θ with respect to θ, we get,

=> dx/dθ = a [(3cos² θ) (–sin θ)]

= –3a cos² θ sin θ . . . . (1)

Differentiating y = a sin³ θ with respect to θ, we get,

=> dy/dθ = a [(3sin² θ) (cos θ)]

= 3a sin² θ cos θ . . . . (2)

Dividing (2) by (1), we get,

dy/dx = Slope of tangent =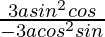= – tan θ

At θ = π/4, slope of tangent becomes,

Slope of tangent = – tan (π/4)

= −1

And slope of normal at θ = π/4 is 1.

(vii) x = a (θ – sin θ), y = a (1 – cos θ) at θ = π/2

Differentiating x = a (θ – sin θ) with respect to θ, we get,

=> dx/dθ = a (1 – cos θ) . . . . (1)

Differentiating y = a (1 – cos θ) with respect to θ, we get,

=> dy/dθ = a (sin θ) . . . . (2)

Dividing (2) by (1), we get,

dy/dx = Slope of tangent = sin θ/(1−cosθ)

= – tan θ

At θ = π/2, slope of tangent becomes,

Slope of tangent = sin π/2/(1−cos π/2)

= 1/(1−0)

= 1

And slope of normal at θ = π/2 is −1.

(viii) y = (sin 2x + cot x + 2)² at x = π/2

Differentiating y = (sin 2x + cot x + 2)² with respect to x, we get,

Slope of tangent = 2 (sin 2x + cot x + 2) (2 cos 2x – cosec² x)

At x = π/2, slope of tangent becomes,

Slope of tangent = 2 (sin 2(π/2) + cot π/2 + 2) (2 cos 2(π/2) – cosec² (π/2))

= 2 (0 + 0 + 2) (–2 – 1)

= –12

And slope of normal at x = π/2 is 1/12.

(ix) x² + 3y + y² = 5 at (1, 1)

Differentiating x² + 3y + y² = 5 with respect to x, we get,

=> 2x + 3 (dy/dx) + 2y (dy/dx) = 0

=> 2x + dy/dx (2y+3) = 0

=> Slope of tangent = dy/dx = –2x/(2y+3)

At x = 1 and y = 1, slope of tangent becomes,

Slope of tangent = –2(1)/[2(1)+3] = –2/5

And slope of normal at (1, 1) is 5/2.

(x) xy = 6 at (1, 6)

Differentiating xy = 6 with respect to x, we get,

=> x (dy/dx) + y = 0

=> Slope of tangent = dy/dx = –y/x

At x = 1 and y = 6, slope of tangent becomes,

Slope of tangent = –6/1 = –6

And slope of normal at (1, 6) is 1/6.

Question 2. Find the values of a and b if the slope of the tangent to the curve xy + ax + by = 2 at (1, 1) is 2.

Solution:

We know that the slope of the tangent of a curve is given by dy/dx.

Differentiating xy + ax + by = 2 with respect to x, we get

=> x (dy/dx) + y + a + b (dy/dx) = 2

=> dy/dx = −(a+y)/(x+b)

As we are given dy/dx = 2, we get,

=> −(a+y)/(x+b) = 2

Now at x = 1 and y = 1, we get,

=> −(a+1)/(1+b) = 2

=> −a − 1 = 2 + 2b

=> a + 2b = –3 . . . . (1)

Now the point (1, 1) also lies on the curve, so we have,

=> 1 × 1 + a × 1 + b × 1 = 2

=> 1 + a + b = 2

=> a + b = 1 . . . . (2)

Subtracting (1) from (2), we get,

=> –b = 1+3

=> b = –4

Putting b = –4 in (1), we get,

=> a = 1+4 = 5

Therefore, the value of a is 5 and b is –4.

Question 3. If the tangent to the curve y = x³ + ax + b at (1, –6) is parallel to the line x – y + 5 = 0, find a and b.

Solution:

We know that the slope of the tangent of a curve is given by dy/dx.

Differentiating y = x³ + ax + b with respect to x, we get

=> dy/dx = 3x² + a

Now at x = 1 and y = –6, we get,

=> dy/dx = 3(1)² + a

=> dy/dx = 3 + a . . . . (1)

Now this curve is parallel to the line x – y + 5 = 0.

=> y = x + 5

Therefore slope of the line is 1. So, the slope of the curve will also be 1 as slope of parallel lines are equal. So, from (1), we get,

=> dy/dx = 1 . . . . (2)

From (1) and (2), we get,

=> a + 3 = 1

=> a = –2 . . . . (3)

Now at x = 1 and y = –6, our curve y = x³ + ax + b becomes,

=> –6 = 1 + a + b

=> a + b = –7

Using (3), we get,

=> b = –7 – (–2)

=> b = –5

Therefore, the value of a is –2 and b is –5.

Question 4. Find a point on the curve y = x³ – 3x where the tangent is parallel to the chord joining (1, – 2) and (2, 2).

Solution:

We are given the coordinates of the chord (1, – 2) and (2, 2).

Therefore, slope of the chord =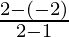= 4

Given curve is y = x³ – 3x. We know that the slope of the tangent of a curve is given by dy/dx.

=> dy/dx = 3x² – 3

As the tangent is parallel to the chord, its slope must be equal to 4.

=> 3x² – 3 = 4

=> 3x² = 7

=> x =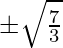

Putting value of x in the curve y = x³ – 3x, we get

=> y = x (x² – 3)

=> y =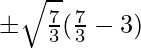

=> y =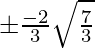

Therefore, the required point is.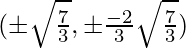

Question 5. Find a point on the curve y = x³ – 2x² – 2x at which the tangent lines are parallel to the line y = 2x – 3.

Solution:

Given curve is y = x³ – 2x² – 2x. We know that the slope of the tangent of a curve is given by dy/dx.

=> dy/dx = 3x² – 4x – 2 . . . . (1)

Now this curve is parallel to the line y = 2x – 3 whose slope is 2. So, the slope of the curve will also be 2. So, from (1), we get,

=> 3x² – 4x – 2 = 2

=> 3x² – 6x + 2x – 4 = 0

=> 3x (x – 2) + 2 (x – 2) = 0

=> (x – 2) (3x + 2) = 0

=> x = 2 or x = –2/3

If x = 2, we get

y = (2)³ – 2 × (2)² – 2 × (2)

= 8 – 8 – 4

= – 4

And if x = –2/3, we get,

y = (–2/3)³ – 2 × (–2/3)² – 2 × (–2/3)

=

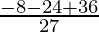
= 4/27

Therefore, (2, –4) and (–2/3, 4/27) are the required points.

Question 6. Find a point on the curve y² = 2x³ at which the slope of the tangent is 3.

Solution:

Given curve is y² = 2x³. We know that the slope of the tangent of a curve is given by dy/dx.

=> 2y dy/dx = 6x²

=> dy/dx = 3x²/y . . . . (1)

As it is given that the slope of tangent is 3, we get,

=> 3x²/y = 3

=> 3x² = 3y

=> x² = y

Putting this in the curve y² = 2x³, we get,

=> (x²)² = 2x³

=> x⁴ − 2x³ = 0

=> x³ (x − 2) = 0

=> x = 0 or x = 2

If x = 0, we get, y = 0. Putting these values in (1), we get dy/dx = 0, which is not possible as the given value of slope is 3.

And if x =2, we get y = 4.

Therefore, the required point is (2, 4).

Question 7. Find a point on the curve xy + 4 = 0 at which the tangents are inclined at an angle of 45^o with the x–axis.

Solution:

Given curve is xy + 4 = 0. We know that the slope of the tangent of a curve is given by dy/dx.

=> x (dy/dx) + y = 0

=> dy/dx = −y/x . . . . (1)

We are given that the tangent is inclined at an angle of 45^o with the x–axis. So slope of the tangent is,

dy/dx = tan 45^o = 1.

So, (1) becomes,

=> −y/x = 1

=> y = −x

Putting this in the curve xy + 4 = 0 we get,

=> x(−x) + 4 = 0

=> x² = 4

=> x = ±2

When x = 2, y = −2.

And when x = −2, y = 2.

Therefore, the required points are (2, – 2) & (– 2, 2).

Question 8. Find a point on the curve y = x² where the slope of the tangent is equal to the x – coordinate of the point.

Solution:

Given curve is y = x². We know that the slope of the tangent of a curve is given by dy/dx.

=> dy/dx = 2x . . . . (1)

It is given that the slope of the tangent is equal to the x – coordinate of the point.

Therefore, dy/dx = x . . . . (2)

From (1) & (2), we get,

2x = x

=> x = 0

Putting this in the curve y = x², we get,

=> y = 0²

=> y = 0

Therefore, the required point is (0, 0).

Question 9. At what point on the circle x² + y² – 2x – 4y + 1 = 0, the tangent is parallel to x – axis.

Solution:

Given circle is x² + y² – 2x – 4y + 1 = 0. We know that the slope of the tangent of a curve is given by dy/dx.

=> 2x + 2y (dy/dx) – 2 – 4 (dy/dx) = 0

=> dy/dx = (1– x)/(y– 2)

As the tangent is parallel to x-axis, its slope is equal to 0.

So, (1– x)/(y– 2) = 0

=> x = 1

Putting x = 1 in the circle x² + y² – 2x – 4y + 1 = 0, we get,

=> 1 + y² – 2 – 4y +1 = 0

=> y² – 4y = 0

=> y (y – 4) = 0

=> y = 0 and y = 4

Therefore, the required points are (1, 0) and (1, 4).

Question 10. At what point of the curve y = x² does the tangent make an angle of 45^o with the x–axis?

Solution:

Given curve is y = x². We know that the slope of the tangent of a curve is given by dy/dx.

=> dy/dx = 2x . . . . (1)

We are given that the tangent is inclined at an angle of 45^o with the x–axis. So slope of the tangent is

Therefore, dy/dx = tan 45^o = 1 . . . . (2)

From (1) & (2), we get,

2x = 1

=> x = 1/2

Putting this in the curve y = x², we get,

=> y = (1/2)²

=> y = 1/4

Therefore, the required point is (1/2, 1/4).