Class 12 RD Sharma Solutions – Chapter 7 Adjoint and Inverse of a Matrix – Exercise 7.1 | Set 3
Last Updated :
28 Mar, 2021
Question 25. Show that the matrix A = 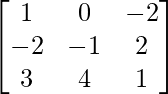 satisfies the equation A3 – A2 – 3A – I3 = 0. Hence, find A-1.
satisfies the equation A3 – A2 – 3A – I3 = 0. Hence, find A-1.
Solution:
Here, A = 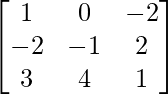
A2 = 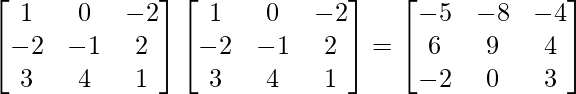
A3 = 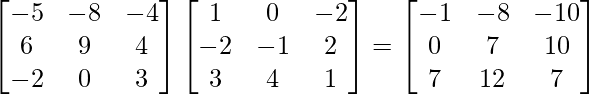
Now A3 – A2 – 3A – I3 = 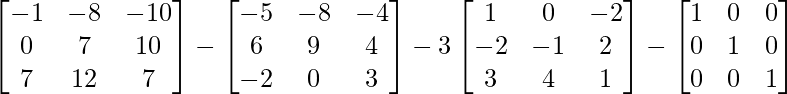
=
= 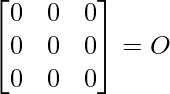
So, A3 – A2 – 3A – I3 = 0
⇒ A-1(AAA) – A-1(AA) – 3A-1A – A-1I = 0
⇒ A2 – A – 3I – A-1 = 0
⇒ A-1 = A2 – A – 3I
= 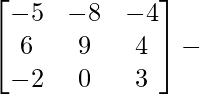
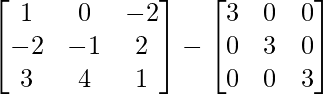
Therefore, A-1 =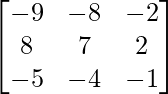
Question 26. If A = 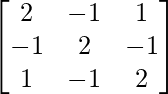 . Verify that A3 – 6A2 + 9A – 4I = O and hence find A-1.
. Verify that A3 – 6A2 + 9A – 4I = O and hence find A-1.
Solution:
Here, A = 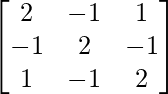
A2 = 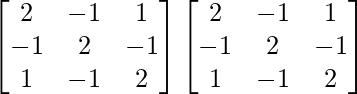
=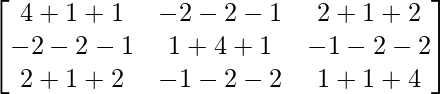
= 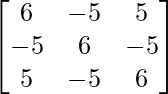
A3 = A2A = 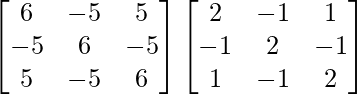
= 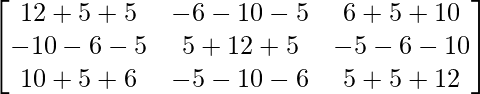
= 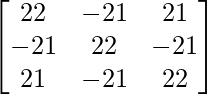
Now, A3 – 6A2 + 9A – 4I
= 
= 
= 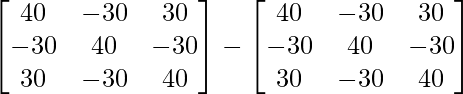
= 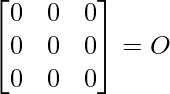
So, A3 – 6A2 + 9A – 4I = O
Multiplying both side by A-1
⇒ A-1(AAA) – 6A-1(AA) 9A-1A – 4A-1I = O
⇒ AAI – 6AI + 9I = 4A-1
⇒ 4A-1 = A2I – 6AI + 9I
=
=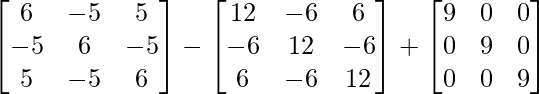
=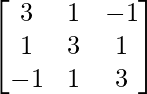
⇒ A-1 = 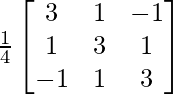
Question 27. If A =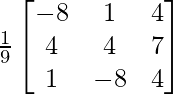 , prove that A-1 = AT.
, prove that A-1 = AT.
Solution:
Here, A = 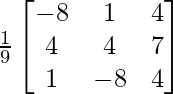
AT = 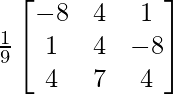
Now, Finding A-1
|A| = 1/9[-8(16 + 56) – 1(16 – 7) + 4(-32 – 4)]
= -81
Therefore, inverse of A exists
Cofactors of A are:
C11 = 72 C12 = -9 C13 = -36
C21 = -36 C22 = -36 C23 = -63
C31 = -9 C32 = 72 C33 = -36
adj A = 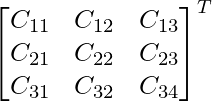
=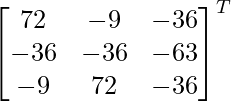
=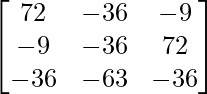
A-1 = 1/|A|. adj A
Hence, A-1 = 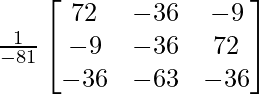
= 
= AT
Hence Proved
Question 28. If A = 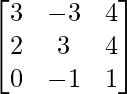 , show that A-1 = A3.
, show that A-1 = A3.
Solution:
Here, A = 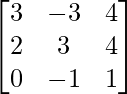
|A| = 3(-3 + 4) + 3(2 – 0) + 4(-2 – 0)
= 3 + 6 – 8
= 1
Therefore, inverse of A exists
Cofactors of A are:
C11 = 1 C12 = -2 C13 = -2
C21 = -1 C22 = 3 C23 = 3
C31 = 0 C32 = -4 C33 = -3
adj A =
A-1= 1/|A|. adj A
= 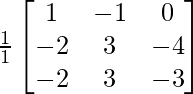
Now, A2 = 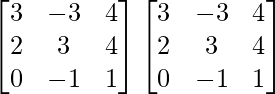
=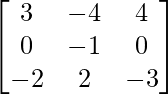
A3 = 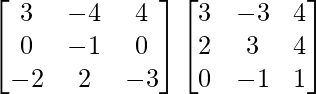
=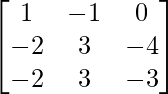
= A-1
Hence Proved
Question 29. If A =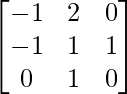 , show that A2 = A-1.
, show that A2 = A-1.
Solution:
Here, A = 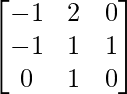
LHS = A2
= 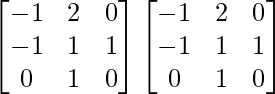
= 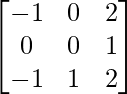
|A| = -1(1 – 0) – 2(-1 – 0) + 0
= 1
Therefore, inverse of A exists
Cofactors of A are:
C11 = -1 C12 = 0 C13 = -1
C21 = 0 C22 = 0 C23 = 1
C31 = 21 C32 = 1 C33 = 1
adj A = 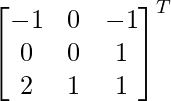
=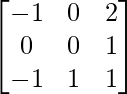
A-1 = 1/|A|. adj A
Hence, A-1 = 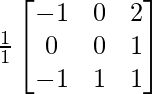
=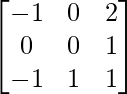
= A2
Hence Proved
Question 30. Solve the matrix equation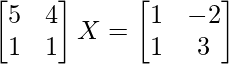 , where X is a 2×2 matrix.
, where X is a 2×2 matrix.
Solution:
We have, 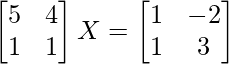
Let A =  and B =
and B = 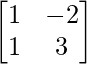
So. AX = B
⇒ X = A-1B
Now, |A| = 5 – 4 = 1
Co factors of A are:
C11 = 1 C12 = -1
C21 = -4 C22 = 5
adj A = 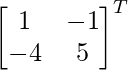
=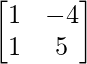
A-1 = 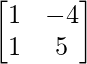
Therefore, X = 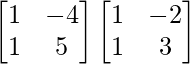
X = 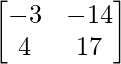
Question 31. Find the matrix X satisfying the matrix equation: X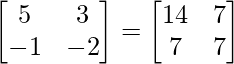 .
.
Solution:
We have, 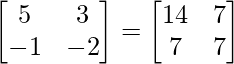
Let A =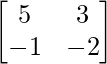 and B =
and B = 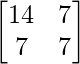
So, XA = B
XAA-1 = BA-1
XI = BA-1 ………..(i)
Now, |A| = -7
Co factors of A are:
C11 = -2 C12 = 1
C21 = -3 C22 = 5
adj A = 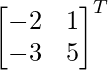
=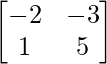
A-1 = 1/|A|.adj (A)
=
Therefore, X = 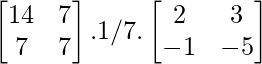
=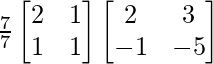
X = 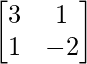
Question 32. Find the matrix X for which: 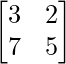 X
X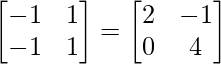
Solution:
Let, A = 
B = 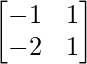
C = 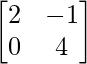
Then the given equation becomes
A × B = C
⇒ X = A-1CB-1
Now |A| = 35 -14 = 21
|B| = -1 + 2 = 1
A-1 = adj (A)/|A| = 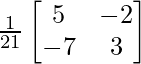
B-1 = adj (B)/|A| = 
X = A-1 CB-1 = 
= 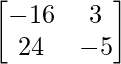
Question 33. Find the matrix X satisfying the equation: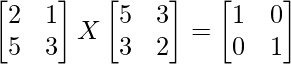
Solution:
Let A = B =
B = 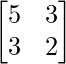
AXB = I
X = A-1B-1
|A| = 6 – 5 = 1
|B| = 10 – 9 = 1
A-1 = adj A /|A| = 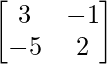
B-1 = adj B/|B| = 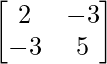
X = 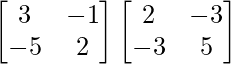
= 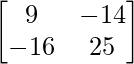
Question 34. If A = 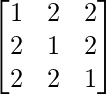 , Find A-1 and prove that A2 – 4A – 5I = O.
, Find A-1 and prove that A2 – 4A – 5I = O.
Solution:
Here, A = 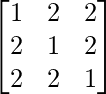
A2 = 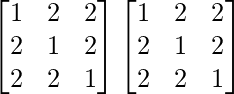
= 
Now, A2 + 4A – 5I
= 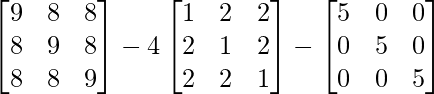
= 
Now, A2 – 4A – 5I = O
⇒ A-1AA – 4A-1A – 5A-1I = O
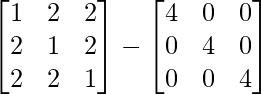
⇒ 5A-1 = [A – 4I]
= 
= 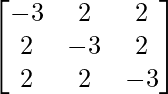
A-1 = 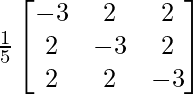
Question 35. If A is a square matrix of order n, prove that |A adj A| = |A|n.
Solution:
Given, |A adj A| = |A|n
Taking LHS = |A Adj A|
= |A| |Adj A|
= |A| |A|n-1
= |A|n-1+1
= |A|n = RHS
Hence Proved
Question 36. If A-1 = 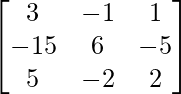 and B =
and B = 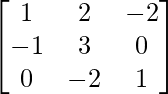 , find (AB)-1.
, find (AB)-1.
Solution:
Here, B = 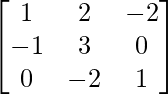
|B| = 1(3 – 0) – 2(-1 – 0) – 2(2 – 0)
= 3 + 2 – 4 = 1
Therefore, inverse of B exists
Cofactors of B are:
C11 = 3 C12 = 1 C13 = 2
C21 = 2 C22 = 1 C23 = 2
C31 = 6 C32 = 2 C33 = 5
adj A = 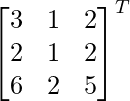
= 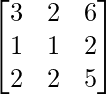
Therefore,
B-1 = 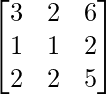
Hence, (AB)-1 = B-1A-1
= 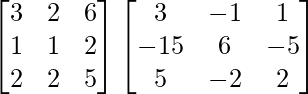
= 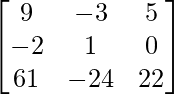
Question 37. If A = 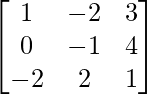 , find (AT)-1.
, find (AT)-1.
Solution:
Assuming B = AT = 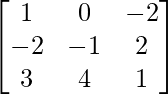
|B| = 1(-1 – 8) – 0 – 2(-8 + 3)
= -9 + 10 = 1
Therefore, inverse of B exists
Cofactors of B are:
C11 = -9 C12 = 8 C13 = -5
C21 = -8 C22 = 7 C23 = -4
C31 = -2 C32 = 2 C33 = -1
adj B = 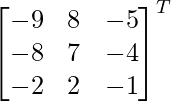
=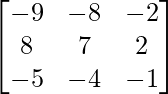
B-1 = 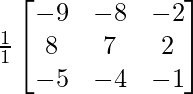
or (AT)-1 = 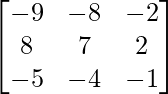
Question 38. Find the adjoint of the matrix A = 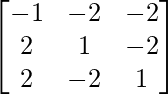 and hence show that A (adj A) = |A|I3.
and hence show that A (adj A) = |A|I3.
Solution:
Here, A = 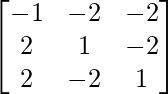
|A| = -1(1 – 4) – 2(2 + 4) – 2(-4 – 2)
= 3 + 12 + 12 = 27
Therefore, inverse of A exists
Cofactors of A are:
C11 = -3 C12 = -6 C13 = -6
C21 = 6 C22 = 3 C23 = -6
C31 = 6 C32 = -6 C33 = 3
adj A = 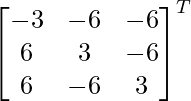
= 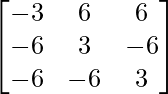
A (adj A) = 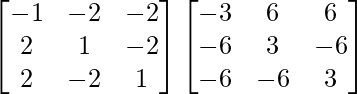
= 
or A (adj A) = 27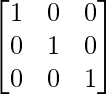
Hence, A (adj A) = |A|I3
Hence Proved
Question 39. If A = 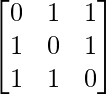 , A-1 and show that A-1 = 1/2(A2 – 3I).
, A-1 and show that A-1 = 1/2(A2 – 3I).
Solution:
Here, A = 
|A| = 0 – 1(0 – 1) + 1(1 – 0)
= 1 + 1 = 2
Therefore, inverse of A exists
Cofactors of A are:
C11 = -1 C12 = 1 C13 = 1
C21 = 1 C22 = -1 C23 = 1
C31 = 1 C32 = 1 C33 = -1
adj A = 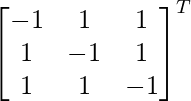
= 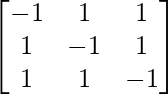
A-1 = 1/|A|. adj A
Hence, A-1 = 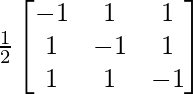
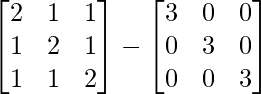
Now, A2 – 3I = 
=
=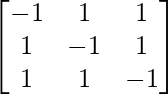
Hence, A-1 = 1/2(A2 – 3I)
Hence Proved
Share your thoughts in the comments
Please Login to comment...