Question 1. Find the area of the triangle with vertices at the points:
(i) (3, 8), (−4, 2) and (5, −1)
Solution:
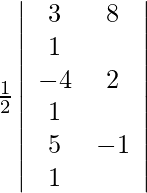
Given (3, 8), (−4, 2) and (5, −1) are the vertices of the triangle.
We know that, if vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by,
A = 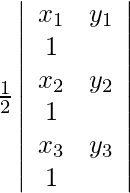
= 
= ![Rendered by QuickLaTeX.com \frac{1}{2}[3(2+1)-8(-4-5)+1(4-10)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-78dc308cc4c4b5192c20d7f9ff998a01_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}[9+72-6]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4483f643a989835323195af93eb52f1b_l3.png)
= 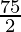
Therefore, area of the triangle is 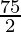 sq. units.
sq. units.
(ii) (2, 7), (1, 1) and (10, 8)
Solution:
Given (2, 7), (1, 1) and (10, 8) are the vertices of the triangle.
The area of the triangle is given by,
A = 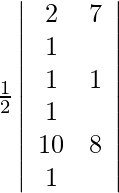
= ![Rendered by QuickLaTeX.com \frac{1}{2}[2(1-8)-7(1-10)+1(8-10)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b73ffcd6f0bcbd50e31c9990ab0a6226_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}[-14+63-2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-851908224594aa0371b4f294e1f559c2_l3.png)
= 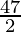
Therefore, area of the triangle is 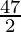 sq. units.
sq. units.
(iii) (−1, −8), (−2, −3) and (3, 2)
Solution:
Given (−1, −8), (−2, −3) and (3, 2) are the vertices of the triangle.
The area of the triangle is given by,
A = 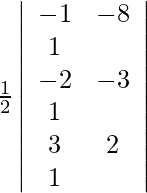
= 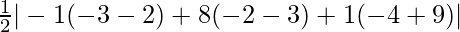
= 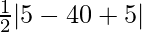
= 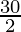
= 15
Therefore, area of the triangle is 15 sq. units.
(iv) (0, 0), (6, 0), (4, 3)
Solution:
Given (0, 0), (6, 0), (4, 3) are the vertices of the triangle.
The area of the triangle is given by,
A = 
= ![Rendered by QuickLaTeX.com \frac{1}{2}[0-0+1(18-0)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0e55172f9f6e2baca93052d2b3e167d1_l3.png)
= 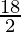
= 9
Therefore, area of the triangle is 9 sq. units.
Question 2. Using the determinants show that the following points are collinear:
(i) (5, 5), (−5, 1) and (10, 7)
Solution:
Given points are (5, 5), (−5, 1) and (10, 7).
For these points to be collinear, the area of the triangle they form must be zero. So, we get,
A = 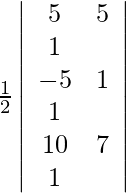
= ![Rendered by QuickLaTeX.com \frac{1}{2}[5(1-7)-5(-5-10)+1(-35-10)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9c4ee65abd01e0cf887b69562369e4c4_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}[-30+75-45]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c503325a82fa77cb73c78ac294740e15_l3.png)
= 0
As the area of the triangle is 0, the points are collinear.
Hence proved.
(ii) (1, −1), (2, 1) and (4, 5)
Solution:
Given points are (1, −1), (2, 1) and (10, 8).
For these points to be collinear, the area of the triangle they form must be zero. So, we get,
A = 
= ![Rendered by QuickLaTeX.com \frac{1}{2}[1(1-5)+1(2-4)+1(10-4)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-abc1567c0164b72b06619de252cc9c9f_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}[-4-2+6]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-846888f360882640ea5f81dbad48828c_l3.png)
= 0
As the area of the triangle is 0, the points are collinear.
Hence proved.
(iii) (3, −2), (8, 8) and (5, 2)
Solution:
Given points are (3, −2), (8, 8) and (5, 2).
For these points to be collinear, the area of the triangle they form must be zero. So, we get,
A = 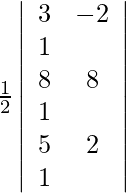
= ![Rendered by QuickLaTeX.com \frac{1}{2}[3(8-2)+2(8-5)+1(16-40)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-32da6c319538da887e67baf2a986c61d_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}[18+6-24]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a5f057cbd0121eab6171511f26a0e421_l3.png)
= 0
As the area of the triangle is 0, the points are collinear.
Hence proved.
(iv) (2, 3), (−1, −2) and (5, 8)
Solution:
Given points are (2, 3), (−1, −2) and (5, 8).
For these points to be collinear, the area of the triangle they form must be zero. So, we get,
A = 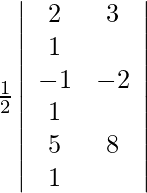
= ![Rendered by QuickLaTeX.com \frac{1}{2}[2(-2-8)-3(-1-5)+1(-8+10)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8fbeefc087cc271e521ced56e1e5529f_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}[-20+18+2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d67ed3722bc5168db2c4824ce56b08b6_l3.png)
= 0
As the area of the triangle is 0, the points are collinear.
Hence proved.
Question 3. If the points (a, 0), (0, b) and (1, 1) are collinear, prove that a + b = ab.
Solution:
Given points (a, 0), (0, b) and (1, 1) are collinear.
For these points to be collinear, the area of the triangle they form must be zero. So, we get,
=> 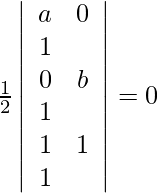
=> ![Rendered by QuickLaTeX.com \frac{1}{2}[a(b-1)-0+1(0-b)]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8d6686470d0934b76ba92c5a8e8bcf29_l3.png)
=> ab − a − b = 0
=> a + b = ab
Hence proved.
Question 4. Using the determinants prove that the points (a, b), (a’, b’), and (a – a’, b – b) are collinear if a b’ = a’ b.
Solution:
Given points are (a, b), (a’, b’) and (a – a’, b – b) and a b’ = a’ b.
For these points to be collinear, the area of the triangle they form must be zero. So, we get,
=> 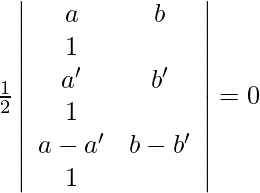
=> ![Rendered by QuickLaTeX.com \frac{1}{2}[a(b'-b+b')-b(a'-a+a')+1(a'b-a'b'-ab'+a'b')]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1363d05713aa09598931b584144a9581_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{1}{2}[ab'-ab+ab'-a'b+ab-a'b+a'b-ab')]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8c63d17105c272bbf90d74e8d1583649_l3.png)
=> a b’ − a’ b = 0
=> a b’ = a’ b
Hence proved.
Question 5. Find the value of λ so that the points (1, −5), (−4, 5), and (λ, 7) are collinear.
Solution:
Given points are (1, −5), (−4, 5) and (λ, 7).
For these points to be collinear, the area of the triangle they form must be zero. So, we get,
=> 
=> ![Rendered by QuickLaTeX.com \frac{1}{2}[1(5-7)+5(-4-λ)+1(-28-5λ)]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e822ee294f136f44966e637eaa4806c4_l3.png)
=> −2 − 20 − 5λ − 28 − 5λ = 0
=> 10λ = 50
=> λ = 5
Therefore, the value of λ is 5.
Question 6. Find the value of x if the area of ∆ is 35 square cms with vertices (x, 4), (2, −6), and (5, 4).
Solution:
Given points are (x, 4), (2, −6) and (5, 4).
We know that, if vertices of a triangle are (x1, y1), (x2, y2) and (x3, y3), then the area of the triangle is given by,
A = 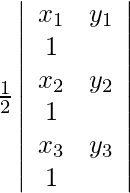
=> 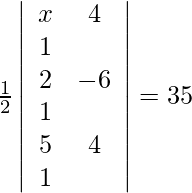
=> 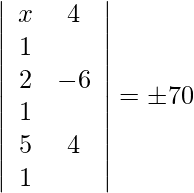
=> − 10x + 12 + 38 = ±70
=> – 10x + 50 = ±70
Taking positive sign, we get
=> – 10x + 50 = 70
=> 10x = – 20
=> x = – 2
Taking negative sign, we get
=> – 10x + 50 = – 70
=> 10x = 120
=> x = 12
Therefore, the value of x is 12 or –2.
Question 7. Using determinants, find the area of the triangle whose vertices are (1, 4), (2, 3), (–5, –3). Are the given points collinear?
Solution:
Given points are (1, 4), (2, 3), (–5, –3).
So, area = 
= 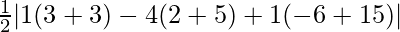
= 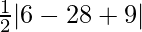
= 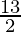
As the area of the triangle formed by these three points is not zero, the points are not collinear.
Question 8. Using determinants, find the area of the triangle with vertices (–3, 5), (3, –6), (7, 2).
Given points are (–3, 5), (3, –6), (7, 2).
So, area = 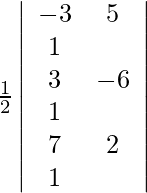
= 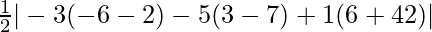
= 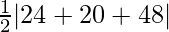
= 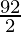
= 46
Therefore, the area of the triangle is 46 sq. units.
Question 9. Using determinants, find the value of k so that the points (k, 2–2k), (–k+1, 2k), (–4–k, 6–2k) may be collinear.
Solution:
Given points are (k, 2–2k), (–k+1, 2k), (–4–k, 6–2k). As the points are collinear, the area must be 0.
=> 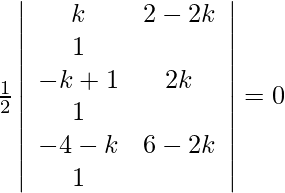
=> k(2k – 6 + 2k) – (2–2k) (–k + 1 + 4 + k) + [(1–k) (6–2k) – 2k (–4–k)] = 0
=> 8k2 + 4k – 4 = 0
=> 8k2 + 8k – 4k – 4 = 0
=> 8k (k+1) – 4 (k+1) = 0
=> 8k = 4 or k = –1
=> k = 1/2 or k = –1
Therefore, the value of k is 1/2 or –1.
Question 10. If the points (x, –2), (5, 2), (8, 8) are collinear, find x using determinants.
Solution:
Given points are (x, –2), (5, 2), (8, 8). As the points are collinear, the area must be 0.
=> 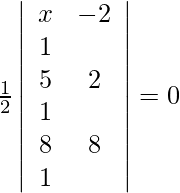
=> x(2 – 8) + 2(5 – 8) + 1(40–16) = 0
=> –6x – 6 + 24 = 0
=> 6x = 18
=> x = 3
Therefore, the value of x is 3.
Question 11. If the points (3, –2), (x, 2), (8, 8) are collinear, find x using determinants.
Solution:
Given points are (3, –2), (x, 2), (8, 8). As the points are collinear, the area must be 0.
=> 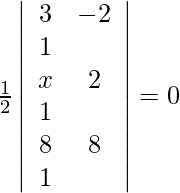
=> 3(2 – 8) + 2(x – 8) + 1(8x–16) = 0
=> –18 + 2x – 16 + 8x – 16 = 0
=> 10x = 50
=> x = 5
Therefore, the value of x is 5.
Question 12. Using determinants, find the equation of
(i) the line joining the points (1, 2) and (3, 6).
Solution:
Let (x, y), (1, 2), (3, 6) be the points on the line. As these points are collinear, we get,
=> 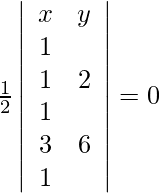
=> ![Rendered by QuickLaTeX.com \frac{1}{2}[x(2-6)-y(1-3)+1(6-6)]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-575f429b990502bf6b4002589f43d105_l3.png)
=> −4x + 2y = 0
=> 2x − y = 0
Therefore, the required equation is 2x − y = 0.
(ii) the line joining the points (3, 1) and (9, 3).
Solution:
Let (x, y), (3, 1), (9, 3) be the points on the line. As these points are collinear, we get,
=> 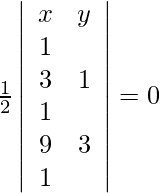
=> ![Rendered by QuickLaTeX.com \frac{1}{2}[x(1-3)-y(3-6)+1(9-9)]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-15783b75464003704db199eeae496669_l3.png)
=> −2x + 6y = 0
=> x − 3y = 0
Therefore, the required equation is x − 3y = 0.
Question 13. Find the values of k
(i) if area of triangle whose vertices are (k, 0) (4, 0) (0, 2) is 4 square units.
Solution:
Given points are (k, 0) (4, 0) (0, 2). According to the question, we have,
=> 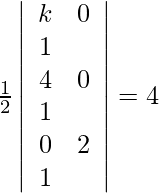
=> |k(0−2) − 0 + 1(8−0)| = 8
=> −2k + 8 = ±8
=> −2k + 8 = 8 or −2k + 8 = −8
=> k = 0 or k = 8
Therefore, the value of k is 0 or 8.
(ii) if area of triangle whose vertices are (−2, 0) (0, 4) (0, k) is 4 square units.
Solution:
Given points are (−2, 0) (0, 4) (0, k). According to the question, we have,
=> 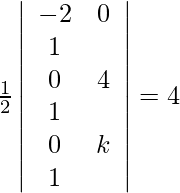
=> |−2(4−k) − 0 + 1(0)| = 8
=> −8 + 2k = ±8
=> −8 + 2k = 8 or −8 + 2k = −8
=> k = 8 or k = 0
Therefore, the value of k is 0 or 8.
Share your thoughts in the comments
Please Login to comment...