Solve the following differential equations:
Question 21. (1 – x2)dy + xydx = xy2dx
Solution:
We have,
(1 – x2)dy + xydx = xy2dx
(1 – x2)dy = xy2dx – xydx
(1 – x2)dy = xy(y – 1)dx
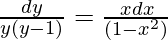
On integrating both sides,
![Rendered by QuickLaTeX.com ∫[\frac{1}{y-1}-\frac{1}{y}]dy=\frac{1}{2}∫\frac{2x}{1-x^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8be564dcf956e863f47f52d551e0b612_l3.png)
log(y – 1) – logy = -(1/2)log(1 – x2) + logc
log(y – 1) – logy + (1/2)log(1 – x2) = logc (Where ‘c’ is integration constant)
Question 22. tanydx + sec2ytanxdy = 0
Solution:
We have,
tanydx + sec2ytanxdy = 0
tanydx = -sec2ytanxdy
(sec2y/tany)dy = -dx/tanx
On integrating both sides,
∫(sec2y/tany)dy = -∫cotxdx
Let, tany = z
On differentiating both sides
sec2xdx = dz
∫(dz/z) = -∫cotxdx
log(z) = -log(sinx) + log(c)
On putting the value of z in above equation
log(tany) + log(sinx) = log(c)
log[(sinx)(tany)] = log(c)
sinx.tany = c (Where ‘c’ is integration constant)
Question 23. (1 + x)(1 + y2)dx + (1 + y)(1 + x2)dy = 0
Solution:
We have,
(1 + x)(1 + y2)dx + (1 + y)(1 +x2)dy = 0
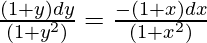
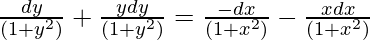
On integrating both sides,
tan-1(y) + (1/2)log(1 + y2) = -tan-1(x) – (1/2)log(1 + x2) + c
tan-1(y) + tan-1(x) + (1/2)log[(1 + y2)(1 + x2)] = c (Where ‘c’ is integration constant)
Question 24. tany(dy/dx) = sin(x + y) + sin(x – y)
Solution:
We have,
tany(dy/dx) = sin(x + y) + sin(x – y)
tany(dy/dx) = 2sin{(x + y + x – y)/2}cos{(x + y – x + y)/2}
tany(dy/dx) = 2sinxcosy
(tany/cosy)dy = 2sinxdx
On integrating both sides,
∫secytanydy = 2∫sinxdx
secy = -2cosx + c
secy + cosx = c (Where ‘c’ is integration constant)
Question 25. cosxcosy(dy/dx) = -sinxsiny
Solution:
We have,
cosxcosy(dy/dx) = -sinxsiny
(cosy/siny)dy = -(sinx/cosx)dx
cotydy = -tanxdx
On integrating both sides,
∫cotydy = -∫tanxdx
log(siny) = log(cosx) + logc
log(siny) = log(cosx.c)
siny = c.cosx (Where ‘c’ is integration constant)
Question 26. (dy/dx) + cosxsiny/cosy = 0
Solution:
We have,
(dy/dx) + cosxsiny/cosy = 0
(dy/dx) = -cosx.tany
dy/tany = -cosxdx
cotydy = -cosxdx
On integrating both sides,
∫cotydy = -∫cosxdx
log(cosy) = -sinx + c
log(cosy) + sinx = c (Where ‘c’ is integration constant)
Question 27. x√(1 – y2)(dx) + y√(1 – x2)dy = 0
Solution:
We have,
x√(1 – y2)(dx) + y√(1 – x2)dy = 0
x√(1 – y2)(dx) = -y√(1 – x2)dy
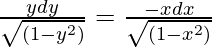
On integrating both sides,
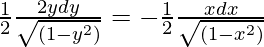
√(1 – y2) = -√(1 – x2) + c
√(1 – y2) + √(1 – x2) = c (Where ‘c’ is integration constant)
Question 28. y(1 + ex)dy =(y + 1)exdx
Solution:
We have,
y(1 + ex)dy =(y + 1)exdx
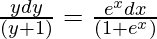

On integrating both sides,
∫[1 – 1/(y + 1)]dy = ∫exdx/(1 + ex)
y – log(y + 1) = log(1 + ex) + c (Where ‘c’ is integration constant)
Question 29. (y + xy)dx + (x – xy2)dy = 0
Solution:
We have,
(y + xy)dx + (x – xy2)dy = 0
y(1 + x)dx = -x(1 – y2)dy
[(1 – y2)/y]dy = -[(1 + x)/x]dx
On integrating both sides,
∫[(1 – y2)/y]dy = -∫[(1 + x)/x]dx
∫(dy/y) – ∫ydy = -∫dx/x – ∫dx
log(y) – (y2/2) = -log(x) – x + c
log(x) + x + log(y) – (y2/2) = c (Where ‘c’ is integration constant)
Question 30. (dy/dx) = 1 – x + y – xy
Solution:
We have,
(dy/dx) = 1 – x + y – xy
(dy/dx) = (1 – x) + y(1 – x)
(dy/dx) = (1 – x)(1 – y)
dy/(1 – y) = (1 – x)dx
On integrating both sides,
∫dy/(1 – y) = ∫(1 – x)dx
log(1 – y) = x – (x2/2) + c (Where ‘c’ is integration constant)
Question 31. (y2 + 1)dx – (x2 + 1)dy = 0
Solution:
We have,
(y2 + 1)dx – (x2 + 1)dy = 0
(y2 + 1)dx = (x2 + 1)dy
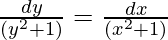
On integrating both sides,
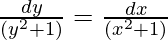
tan-1y = tan-1x + c (Where ‘c’ is integration constant)
Question 32. dy + (x + 1)(y + 1)dx = 0
Solution:
We have,
dy + (x + 1)(y + 1)dx = 0
dy/(y + 1) = -(x + 1)dx
On integrating both sides,
∫dy/(y + 1) = -∫(x + 1)dx
log(y + 1) = -(x2/2) – x + c
log(y + 1) + (x2/2) + x = c (Where ‘c’ is integration constant)
Question 33. (dy/dx) = (1 + x2)(1 + y2)
Solution:
We have,
(dy/dx) = (1 + x2)(1 + y2)
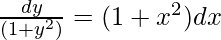
On integrating both sides,
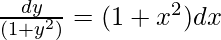
tan-1y = x + (x3/3) + c
tan-1y – x – (x3/3) = c (Where ‘c’ is integration constant)
Question 34. (x – 1)(dy/dx) = 2x3y
Solution:
We have,
(x – 1)(dy/dx) = 2x3y
dy/y = 2x3dx/(x – 1)
On integrating both sides,
∫dy/y = 2∫x3dx/(x – 1)
![Rendered by QuickLaTeX.com log(y)=2∫[x^2+x+1+\frac{1}{(x-1)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d12f9d14e7cca5215827d61b3079d8d8_l3.png)
log(y) = (2/3)(x3) + 2(x2/2) + 2x + 2log(x – 1) + log(c)
![Rendered by QuickLaTeX.com log(y)=loge^{[\frac{2}{3}x^3+x^2+2x]}+log(x-1)^2+logc](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c71e080ae4d620455fcdd742960b9571_l3.png)
y = c|x – 1|2e[(2/3)x3+x2+2x] (Where ‘c’ is integration constant)
Question 35. (dy/dx) = ex+y + e-x+y
Solution:
We have,
(dy/dx) = ex+y + e-x+y
(dy/dx) = ex.ey + e-x.ey
(dy/dx) = ey(ex + e-x)
dy/ey = (ex + e-x)dx
On integrating both sides,
∫e-ydy = ∫exdx + ∫e-xdx
-e-y = ex – e-x + c
e-x-e-y = ex + c (Where ‘c’ is integration constant)
Question 36. (dy/dx) = (cos2x – sin2x)cos2y
Solution:
We have,
(dy/dx) = (cos2x – sin2x)cos2y
dy/cos2y = (cos2x – sin2x)dx
sex2ydy = cos2xdx
On integrating both sides,
∫sex2ydy = ∫cos2xdx
tany = (sin2x/2) + c (Where ‘c’ is integration constant)
Question 37(i). (xy2 + 2x)(dx) + (x2y + 2y)dy = 0
Solution:
We have,
(xy2 + 2x)(dx) + (x2y + 2y)dy = 0
x(y2 + 2)(dx) = -y(x2 + 2)dy
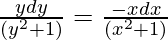
Multiplying both sides by 2,
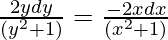
On integrating both sides,
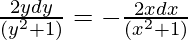
log(y2 + 1) = -log(x2 + 1) + log(c)
![Rendered by QuickLaTeX.com (y^2+1)=[\frac{1}{(x^2+1)}]c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0e675d13f7fb52ddd99893a16b0af9f_l3.png)
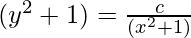 (Where ‘c’ is integration constant)
(Where ‘c’ is integration constant)
Question 37 (ii). cosecx logy(dy/dx) + x2y2 = 0
Solution:
We have,
cosecx logy(dy/dx) + x2y2 = 0
log(y)dy/y2 = -x2dx/cosecx
On integrating both sides,
∫[log(y)/y2]dy = -∫x2sinxdx
![Rendered by QuickLaTeX.com log(y)∫\frac{dy}{y^2}-∫[\frac{d(logy)}{dy}∫\frac{dy}{y^2}]dy=-[x^2∫sinxdx-∫(\frac{d(x^2)}{dx}∫sinxdx)dx]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8429ca3202497bcfd7254ec9d101f9c9_l3.png)
-log(y)/y + ∫dy/y2 = x2cosx – 2∫xcosxdx + c
-log(y)/y – 1/y = x2cosx – 2[x∫cosxdx – ∫{dx/dx∫cosxdx}dx] + c
-[{log(y) + 1}/y] = x2cosx – 2(xsinx – ∫sinxdx) + c
x2cosx + [{log(y) + 1}/y] – 2(xsinx + cosx) = c
Question 38 (i). xy(dy/dx) = 1 + x + y + xy
Solution:
We have,
xy(dy/dx) = 1 + x + y + xy
xy(dy/dx) = (1 + x) + y(1 + x)
xy(dy/dx) = (1 + x)(1 + y)
ydy/(1 + y) = [(1 + x)/x]dx
On integrating both sides,
∫ydy/(1 + y) = ∫[(1 + x)/x]dx
∫[1 – 1/(1 + y)]dy = ∫(dx/x) + ∫dx
y – log(1 + y) = log(x) + x + log(c)
y = log(x) + log(1 + y) + x + log(c)
y = log[cx(1 + y)] + x (Where ‘c’ is integration constant)
Question 38 (ii). y(1 – x2)(dy/dx) = x(1 + y2)
Solution:
We have,
y(1 – x2)(dy/dx) = x(1 + y2)
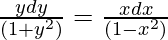
On integrating both sides,
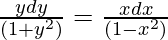
Multiplying both sides by 2,
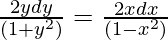
log(1 + y2) = -log(1 – x2) + log(c)
log[(1 + y2)(1 – x2)] = logc
(1 + y2)(1 – x2) = c (Where ‘c’ is integration constant)
Question 38 (iii). yex/ydx = (xex/y + y2)dy
Solution:
We have,
yex/ydx = (xex/y + y2)dy
yex/ydx – xex/ydy = y2dy
ex/y(ydx – xdy)/y2 = dy
ex/yd(x/y) = dy
On integrating both sides,
∫ex/yd(x/y) = ∫dy
ex/y = y + c (Where ‘c’ is integration constant)
Question 38 (iv). (1 + y2)tan-1xdx + 2y(1 + x2)dy = 0
Solution:
We have,
(1 + y2)tan-1xdx + 2y(1 + x2)dy = 0 -(i)
![Rendered by QuickLaTeX.com \frac{ydy}{(1+y^2)}=-[\frac{tan^{-1}x}{2(1+x^2)}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3072614a3875edf7e14e19c32ee5f2e6_l3.png)
On integrating both sides,
![Rendered by QuickLaTeX.com ∫\frac{ydy}{(1+y^2)}=-∫[\frac{tan^{-1}x}{2(1+x^2)}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-53dcb6e3df0bbf0f7e6184e4ec46da9b_l3.png) -(ii)
-(ii)
Let, I = ![Rendered by QuickLaTeX.com ∫[\frac{tan^{-1}x}{2(1+x^2)}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9d105c5b7621a90130e1c84fae366594_l3.png)
![Rendered by QuickLaTeX.com I=tan^{-1}x∫\frac{1}{2(x^2+1)}dx-∫[\frac{d}{dx}(tan^{-1}x)∫\frac{1}{2(x^2+1)}dx]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c429546839e0a7c19d5c0d9d60a55033_l3.png)

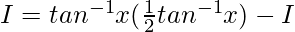
2I = (1/2)(tan-1x)2
I = (1/4)(tan-1x)2
From equation (ii)
(1/2)log(1 + y2) = -(1/4)(tan-1x)2 + c
log(1 + y2) + (1/2)(tan-1x)2 = c
Question 39. (dy/dx) = ytan2x, y(0) = 2
Solution:
We have,
(dy/dx) = ytan2x
(dy/y) = tan2xdx
On integrating both sides,
∫(dy/y) = ∫tan2xdx
log(y) = (1/2)log(sec2x) + log(c)
y = c(sec2x)1/2
Put x = 0, y = 2 in above equation
c = 2
y = 2(sec2x)1/2
Share your thoughts in the comments
Please Login to comment...