Class 12 RD Sharma Solutions – Chapter 20 Definite Integrals – Exercise 20.5 | Set 3
Last Updated :
20 May, 2021
Evaluate the following definite integrals as limits of sums:
Question 23. 
Solution:
We have,
I =
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =
Here a = 0, b = 4 and f(x) = x + e2x.
=> h = 4/n
=> nh = 4
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[1+[h+e^{2h}]+[2h+e^{4h}]+...+[(n-1)h+e^{2(n-1)h}]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-614bcfe6d9d5e4878f29b20beef2e2ed_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[h(1+2+3+...+(n-1))+(1+e^{2h}+e^{4h}+...e^{2(n-1)h})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-76721c33afd135a67bc054fdf2a329de_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[h(\frac{n(n-1)}{2})+(\frac{(e^{2h})^2-1}{e^{2h}-1})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5dab5858a7d4d25f2b6a6512725355b6_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[h(\frac{n(n-1)}{2})+(\frac{e^{2nh}-1}{e^{2h}-1})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9fa0638ac33622581b429cca3aa0131c_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h^2\left[(\frac{n(n-1)}{2})+\left(\frac{e^{8}-1}{2(\frac{e^{2h}-1}{h})}\right)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2cc996ca0ac8452a5ccb2ec2bf00e228_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[\frac{16}{n^2}(\frac{n(n-1)}{2})+(\frac{e^{8}-1}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-923d09b90e8a5b708d6384128806d4a1_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[\frac{8n^2}{n^2}(1-\frac{1}{n})+(\frac{e^{8}-1}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c9bec6ff3eb1d51606fd4e2e85fbadc_l3.png)
=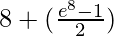
=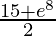
Therefore, the value of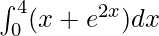 as limit of sum is
as limit of sum is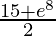 .
.
Question 24. 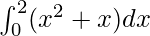
Solution:
We have,
I =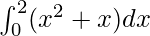
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =
Here a = 0, b = 2 and f(x) = x2 + x.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[0+(h^2+h)+[(2h)^2+2h]+...+[(n-1)h)^2+(n-1)h]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7843e18a1c003c88d9a919447056b57e_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[h^2(1^2+2^2+3^2+...(n-1)^2)+h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-da618b026d85a6234f43c304e253ddaa_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[h^2(\frac{n(n-1)(2n-1)}{6})+h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9f79b7c583b1d5c48e7fd8ead93357a4_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[\frac{4}{n^2}(\frac{n(n-1)(2n-1)}{6})+\frac{2}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-22ca24e8b453b7b4cc03f06991e0febe_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[\frac{4n^3}{n^3}(1-\frac{1}{n})(2-\frac{1}{n})+\frac{2n^2}{n^2}(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-12466034fb58cb890080d4e287f759ff_l3.png)
=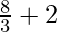
=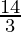
Therefore, the value of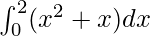 as limit of sum is
as limit of sum is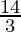 .
.
Question 25. 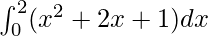
Solution:
We have,
I =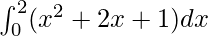
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =
Here a = 0, b = 2 and f(x) = x2 + 2x + 1.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[1+(h^2+2h+1)+[(2h)^2+2(2h)+1]+...[(n-1)^2+2(n-1)+1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9f1f2be175c5f3eebd901cb2af265977_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[n+h^2(1^2+2^2+3^2+...(n-1)^2)+2h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-07b4d5c5e0514c0bcd1571c950e01ceb_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[n+h^2(\frac{n(n-1)(2n-1)}{6})+2h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4dedb572d724a37dd5c4b876dec89354_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[n+\frac{4}{n^2}(\frac{n(n-1)(2n-1)}{6})+\frac{4}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e7f02ed8d42c47636387979a994b4784_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[2+\frac{4n^3}{n^3}(1-\frac{1}{n})(2-\frac{1}{n})+\frac{4n^2}{n^2}(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3fab220f5ad062a1889af073899e49e2_l3.png)
=
=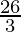
Therefore, the value of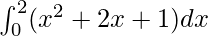 as limit of sum is
as limit of sum is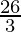 .
.
Question 26. 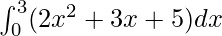
Solution:
We have,
I =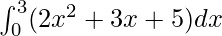
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =
Here a = 0, b = 3 and f(x) = 2x2 + 3x + 5.
=> h = 3/n
=> nh = 3
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[5+(2h^2+3h+5)+[2(2h)^2+3(2h)+5]+...+[2(n-1)^2h^2+3((n-1)h)+5]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bc414fed35c36dce2aac650d38f5c8db_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[5n+2h^2(1^2+2^2+3^2+...+(n-1)^2)+3h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d6b9564209444fe94239ea04818a8fae_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[5n+2h^2(\frac{n(n-1)(2n-1)}{6})+3h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cfc1d88b7026905e2e920702df647eee_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{3}{n}[5n+\frac{18}{n^2}(\frac{n(n-1)(2n-1)}{6})+\frac{9}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ba26bd92b37ebc246ae90bd634c85ef3_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[15+\frac{9n^3}{n^3}(1-\frac{1}{n})(2-\frac{1}{n})+\frac{27n^2}{2n^2}(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0c42d8e2b105d547aeda2e0f96523a5a_l3.png)
= 15 + 18 +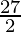
=
Therefore, the value of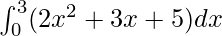 as limit of sum is
as limit of sum is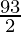 .
.
Question 27. 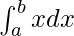
Solution:
We have,
I =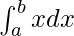
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =
Here a = a, b = b and f(x) = x.
=> h =
=> nh = b − a
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2f8339cb419850b9c59d654fd4923fae_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[a+(a+h)+(a+2h)+...+(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4842c91cf935e9ce7bc06e0384ac7231_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[na+h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f4750da499467c7717ef2cc67cfbfc0c_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[na+h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-10f0e9e7ac2df99dd552de753dd12f64_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{b-a}{n}[na+\frac{b-a}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0fa8c5810ee3fb1c8cf6fb40e8755c43_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}(b-a)[a+\frac{b-a}{n}(\frac{n-1}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5da22759df61711c8ad27f6ddd069bb3_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}(b-a)[a+(b-a)(\frac{1-\frac{1}{n}}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9542c568cb7381d41ce670abcbc77eeb_l3.png)
=![Rendered by QuickLaTeX.com (b-a)[a+\frac{b-a}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b674a0a99c596de26cdfb91d347c883b_l3.png)
=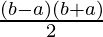
=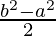
Therefore, the value of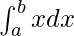 as limit of sum is
as limit of sum is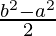 .
.
Question 28. 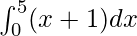
Solution:
We have,
I =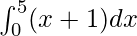
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =
Here a = 0, b = 5 and f(x) = x + 1.
=> h =5/n
=> nh = 5
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[1+(h+1)+(2h+1)+...+((n-1)h+1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a50a569f42b8f59dc7e36850a196d0d_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[n+h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ecfe821660fb52955685ce0b20947197_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[n+h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-46b0de65731191d37a398f3e3be4a384_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{5}{n}[n+\frac{5}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-17869b8c206d6bde178845223140547e_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[5+\frac{25n^2}{2n^2}(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-72e3ca686aaf4c0adbcbcf5db2b32559_l3.png)
= 5 +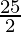
=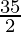
Therefore, the value of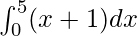 as limit of sum is
as limit of sum is .
.
Question 29. 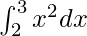
Solution:
We have,
I =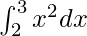
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =
Here a = 2, b = 3 and f(x) = x2.
=> h = 1/n
=> nh = 1
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(2)+f(2+h)+f(2+2h)+...+f(2+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc18938dd8a01b1c881a44f0feefe6cd_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4+(2+h)^2+(2+2h)^2+...+(2+(n-1)h)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-194e64a1a64f32a72d0e4c9ac8fd4284_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4+[2^2+2.h+h^2]+[2^2+2.2h+(2h)^2]+...]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3cd4047dcfadb3615fd4d9263f2d3327_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4n+h^2(1^2+2^2+...+(n-1)^2)+4h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b5a165e54fc66f1b5388f66ccdb6c5f5_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4n+h^2(\frac{n(n-1)(2n-1)}{6})+4h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-10b4c487c00685b741fd24c1767efabe_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{1}{n}[4n+\frac{1}{n^2}(\frac{n(n-1)(2n-1)}{6})+\frac{4}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f0fe0f0c77628bd97f7907de855a11e4_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[4+\frac{n^3}{6n^3}(1-\frac{1}{n})(2-\frac{1}{n})+\frac{2n^2}{n^2}(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4013e6e7c18ab8aa5d9f8b6332868b22_l3.png)
=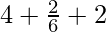
=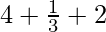
=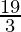
Therefore, the value of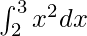 as limit of sum is
as limit of sum is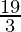 .
.
Question 30. 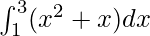
Solution:
We have,
I =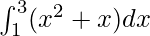
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =
Here a = 1, b = 3 and f(x) = x2 + x.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ff4359373787dc7ac96481b49136a0c_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[2+[(1+h)^2+(1+h)]+[(1+2h)^2+(1+2h)]+...]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-459c593264d24bc4fd12f2450b3c5d7f_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[2n+h^2(1^2+2^2+3^2+...+(n-1)^2)+3h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7cc1908e17df5108d06b8fafb174267a_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[2n+h^2(\frac{n(n-1)(2n-1)}{6})+3h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b0e6ff417ee2152a2d40aa762c852a5a_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[2n+\frac{4}{n^2}(\frac{n(n-1)(2n-1)}{6})+\frac{6}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-db1a5ea7d7c37c42043a5f257fc22746_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[4+\frac{4n^3}{3n^3}(1-\frac{1}{n})(2-\frac{1}{n})+\frac{6n^2}{n^2}(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9d99616733d5768a4871b2a4be1ac9a7_l3.png)
=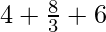
=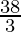
Therefore, the value of as limit of sum is
as limit of sum is .
.
Question 31. 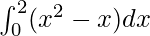
Solution:
We have,
I =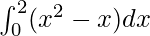
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =
Here a = 0, b = 2 and f(x) = x2 − x.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[0+[h^2-h]+[(2h)^2-2h]+...]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-56743dfb3e34346805bdf6d30f1742e8_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[h^2(1^2+2^2+...+(n-1)^2)-h(1+2+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2447e99d39e326ce9c3aaba902225da4_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[h^2(\frac{n(n-1)(2n-1)}{6})-h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3fe200c9ad1a0aeedf7d87b077d24ab9_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[\frac{4}{n^2}(\frac{n(n-1)(2n-1)}{6})-\frac{2}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1abeea216f2e8f963a684bf46517a292_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[\frac{4n^3}{3n^3}(1-\frac{1}{n})(2-\frac{1}{n})-\frac{2n^2}{n^2}(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-edbec34ca165a1b70826b5e994e99bab_l3.png)
=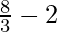
=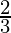
Therefore, the value of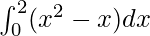 as limit of sum is
as limit of sum is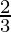 .
.
Question 32. 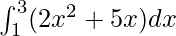
Solution:
We have,
I =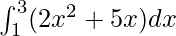
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =
Here a = 1, b = 3 and f(x) = 2x2 + 5x.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ff4359373787dc7ac96481b49136a0c_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[7+[2(1+h)^2+5(1+h)]+[2(1+2h)^2+5(1+2h)]+...]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-05d629a9740cc9c7f3c03558d3e10928_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[7n+9h(1+2+3+...+(n-1))+2h^2(1^2+2^2+3^2+...(n-1)^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-755112d1668794a783ad11de607bc7e2_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[7n+9h(\frac{n(n+1)}{2})+2h^2(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5ce2740ae9ef243202885199caa612bc_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[7n+\frac{18}{n}(\frac{n(n-1)}{2})+\frac{8}{n^2}(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3f3976e8b93579faa7bb3604388dff72_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[14+\frac{18n^2}{n^2}(1-\frac{1}{n})+\frac{8n^3}{3n^3}(1-\frac{1}{n})(2-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2df433cd8c3a2e6a42fb8e9ba72d18ad_l3.png)
= 14 + 18 +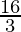
=
Therefore, the value of as limit of sum is
as limit of sum is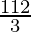 .
.
Question 33. 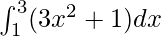
Solution:
We have,
I =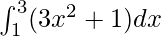
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e52175da43d6f708d8eb142f906f9d2d_l3.png) , where h =
, where h =
Here a = 1, b = 3 and f(x) = 3x2 + 1.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ff4359373787dc7ac96481b49136a0c_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4+[3(1+h)^2+1]+[3(1+2h)^2+1]+...]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5e557ba9027247429b297bdef941cc9b_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4n+6h(1+2+3+...(n-1))+3h^2(1^2+2^2+3^2+...(n-1)^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2f32f5005e46970dea89178e3b46863a_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4n+6h(\frac{n(n-1)}{2})+3h^2(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f6fd1568537a41b750a08eb88d081db5_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[4n+\frac{12}{n}(\frac{n(n-1)}{2})+\frac{12}{n^2}(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5b0ca2b17f3664ea328dc6d0339c6220_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[8+\frac{12n^2}{n^2}(1-\frac{1}{n})+\frac{4n^3}{n^3}(1-\frac{1}{n})(2-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-63f7803efa97ac6ae260cd6c254de58a_l3.png)
= 8 + 12 + 8
= 28
Therefore, the value of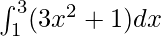 as limit of sum is 28.
as limit of sum is 28.
Share your thoughts in the comments
Please Login to comment...