Evaluate the following definite integrals:
Question 23. 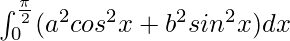
Solution:
We have,
I = 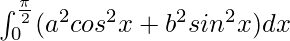
I = 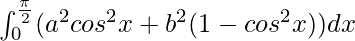
I = ![Rendered by QuickLaTeX.com \int_{0}^{\frac{\pi}{2}} [(a^2-b^2)cos^2x+b^2]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8b812aa75ecb672c36c4fc4b7a95a231_l3.png)
I = ![Rendered by QuickLaTeX.com \int_{0}^{\frac{\pi}{2}} [(a^2-b^2)(\frac{1+cos2x}{2})]dx+\int_{0}^{\frac{\pi}{2}}b^2dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b187b8105ee1f0f4df2c25d226fb98d4_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{a^2-b^2}{2}\int_{0}^{\frac{\pi}{2}} [(1+cos2x)]dx+\int_{0}^{\frac{\pi}{2}}b^2dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-45cb43f6960e5f64635379a23920c360_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{a^2-b^2}{2}\left[x+\frac{sin2x}{2}\right]_{0}^{\frac{\pi}{2}}+b^2\left[x\right]_{0}^{\frac{\pi}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f1b30129c0ef65fe8ea18d09e7c0ed98_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{a^2-b^2}{2}\left[\frac{\pi}{2}+sin\pi-0-0\right]+b^2\left[\frac{\pi}{2}-0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-69b737f978040d2fe8e2b0a96031d3b2_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{a^2-b^2}{2}\left[\frac{\pi}{2}\right]+b^2\left[\frac{\pi}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d30ed1dab72e607ad2f7b0779a190a9e_l3.png)
I = ![Rendered by QuickLaTeX.com (\frac{a^2-b^2}{2}+b^2)\left[\frac{\pi}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5afb68e9c52cf85f5f381a96a4062a8c_l3.png)
I = ![Rendered by QuickLaTeX.com (\frac{a^2-b^2+2b^2}{2})\left[\frac{\pi}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d43aa441327004745027d2a269665169_l3.png)
I = [(a2 + b2)/2][π/2]
I = π(a2 + b2)/4
Therefore, the value of 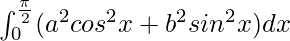 is π(a2 + b2)/4.
is π(a2 + b2)/4.
Question 24. 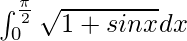
Solution:
We have,
I = 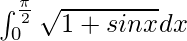
I = 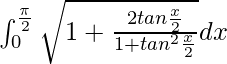
I = 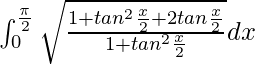
I = 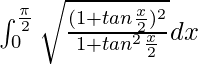
I = 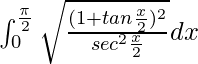
I = 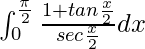
I = 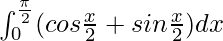
I = ![Rendered by QuickLaTeX.com \left[2sin\frac{x}{2}-2cos\frac{x}{2}\right]_{0}^{\frac{\pi}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6a86cc8fc389b7b7f2fcf1315091513d_l3.png)
I = 2[sinπ/4 – cosπ/4 – 0 + 1]
I = 2[1/√2 – 1/√2 – 0 + 1]
I = 2 (1)
I = 2
Therefore, the value of 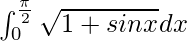 is 2.
is 2.
Question 25. 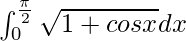
Solution:
We have,
I = 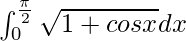
I = 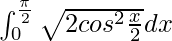
I = 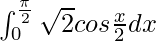
I = 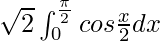
I = ![Rendered by QuickLaTeX.com \sqrt{2}\left[2sin\frac{x}{2}\right]_{0}^{\frac{\pi}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3b7115cfd818c1b2ad1603ebd8f670c_l3.png)
I = ![Rendered by QuickLaTeX.com 2\sqrt{2}\left[sin\frac{x}{2}\right]_{0}^{\frac{\pi}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fb71d25d6623b698467b41c1d54f4d03_l3.png)
I = 2√2[sinπ/4 – sin0]
I = 2√2[1/√2- sin0]
I = 2√2[1/√2]
I = 2
Therefore, the value of 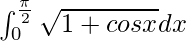 is 2.
is 2.
Question 26. 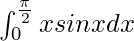
Solution:
We have,
I = 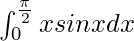
By using integration by parts, we get,
I = x ∫sinxdx – ∫(∫sin x (1)dx)dx
I = -xcosx – ∫(∫sin xdx)dx
I = -xcosx + ∫cosxdx
I = -xcosx + sinx
So we get,
I = ![Rendered by QuickLaTeX.com \left[-xcosx+sinx\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aa7ca59f4b7a5c234e6e8b185fc39f89_l3.png)
I = [-π/2cosπ/2 + sinπ/2 + 0 – 0]
I = 0 + 1 + 0 – 0
I = 1
Therefore, the value of 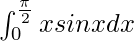 is 1.
is 1.
Question 27. 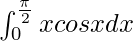
Solution:
We have,
I = 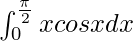
By using integration by parts, we get,
I = x∫cosxdx – ∫(∫cos x (1)dx)dx
I = xsinx – ∫(∫cosxdx)dx
I = xsinx – ∫sinxdx
I = x sin x + cos x
So we get,
I = ![Rendered by QuickLaTeX.com \left[xsinx+cosx\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4285f31ec916ff40ab7bda12024b1700_l3.png)
I = [π/2sinπ/2 + cosπ/2 – 0 – cos0]
I = π/2 + 0 – 0 – 1
I = π/2 – 1
Therefore, the value of 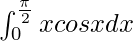 is π/2 – 1.
is π/2 – 1.
Question 28. 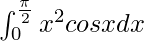
Solution:
We have,
I = 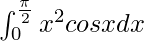
By using integration by parts, we get,
I = x2sinx – ∫(2x∫(cosx)dx)dx
I = x2sinx – ∫(2xsinx)dx
I = x2sinx – 2[-xcosx – ∫(1∫sinxdx)dx]
I = x2sinx – 2[-xcosx + ∫sinxdx]
I = x2sinx – 2[-xcosx + sinx]
I = x2sinx + 2xcosx – 2sinx
So we get,
I = ![Rendered by QuickLaTeX.com \left[x^2sinx+2xcosx-2sinx\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a3b09c6a0a320d195c1e3ef7b6795e18_l3.png)
I = [(π/2)2sinπ/2 + 2(π/2)cosπ/2 – 2sinπ/2 – 0 – 0 + sin0]
I = [π2/4 + 0 – 2 – 0 – 0 + 0]
I = π2/4 – 2
Therefore, the value of 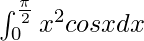 is π2/4 – 2.
is π2/4 – 2.
Question 29. 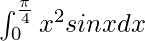
Solution:
We have,
I = 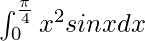
By using integration by parts, we get,
I = -x2cosx – ∫(2x∫sinxdx)dx
I = -x2cosx + ∫(2xcosx)dx
I = -x2cosx + 2[xsinx – ∫(∫cosxdx)dx]
I = -x2cosx + 2[xsinx – ∫sinxdx]
I = -x2cosx + 2[xsinx + cosx]
I = -x2cosx + 2xsinx + 2cosx
So we get,
I = ![Rendered by QuickLaTeX.com \left[-x^2cosx+2xsinx+2cosx\right]^{\frac{\pi}{4}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ae64dab610a09a919f50a26948e6d209_l3.png)
I = -(π/4)2cosπ/4 + 2π/4sinπ/4 + 2cosπ/4 + 0 – 0 – 2
I = –π2/16(1/ √2) + π/2(1/√2) + 2(1/√2) + 0 – 0 – 2
I = –π2/16√2 + π/2√2 + √2 – 2
Therefore, the value of 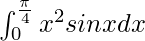 is -π2/16√2 + π/2√2 + √2 – 2.
is -π2/16√2 + π/2√2 + √2 – 2.
Question 30. 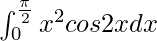
Solution:
We have,
I = 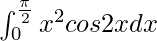
By using integration by parts, we get,
I = 1/2x2sin2x – ∫(2x∫cos2xdx)dx
I = 1/2x2sin2x – ∫(xsin2x)dx
I = 1/2x2sin2x – [-1/2xcos2x – ∫(∫sin2xdx)dx]
I = 1/2x2sin2x – [-1/2xcos2x + ∫1/2 cos2xdx]
I = 1/2x2sin2x – [-1/2xcos2x + 1/4sin2xdx]
I = 1/2x2sin2x + 1/2xcos2x – 1/4sin2xdx
So we get,
I = ![Rendered by QuickLaTeX.com \left[\frac{1}{2}x^2sin2x+\frac{1}{2}xcos2x-\frac{1}{4}sin2xdx\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-414f45cbdccb043ef79a408e4efd14c1_l3.png)
I = [1/2(π2/4)sinπ + 1/2(π/2)cosπ – 0 – 0 – 0 + 0]
I = -π/4
Therefore, the value of 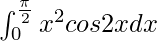 is -π/4.
is -π/4.
Question 31. 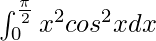
Solution:
We have,
I = 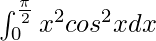
I = 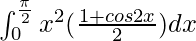
I = 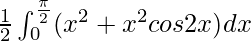
I = 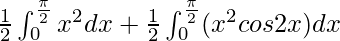
By using integration by parts, we get,
I = 1/2[x3/3] + x2sin2x/2 – [x ∫sin2x – ∫(∫sin2xdx)dx]
I = 1/2[x3/3] + x2sin2x/2 + xcosx/2 – sin2x/4
So we get,
I = ![Rendered by QuickLaTeX.com \left[\frac{1}{2}[\frac{x^3}{3}]+\frac{x^2sin2x}{2}+\frac{xcosx}{2}-\frac{sin2x}{4}\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b3bbb3879a9d263c0ab554cf48cd640a_l3.png)
I = [1/6[π3/8] + 0 + 0 – π/8]
I = π3/48 – π/8
Therefore, the value of 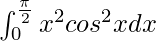 is π3/48 – π/8.
is π3/48 – π/8.
Question 32. 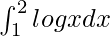
Solution:
We have,
I = 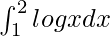
By using integration by parts, we get,
I = 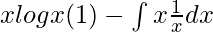
I = xlogx – ∫1dx
I = xlogx – x
So we get,
I = ![Rendered by QuickLaTeX.com \left[xlogx-x\right]^2_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7addb46cca1376caf285bb67c0b4c4cf_l3.png)
I = 2log2 – 2 – log1 + 1
I = 2 log 2 – 1
Therefore, the value of 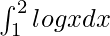 is 2 log 2 – 1.
is 2 log 2 – 1.
Question 33. 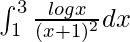
Solution:
We have,
I = 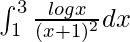
By using integration by parts, we get,
I = 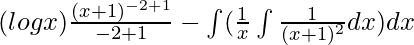
I = 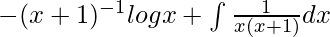
I = 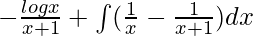
I = 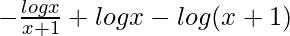
So we get,
I = ![Rendered by QuickLaTeX.com \left[-\frac{logx}{x+1}+logx - log(x+1)\right]^3_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-92eb41692f3ce1a9f4a1fac71725c4b4_l3.png)
I = -log3/4 + log3 – log4 + log1/2 – log1 + log2
I = log3(1 – 1/4) – 2log2 + 0 – 0 + log2
I = 3/4log3 – log2
Therefore, the value of 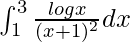 is 3/4log3 – log2.
is 3/4log3 – log2.
Question 34. 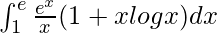
Solution:
We have,
I = 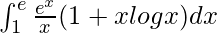
I = 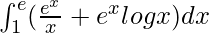
I = 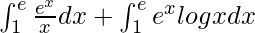
By using integration by parts, we get,
I = 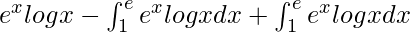
I = exlogx
So we get,
I = ![Rendered by QuickLaTeX.com \left[e^xlogx\right]^e_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cbcd01eb96f2530b6e446372e9d03060_l3.png)
I = eeloge – e1log1
I = ee (1) – 0
I = ee
Therefore, the value of 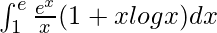 is ee.
is ee.
Question 35. 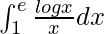
Solution:
We have,
I = 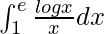
Let log x = t, so we have,
=> (1/x) dx = dt
Now, the lower limit is, x = 1
=> t = log x
=> t = log 1
=> t = 0
Also, the upper limit is, x = e
=> t = log x
=> t = log e
=> t = 1
So, the equation becomes,
I = 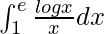
I = 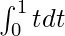
I = ![Rendered by QuickLaTeX.com \left[\frac{t^2}{2}\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c5e346021330c4a8ef2df592857430d_l3.png)
I = 1/2 – 0/2
I = 1/2
Therefore, the value of 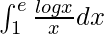 is 1/2.
is 1/2.
Question 36. 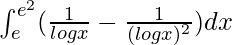
Solution:
We have,
I = 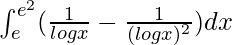
I = 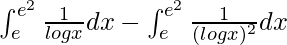
By using integration by parts, we get,
I = ![Rendered by QuickLaTeX.com \frac{x}{logx}-\int [(\frac{-1}{(logx)^2})(\frac{1}{x})\int dx]dx -\int \frac{1}{(logx)^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-560a1cfd7df1c339f2b6348418a7205d_l3.png)
I = 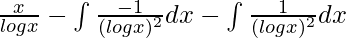
I = 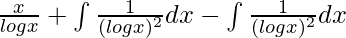
I = x/logx
So we get,
I = ![Rendered by QuickLaTeX.com \left[\frac{x}{logx}\right]^{e^2}_e](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c41bee9ad48fab71e4ef0cd7571b6d82_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{e^2}{loge^2}-\frac{e}{loge}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ce2e6e128e5ba9caf32ca79137620182_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{e^2}{2loge}-e\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e96aa1d7a6638f9ea2cfd7a24b8cfe49_l3.png)
I = e2/2 – e
Therefore, the value of 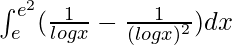 is e2/2 – e.
is e2/2 – e.
Question 37. 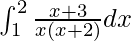
Solution:
We have,
I = 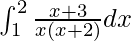
I = 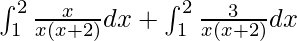
I = 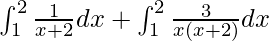
I = 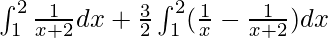
I = ![Rendered by QuickLaTeX.com \left[log(x+2)\right]^2_1+\left[\frac{3}{2}logx-\frac{3}{2}log(x+2)\right]^2_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18ea79082e40c92777b8f104bd7730ef_l3.png)
I = ![Rendered by QuickLaTeX.com \left[log(x+2)\right]^2_1+\left[\frac{3}{2}logx-\frac{3}{2}log(x+2)\right]^2_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18ea79082e40c92777b8f104bd7730ef_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{3}{2}logx-\frac{1}{2}log(x+2)\right]^2_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1b23b09a6176d748a1e9a3cf847ba711_l3.png)
I = 1/2[3log2 – log4 + log3]
I = 1/2[3log2 – 2log2 + log3]
I = 1/2[log 2 – log 3]
I = 1/2[log6]
I = log6/2
Therefore, the value of 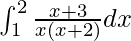 is log6/2.
is log6/2.
Question 38. 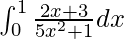
Solution:
We have,
I = 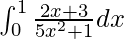
I = 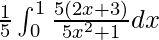
I = 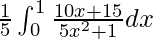
I = 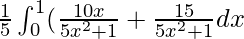
I = 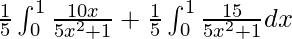
I = 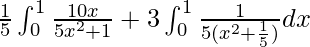
I = 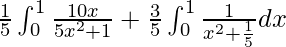
I = 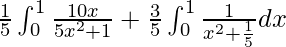
I = ![Rendered by QuickLaTeX.com \frac{1}{5}\left[log(5x^2+1)\right]^1_0+\left[\frac{3}{5}(\frac{1}{\frac{1}{\sqrt{5}}})tan^{-1}\frac{x}{\frac{1}{\sqrt{5}}}\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0f228b21737ca59dc90cee0b755569e6_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{5}\left[log(5x^2+1)\right]^1_0+\left[\frac{3}{\sqrt{5}}tan^{-1}\sqrt{5}x\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-35cc75fa111655ca12bf3afc44ef1b81_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{5}\left[log(5x^2+1)\right]^1_0+\left[\frac{3}{\sqrt{5}}tan^{-1}\sqrt{5}x\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-35cc75fa111655ca12bf3afc44ef1b81_l3.png)
I = [1/5log6 + 3/√5tan-1(√5) – 1/5log1 – 3/√5tan-1(0)]
I = [1/5 log6 + 3√5 tan-1(√5) – 0 – 0]
I = 1/5 log6 + 3√5 tan-1(√5)
Therefore, the value of 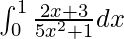 is 1/5 log6 + 3√5 tan-1(√5).
is 1/5 log6 + 3√5 tan-1(√5).
Question 39. 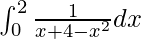
Solution:
We have,
I = 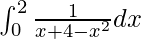
I = 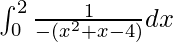
I = 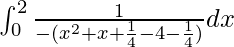
I = 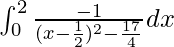
I = 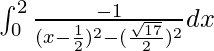
I = 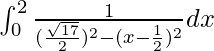
Let x – 1/2 = t, so we have,
=> dx = dt
Now, the lower limit is, x = 0
=> t = x – 1/2
=> t = 0 – 1/2
=> t = 1/2
Also, the upper limit is, x = 2
=> t = x – 1/2
=> t = 2 – 1/2
=> t = 3/2
So, the equation becomes,
I = 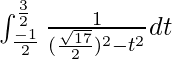
I = ![Rendered by QuickLaTeX.com \left[\frac{1}{2(\frac{\sqrt{17}}{2})}log\frac{\frac{\sqrt{17}}{2}+t}{\frac{\sqrt{17}}{2}-t}\right]^{\frac{3}{2}}_{\frac{-1}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-562ac3f9c240f5a66e18fc5243d23a61_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{\sqrt{17}}\left[log\frac{\frac{\sqrt{17}}{2}+\frac{3}{2}}{\frac{\sqrt{17}}{2}-\frac{3}{2}}-log\frac{\frac{\sqrt{17}}{2}-\frac{1}{2}}{\frac{\sqrt{17}}{2}+\frac{1}{2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-49669824fd492bd39218be251feda718_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{\sqrt{17}}\left[log\frac{\sqrt{17}+3}{\sqrt{17}-3}-log\frac{\sqrt{17}-1}{\sqrt{17}+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-57320a52156c35f4f388dde837923b76_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{\sqrt{17}}\left[log(\frac{\sqrt{17}+3}{\sqrt{17}-3}×\frac{\sqrt{17}+1}{\sqrt{17}-1})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-447d93be160769bf226d066349c16c3a_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{\sqrt{17}}\left[\log\frac{17+3+4\sqrt{17}}{17+3-4\sqrt{17}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d2f36e76ac8dc0c86440b7e2c8614316_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{\sqrt{17}}\left[\log\frac{20+4\sqrt{17}}{20-4\sqrt{17}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-736d0fa969317c1f581ef402b935c2c7_l3.png)
I = 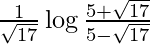
I = 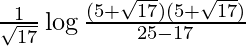
I = 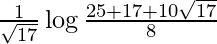
I = 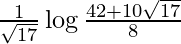
I = 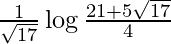
Therefore, the value of 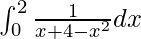 is
is 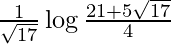 .
.
Question 40. 
Solution:
We have,
I = 
I = 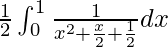
I = 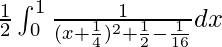
I = 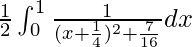
I = 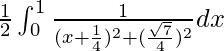
I = ![Rendered by QuickLaTeX.com \left[\frac{1}{2}\frac{4}{\sqrt{7}}\tan^{-1}(\frac{x+\frac{1}{4}}{\frac{\sqrt{7}}{4}})\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c9d7b11410a5a98467c5427e0b0586d6_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{4}{2\sqrt{7}}\tan^{-1}(\frac{x+\frac{1}{4}}{\frac{\sqrt{7}}{4}})\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-084917ed9640ef8d40167fb7f2f1206c_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{4}{2\sqrt{7}}\left[\tan^{-1}(\frac{\frac{5}{4}}{\frac{\sqrt{7}}{4}})-\tan^{-1}(\frac{\frac{1}{4}}{\frac{\sqrt{7}}{4}})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e303c8083796eca125cb325dd8af4170_l3.png)
I = 4/2√7[tan-1(5/√7) – tan-1(1/√7)]
I = 2/√7[tan-1(5/√7) – tan-1(1/√7)]
Therefore, the value of 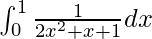 is 2/√7[tan-1(5/√7) – tan-1(1/√7)].
is 2/√7[tan-1(5/√7) – tan-1(1/√7)].
Question 41. 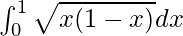
Solution:
We have,
I = 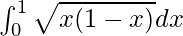
Let x = sin2 t, so we have,
=> dx = 2 sin t cos t dt
Now, the lower limit is, x = 0
=> sin2 t = 0
=> sin t = 0
=> t = 0
Also, the upper limit is, x = 1
=> sin2 t = 1
=> sin t = 1
=> t = π/2
So, the equation becomes,
I = 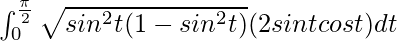
I = 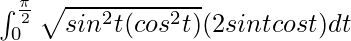
I = 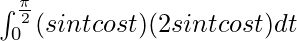
I = 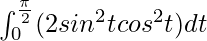
I = 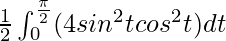
I = 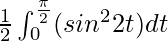
I = 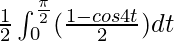
I = 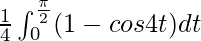
I = 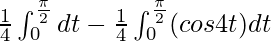
I = ![Rendered by QuickLaTeX.com \frac{1}{4}\left[t\right]^{\frac{\pi}{2}}_0-\frac{1}{4}\left[\frac{sin4t}{4}\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0e263766c7ad245c0ffd90107b894ab_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{4}\left[t\right]^{\frac{\pi}{2}}_0-\frac{1}{16}\left[sin4t\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1081f02ab85596bd7acb2874efa95bd7_l3.png)
I = 1/4[π/2 – 0] – 1/16[sin2π – 0]
I = 1/4[π/2] – 1/16[0 – 0 ]
I = π/8
Therefore, the value of 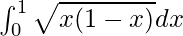 is π/8.
is π/8.
Question 42. 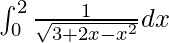
Solution:
We have,
I = 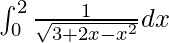
I = 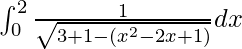
I = 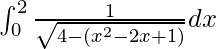
I = 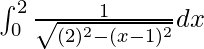
I = ![Rendered by QuickLaTeX.com \left[sin^{-1}(\frac{x-1}{2})\right]_{0}^{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5870af1122788a1ca3545e3443b03095_l3.png)
I = [sin-1(1/2) – sin-1(-1/2)]
I = π/6 -(-π/6)
I = π/6 + π/6
I = π/3
Therefore, the value of 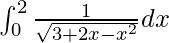 is π/3.
is π/3.
Question 43. 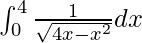
Solution:
We have,
I = 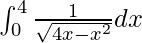
I = 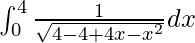
I = 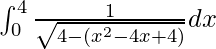
I = 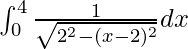
I = ![Rendered by QuickLaTeX.com \left[sin^{-1}(\frac{x-2}{2})\right]^4_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc088d39da2516679d751fb14c399661_l3.png)
I = ![Rendered by QuickLaTeX.com \left[sin^{-1}(\frac{4-2}{2})-sin^{-1}(\frac{0-2}{2})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d7f62f5aa991b2202ae205dccef62638_l3.png)
I = [sin-1(2/2) – sin-1(-2/2)]
I = sin-11 – sin-1(-1)
I = π/2 – (-π/2)
I = π/2 + π/2
I = π
Therefore, the value of 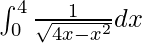 is π.
is π.
Question 44. 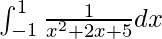
Solution:
We have,
I = 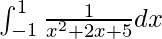
I = 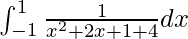
I = 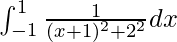
Let x + 1 = t, so we have,
=> dx = dt
Now, the lower limit is, x = –1
=> t = x + 1
=> t = – 1 + 1
=> t = 0
Also, the upper limit is, x = 1
=> t = x + 1
=> t = 1 + 1
=> t = 2
So, the equation becomes,
I = 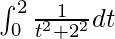
I = ![Rendered by QuickLaTeX.com \left[\frac{1}{2}tan^{-1}\frac{t}{2}\right]^2_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-072e8cec1ca44694f8f231f05a2db4c3_l3.png)
I = 1/2tan-12/2 – 1/2tan-10/2
I = 1/2tan-11 – 1/2tan-10
I = 1/2(π/4) – 0
I = π/8
Therefore, the value of 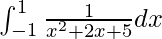 is π/8.
is π/8.
Share your thoughts in the comments
Please Login to comment...