Class 12 RD Sharma Solutions – Chapter 20 Definite Integrals – Exercise 20.1 | Set 3
Last Updated :
26 May, 2021
Evaluate the following definite integrals:
Question 45. 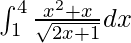
Solution:
We have,
I = 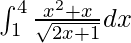
Let 2x + 1 = t2, so we have,
=> 2 dx = 2t dt
=> dx = t dt
Now, the lower limit is, x = 1
=> t2 = 2x + 1
=> t2 = 2(1) + 1
=> t2 = 3
=> t = √3
Also, the upper limit is, x = 4
=> t2 = 2x + 1
=> t2 = 2(4) + 1
=> t2 = 9
=> t = 3
So, the equation becomes,
I = 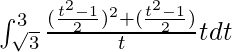
I = 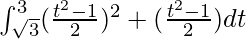
I = 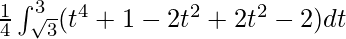
I = 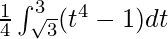
I = ![Rendered by QuickLaTeX.com \frac{1}{4}\left[\frac{t^5}{5}-t\right]^3_{\sqrt{3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d9cb3a47e2c5b649a6f190d1367bb5e6_l3.png)
I = 1/4 [35/5 – 3 – (√3)5/5 + √3]
I = 1/4[243/5 – 3 – 9√3/5 + √3]
I = 1/4((243 – 15 – 9√3 + 5√3)/5)
I = 1/4[(228 – 4√3)/5]
I = 1/4[4(57 – √3)/5]
I = (57 – √3)/5
Therefore, the value of 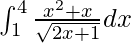 is (57 – √3)/5.
is (57 – √3)/5.
Question 46. 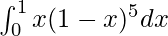
Solution:
We have,
I = 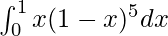
By using binomial theorem in the expansion of (1 – x)5, we get,
I = ![Rendered by QuickLaTeX.com \int_{0}^{1} x[1^5+^5C_1(-x)+^5C_2(-x)^2+^5C_3(-x)^3+^5C_4(-x)^4+^5C_5(-x)^5]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0f3594bc96b9057a313ad1ba6cb7130_l3.png)
I = 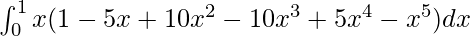
I = 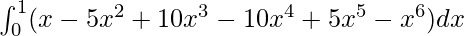
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2}{2}-\frac{5x^3}{3}+\frac{10x^4}{4}-\frac{10x^5}{5}+\frac{5x^6}{6}-\frac{x^7}{7}\right]^{1}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2a65957461dff0cc8e5491fa270e124c_l3.png)
I = 1/2 – 5/3 + 10/4 – 10/5 + 5/6 – 1/7
I = 1/2 – 5/3 + 5/3 – 2 + 5/6 – 1/7
I = 1/2 – 2 + 5/6 – 1/7
I = 1/42
Therefore, the value of 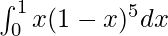 is 1/42.
is 1/42.
Question 47. 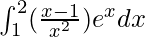
Solution:
We have,
I = 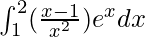
I = 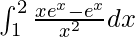
I = 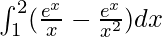
I = 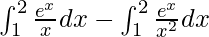
By using integration by parts, we get,
I = 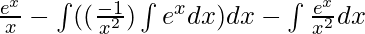
I = 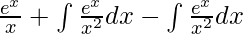
I = ex/x
So we get,
I = ![Rendered by QuickLaTeX.com \left[\frac{e^x}{x}\right]^2_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-61a0a8159e4f74ef18e9ee720300c8ef_l3.png)
I = e2/2 – e1/1
I = e2/2 – e
Therefore, the value of 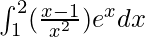 is e2/2 – e.
is e2/2 – e.
Question 48. 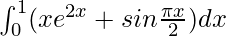
Solution:
We have,
I = 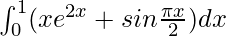
By using integration by parts in first integral, we get,
I = ![Rendered by QuickLaTeX.com \frac{xe^{2x}}{2}-\frac{1}{2}\int e^{2x}dx+\left[\frac{-cos\frac{\pi x}{2}}{\frac{\pi}{2}}\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-60be5e9eccc6354f203d327850e1fe49_l3.png)
I = xe2x/2 – (1/2)(e2x/2) + 2/π[1 – 0]
I = xe2x/2 – e2x/4 + 2/π
So we get,
I = ![Rendered by QuickLaTeX.com \left[\frac{xe^{2x}}{2}-\frac{e^{2x}}{4}\right]^1_0+\frac{2}{\pi}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a1a80263b9fbf069c4c5f2ad5ad6e579_l3.png)
I = [e2/2 + e2/4 – 0 + 1/4] + 2/π
I = e2/4 + 1/4 + 2/π
Therefore, the value of 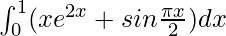 is e2/4 + 1/4 + 2/π.
is e2/4 + 1/4 + 2/π.
Question 49. 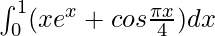
Solution:
We have,
I = 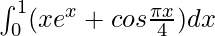
By using integration by parts in first integral, we get,
I = ![Rendered by QuickLaTeX.com xe^{x}-\int ((1)\int e^xdx)dx+ \left[\frac{sin\frac{\pi x}{4}}{\frac{\pi x}{4}}\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-87f6a51deccf55cb84aff39019bae06e_l3.png)
I = ![Rendered by QuickLaTeX.com xe^{x}-\int e^xdx+\frac{4}{\pi}[\frac{1}{\sqrt{2}}-0]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b6e01e553358fd42c4aba48d7ee4083c_l3.png)
I = ![Rendered by QuickLaTeX.com xe^{x}-e^x+\frac{4}{\pi}[\frac{1}{\sqrt{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-31e87550f1141ff1ef3f06779dead263_l3.png)
I = 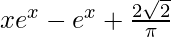
So we get,
I = ![Rendered by QuickLaTeX.com \left[xe^{x}-e^x\right]^1_0+\frac{2\sqrt{2}}{\pi}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f14dbbd187b638c527be7eeed4f8fe6c_l3.png)
I = ![Rendered by QuickLaTeX.com \left[e^{x}(x-1)\right]^1_0+\frac{2\sqrt{2}}{\pi}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b1a115baa619cd95abcf96faae3803da_l3.png)
I = [e1(1 – 1) – e0(0 – 1)] + 2√2/π
I = [0 – (-1)] + 2√2/π
I = 1 + 2√2/π
Therefore, the value of 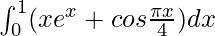 is 1 + 2√2/π.
is 1 + 2√2/π.
Question 50. 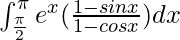
Solution:
We have,
I = 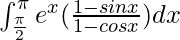
I = 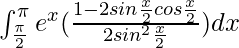
I = 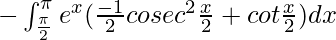
I = ![Rendered by QuickLaTeX.com \left[-e^xcot\frac{x}{2}\right]^\pi_\frac{\pi}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-66585943c187cd8454802893cbbe1945_l3.png)
I = -eπ cotπ/2 + eπ/2 cotπ/4
I = 0 + eπ/2(1)
I = eπ/2
Therefore, the value of 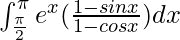 is eπ/2.
is eπ/2.
Question 51. 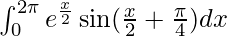
Solution:
We have,
I = 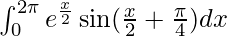
I = 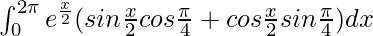
I = 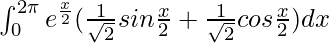
I = 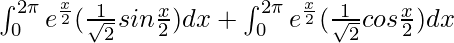
By using integration by parts in first integral, we get,
I = ![Rendered by QuickLaTeX.com \frac{1}{\sqrt{2}}\left[sin\frac{x}{2}\int_{0}^{2\pi} e^{\frac{x}{2}}dx-\int (\int (e^{\frac{x}{2}}dx)\frac{sin\frac{x}{2}}{2})dx\right]+\int_{0}^{2\pi} e^{\frac{x}{2}}(\frac{1}{\sqrt{2}}cos\frac{x}{2})dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-745255bc63e40c0ac010d1ce6690e258_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{\sqrt{2}}\left[sin\frac{x}{2}(2e^{\frac{x}{2}})\right]^{2\pi}_0-\int_{0}^{2\pi}e^{\frac{x}{2}}(\frac{1}{\sqrt{2}}cos\frac{x}{2})dx+\int_{0}^{2\pi}e^{\frac{x}{2}}(\frac{1}{\sqrt{2}}cos\frac{x}{2})dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54704aa9551f5825827b6c465b17de4d_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{\sqrt{2}}\left[sin\frac{x}{2}(2e^{\frac{x}{2}})\right]^{2\pi}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ef494528840171d067b512d3c07bb4ce_l3.png)
I = 1/√2[sinπ(2eπ) – 0]
I = 1/√2[0 – 0]
I = 0
Therefore, the value of 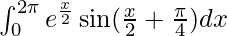 is 0.
is 0.
Question 52. 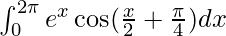
Solution:
We have,
I = 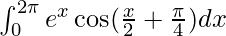
By using integration by parts, we get,
I = excos(x/2 + π/4) + 1/2∫exsin(x/2 + π/4)
I = ex cos(x/2 + π/4) + 1/2[ exsin(x/2 + π/4) – 1/2 ∫excos(x/2 + π/4)dx]
I = excos(x/2 + π/4) + 1/2exsin(x/2 + π/4) – 1/4I
![Rendered by QuickLaTeX.com \frac{5I}{4}=\left[e^x\cos(\frac{x}{2}+\frac{\pi}{4})+\frac{1}{2}e^xsin(\frac{x}{2}+\frac{\pi}{4})\right]^{2\pi}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-848d3385419a2872934406d8f58f1272_l3.png)
![Rendered by QuickLaTeX.com \frac{5I}{4}=\left[\frac{-1}{\sqrt{2}}(e^{2\pi}+1)-\frac{1}{2\sqrt{2}}(e^{2\pi}+1)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2216ab8058c4f6d059edcb1c5a058988_l3.png)
5I/4 = -3/ 2√2(e2π + 1)
I = -3√2/5(e2π + 1)
Therefore, the value of 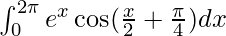 is -3√2/5(e2π + 1).
is -3√2/5(e2π + 1).
Question 53. 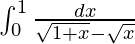
Solution:
We have,
I = 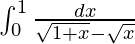
I = 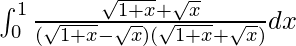
I = 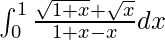
I = 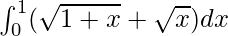
I = 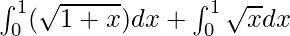
I = ![Rendered by QuickLaTeX.com \left[\frac{2}{3}(1+x)^{\frac{3}{2}}\right]^1_0+\left[\frac{2}{3}x^{\frac{3}{2}}\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-83103ec15687ef74fe0f42917c3c4078_l3.png)
I = 2/3[23/2 – 1] + 2/3[1 – 0]
I = 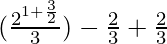
I = 25/2/3
Therefore, the value of 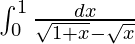 is 25/2/3.
is 25/2/3.
Question 54. 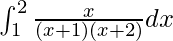
Solution:
We have,
I = 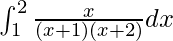
I = 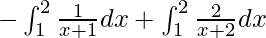
I = ![Rendered by QuickLaTeX.com -\left[log(x+1)\right]^2_1+\left[2log(x+2)\right]^2_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-354407da486f2b6e67ddcfacf54d43c3_l3.png)
I = ![Rendered by QuickLaTeX.com -\left[log(x+1)\right]^2_1+2\left[log(x+2)\right]^2_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8b48da63f9d999288850d721af7f4c74_l3.png)
I = -log3 + log2 + 2[log4 – log3]
I = -log3 + log2 + 2[2log2 – log3]
I = -log3 + log2 + 4log2 – 2log3
I = 5log2 – 3log3
I = log25 – log33
I = log32 – log27
I = log32/27
Therefore, the value of 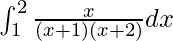 is log32/27.
is log32/27.
Question 55. 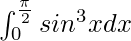
Solution:
We have,
I = 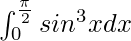
I = 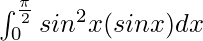
I = 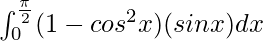
Let cos x = t, so we have,
=> – sin x dx = dt
Now, the lower limit is, x = 0
=> t = cos x
=> t = cos 0
=> t = 1
Also, the upper limit is, x = π/2
=> t = cos x
=> t = cos π/2
=> t = 0
So, the equation becomes,
I = 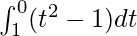
I = 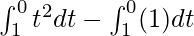
I = ![Rendered by QuickLaTeX.com \left[\frac{t^2}{3}\right]^{0}_1-\left[t\right]^0_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-579eee0a8f7b85f453a7492af49c03fb_l3.png)
I = [0 – 1/3] – [0 – 1]
I = [-1/3] – [-1]
I = -1/3 + 1
I = 2/3
Therefore, the value of 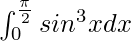 is 2/3.
is 2/3.
Question 56. 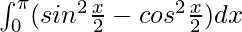
Solution:
We have,
I = 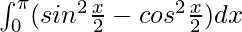
I = 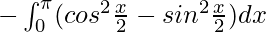
I = 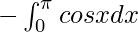
I = ![Rendered by QuickLaTeX.com \left[-sinx\right]^\pi_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4c90dd0e368e690804b1b76f90c76636_l3.png)
I = -sinπ + sin0
I = 0
Therefore, the value of 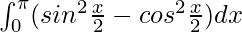 is 0.
is 0.
Question 57. 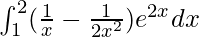
Solution:
We have,
I = 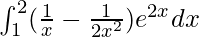
Let 2x = t, so we have,
=> 2x dx = dt
Now, the lower limit is, x = 1
=> t = 2x
=> t = 2(1)
=> t = 2
Also, the upper limit is, x = 2
=> t = 2x
=> t = 2(2)
=> t = 4
So, the equation becomes,
I = 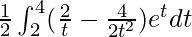
I = 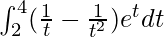
I = 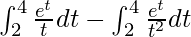
By using integration by parts in first integral, we get,
I = ![Rendered by QuickLaTeX.com \left[\frac{e^t}{t}\right]^4_2-\int (\frac{-1}{t^2}\int e^tdx)dx-\int_{2}^{4}\frac{e^t}{t^2}dt](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6f08417132a2cf12e467156744de78fa_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{e^t}{t}\right]^4_2+\int_{2}^{4}\frac{e^t}{t^2}dt-\int_{2}^{4}\frac{e^t}{t^2}dt](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d5ba0318179c56d53cccc6e0b15074a_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{e^t}{t}\right]^4_2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e769c55de831afc53cebadb99275d0f9_l3.png)
I = e4/4 – e2/2
Therefore, the value of 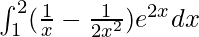 is e4/4 – e2/2.
is e4/4 – e2/2.
Question 58. 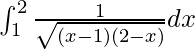
Solution:
We have,
I = 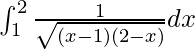
I = 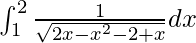
I = 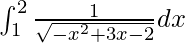
I = 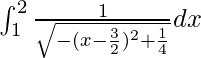
I = 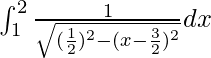
I = ![Rendered by QuickLaTeX.com \left[sin^{-1}(2x-3)\right]_{1}^{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e661acb88e503c4b1b84bb69eba82ab2_l3.png)
I = [sin-1(1) – sin-1(-1)]
I = π/2 – (-π/2)
I = π/2 + π/2
I = π
Therefore, the value of 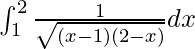 is π.
is π.
Question 59. If 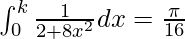 , find the value of k.
, find the value of k.
Solution:
We have,
=> 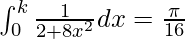
=> 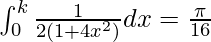
=> 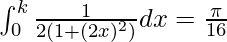
=> ![Rendered by QuickLaTeX.com \left[\frac{tan^{-1}2x}{4}\right]_{0}^{k}=\frac{\pi}{16}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d0c3c7052508955c69b33727098a051_l3.png)
=> tan-12k/4 – tan-10 = π/16
=> tan-12k/4 – 0 = π/16
=> tan-12k/4 = π/16
=> tan-12k = π/4
=> 2k = tanπ/4
=> 2k = 1
=> k = 1/2
Therefore, the value of k is 1/2.
Question 60. If 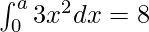 , find the value of k.
, find the value of k.
Solution:
We have,
=> 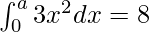
=> ![Rendered by QuickLaTeX.com \left[\frac{3(x^{2+1})}{2+1}\right]^a_0=8](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-814c1c1c6b7c8bbe6cb228912c886733_l3.png)
=> ![Rendered by QuickLaTeX.com \left[\frac{3(x^{3})}{3}\right]^a_0=8](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac82afd0d45be118d40a8ca9787aa6a5_l3.png)
=> ![Rendered by QuickLaTeX.com \left[x^3\right]^a_0=8](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cbc7a3d1ced8687b02067386eea72bc0_l3.png)
=> a3 – 0 = 8
=> a3 = 8
=> a = 2
Therefore, the value of a is 2.
Question 61. 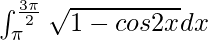
Solution:
We have,
I = 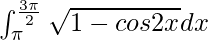
I = 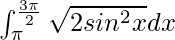
I = 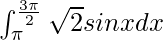
I = ![Rendered by QuickLaTeX.com -\left[\sqrt{2}cosx\right]_\pi^\frac{3\pi}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0f15823d34f530a6fb03be9d095192a7_l3.png)
I = -[√2cos3π/2 – √2cosπ]
I = -(-√2 – 0)
I = √2
Therefore, the value of 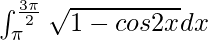 is √2.
is √2.
Question 62. 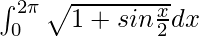
Solution:
We have,
I = 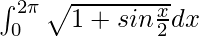
I = 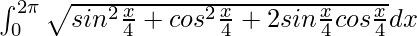
I = 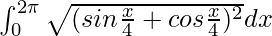
I = 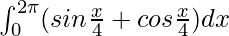
I = 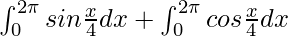
I = ![Rendered by QuickLaTeX.com \left[\frac{-cos\frac{x}{4}}{\frac{1}{4}}\right]_0^{2\pi}+\left[\frac{sin\frac{x}{4}}{\frac{1}{4}}\right]_0^{2\pi}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-01085648dd622aea79608e8621c68830_l3.png)
I = ![Rendered by QuickLaTeX.com \left[-4cos\frac{x}{4}\right]_0^{2\pi}+\left[4sin\frac{x}{4}\right]_0^{2\pi}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d395de192736877bb37105f0268d2256_l3.png)
I = [-4cosπ/2 + 4cos0] + [4sinπ/2 – 4sin0]
I = 0 + 4 + 4 – 0
I = 8
Therefore, the value of 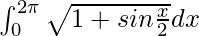 is 8.
is 8.
Question 63. 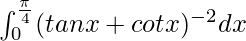
Solution:
We have,
I = 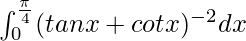
I = 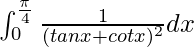
I = 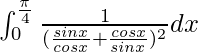
I = 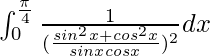
I = 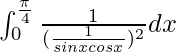
I = 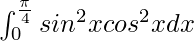
I = 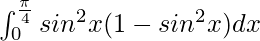
I = 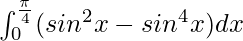
I = 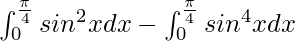
I = ![Rendered by QuickLaTeX.com \left[\frac{x}{2}-\frac{cosxsinx}{2}\right]^{\frac{\pi}{4}}_0-\left[\frac{3}{4}(\frac{x}{2}-\frac{cosxsinx}{2})-\frac{cosxsin^3x}{4}\right]^{\frac{\pi}{4}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d39033360b58790d23d8f70bee0ea8c0_l3.png)
I = 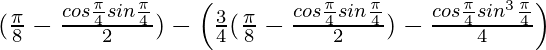
I = (π/8 – 1/4) – (3/4(π/8 – 1/4) – 1/16)
I = π/8 – 1/4 – (3π/32 – 3/16 – 1/16)
I = π/8 – 1/4 – (3π/32 – 1/4)
I = π/8 – 1/4 – 3π/32 + 1/4
I = π/8 – 3π/32
I = (4π – 3π)/32
I = π/32
Therefore, the value of 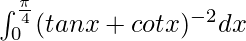 is π/32.
is π/32.
Question 64. 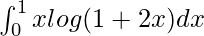
Solution:
We have,
I = 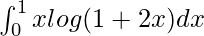
By using integration by parts we get,
I = 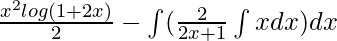
I = 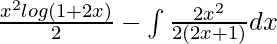
I = 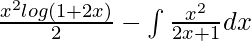
I = 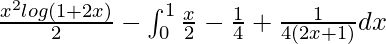
I = 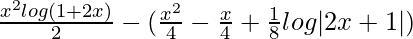
So we get,
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2log(1+2x)}{2}\right]^1_0-\left[\frac{x^2}{4}-\frac{x}{4}+\frac{1}{8}log|2x+1|)\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d1e6888483544046b74bae20684f8cd1_l3.png)
I = log3/2 – 1/8log3
I = 3/8log3
Therefore, the value of 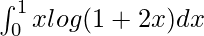 is 3/8log3.
is 3/8log3.
Question 65. 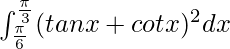
Solution:
We have,
I = 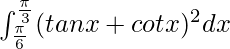
I = 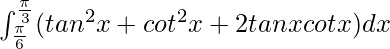
I = 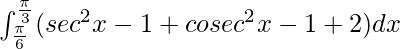
I = 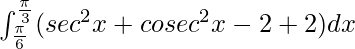
I = 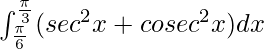
I = 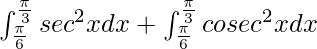
I = ![Rendered by QuickLaTeX.com \left[tanx\right]_{\frac{\pi}{6}}^{\frac{\pi}{3}}+\left[-cotx\right]_{\frac{\pi}{6}}^{\frac{\pi}{3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ed98f371d8f18a75c59fff936b2e01f3_l3.png)
I = [tanπ/3 – tanπ/6] + [-cotπ/3 + cotπ/6]
I = [√3 – 1/√3] + [- 1/√3 – √3]
I = 2[√3 – 1/√3]
I = 4/√3
Therefore, the value of 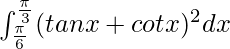 is 4/√3.
is 4/√3.
Question 66. 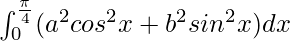
Solution:
We have,
I = 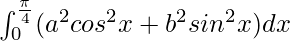
I = 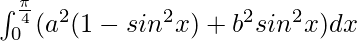
I = 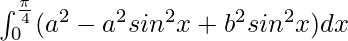
I = ![Rendered by QuickLaTeX.com \int_{0}^{\frac{\pi}{4}}[a^2-(b^2-a^2)sin^2x]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-872d2cc957290acba8f5f4def5303a68_l3.png)
I = ![Rendered by QuickLaTeX.com \int_{0}^{\frac{\pi}{4}}a^2dx-\int_{0}^{\frac{\pi}{4}}[(b^2-a^2)sin^2x]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1b6756e6e72734cb659550d0d4b53abd_l3.png)
I = 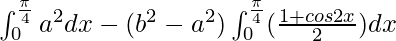
I = 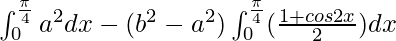
I = ![Rendered by QuickLaTeX.com \left[a^2x\right]_{0}^{\frac{\pi}{4}}+(b^2-a^2)[\frac{x}{2}+\frac{sin2x}{4}]_{0}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c467e42b31604c96c6e453b5c7dae3e9_l3.png)
I = 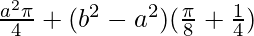
I = 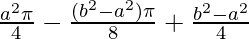
I = 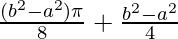
Therefore, the value of 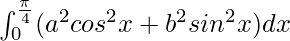 is
is 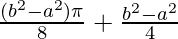 .
.
Question 67. 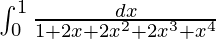
Solution:
We have,
I = 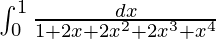
I = 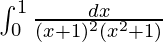
I = ![Rendered by QuickLaTeX.com \int_{0}^{1}[\frac{-x}{2(x^2+1)}+\frac{1}{2(x+1)}+\frac{1}{2(x+1)^2}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b8d056c9c6cd6ea0d46d85dac399f6d2_l3.png)
I = ![Rendered by QuickLaTeX.com -\left[\frac{log(x^2+1)}{4}\right]^1_0+\left[\frac{log(x+1)}{2}\right]^1_0-\left[\frac{1}{2(x+1)}\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1db2b27bf504b73590a8354dd52ce2f3_l3.png)
I = -log2/4 + log2/2 – 1/4 + 1/2
I = log2/4 + 1/4
Therefore, the value of 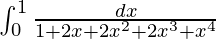 is log2/4 + 1/4.
is log2/4 + 1/4.
Share your thoughts in the comments
Please Login to comment...