Class 12 RD Sharma Solutions – Chapter 20 Definite Integrals – Exercise 20.3 | Set 2
Last Updated :
14 Jul, 2021
Evaluate the following integrals:
Question 15. 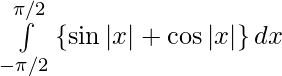
Solution:
We have,
I = 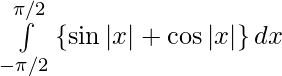
Since f(- x) = sin|- x| + cos|- x|
= sin |x| + cos |x|
= f(x)
So, f(x) is an even function.
Therefore, we get
I = 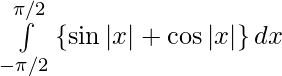
I = 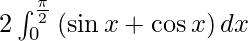
I = ![Rendered by QuickLaTeX.com 2 \left[ - \cos x + \sin x \right]_0^\frac{\pi}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b74fa44660c14d2878b14fc6f8380351_l3.png)
I = 2 (0 + 1 + 1 – 0)
I = 4
Question 16. 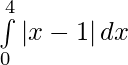
Solution:
We have,
I = 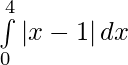
We know,
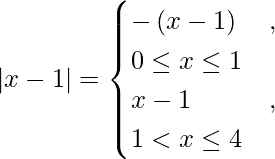
So we get,
I = 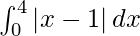
I = 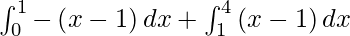
I = ![Rendered by QuickLaTeX.com \left[ - \frac{x^2}{2} + x \right]_0^1 + \left[ \frac{x^2}{2} - x \right]_1^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aa416dac73f45a0e162423a1c137c3c6_l3.png)
I = -1/2 + 1 – 0 + 8 – 4 – 1/2 + 1
I = 5
Question 17. 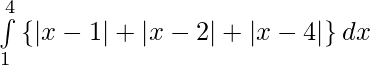
Solution:
We have,
I = 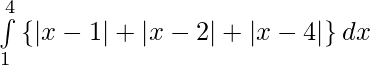
We know,
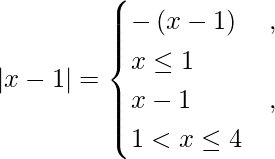
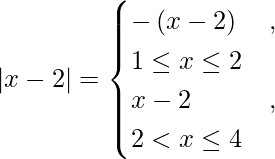
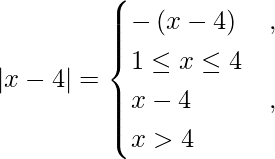
So we get,
I = 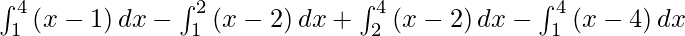
I = ![Rendered by QuickLaTeX.com \left[ \frac{x^2}{2} - x \right]_1^4 - \left[ \frac{x^2}{2} - 2x \right]_1^2 + \left[ \frac{x^2}{2} - 2x \right]_2^4 - \left[ \frac{x^2}{2} - 4x \right]_1^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-84fef62a3248152a8d1e2863aa3df05e_l3.png)
I = 8 – 4 – 1/2 + 1 – (2 – 4 – 1/2 + 2) + 8 – 8 – 2 + 4 – (8 – 16 – 1/2 + 4)
I = 23/2
Question 18. 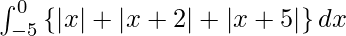
Solution:
We have,
I = 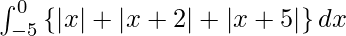
We know,
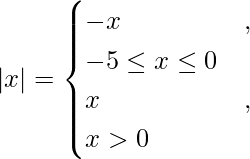
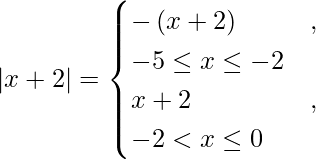
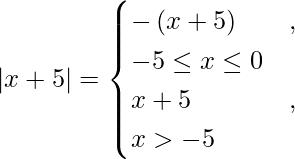
So we get,
I = 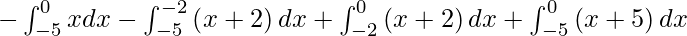
I = ![Rendered by QuickLaTeX.com - \left[ \frac{x^2}{2} \right]_{- 5}^0 - \left[ \frac{x^2}{2} + 2x \right]_{- 5}^{- 2} + \left[ \frac{x^2}{2} + 2x \right]_{- 2}^0 + \left[ \frac{x^2}{2} + 5x \right]_{- 5}^0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6532bd1a446b16d72f54a7090548f172_l3.png)
I = 25/2 – (2 – 4 – 25/2 + 10) – 2 + 4 + (-25/2 + 25)
I = 63/2
Question 19. 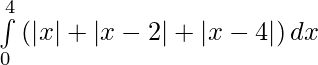
Solution:
We have,
I = 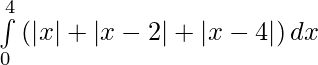
We know,
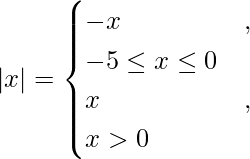
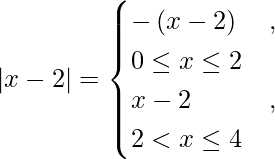
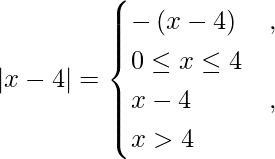
So we get,
I = 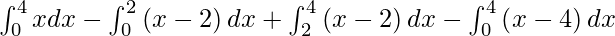
I = ![Rendered by QuickLaTeX.com \left[ \frac{x^2}{2} \right]_0^4 - \left[ \frac{x^2}{2} - 2x \right]_0^2 + \left[ \frac{x^2}{2} - 2x \right]_2^4 - \left[ \frac{x^2}{2} - 4x \right]_0^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-01012bb942aa70b5e05b3152ecd42ccc_l3.png)
I = 8 – (2 – 4) + 8 – 8 – 2 + 4 – (8 – 16)
I = 20
Question 20. 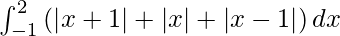
Solution:
We have,
I = 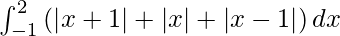
We know,
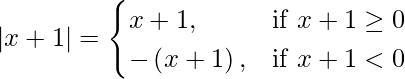
When –1 < x < 0,
|x + 1| + |x| + |x – 1| = x + 1 + (- x) + [-(x – 1)]
= 2 – x
And when 0 < x < 1,
|x + 1| + |x| + |x – 1| = x + 1 + x + [-(x – 1)]
= x + 2
And when 1 ≤ x ≤ 2,
|x + 1| + |x| + |x – 1| = x + 1 + x + x – 1
= 3x
So we get,
I = 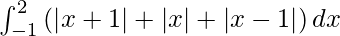
I = 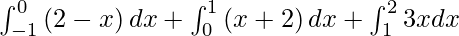
I = 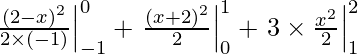
I = – 1/2(4 – 9) + 1/2( 9 – 4) + 3/2(4 – 1)
I = 5/2 + 5/2 + 9/2
I = 19/2
Question 21. 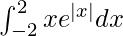
Solution:
We have,
I = 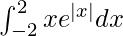
Now here,
f(- x) = (- x)e|- x|
= – x e|x|
= – f(x)
So, f(x) is an odd function.
Therefore we get,
I = 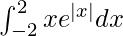
I = 0
Question 22. 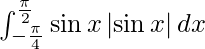
Solution:
We have,
I = 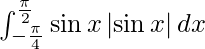
I = 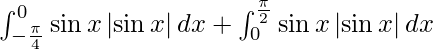
As we know, 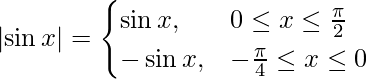
I = 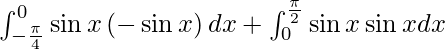
I = 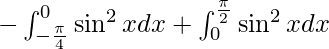
I = 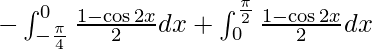
I = 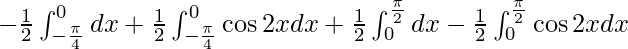
I = 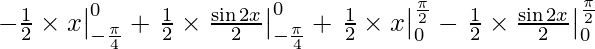
I = -1/2(0 + π/4) + 1/4(0 + sin π/2) + 1/2 ( π/2 – 0) – 1/4(sin π – 0)
I = – π/8 + 1/4 (0 + 1) + π/8 – 1/4 (0 – 0)
I = π/8 + 1/4
Question 23. 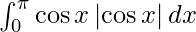
Solution:
We have,
I = 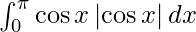
Now here,
f(π – x) = cos(π – x)|cos(π – x)|
= -cos x|-cos x|
= – cos x|cos x|
= – f(x)
So, f(x) is an odd function.
Therefore we get,
I = 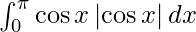
I = 0
Question 24. 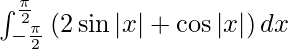
Solution:
We have,
I = 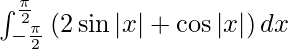
Now here,
f(- x) = 2sin|- x| + cos|- x|
= 2sin|x| + cos|x|
= f(x)
So, f(x) is an odd function.
Therefore we get,
I = 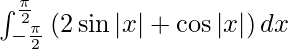
I = 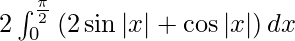
As we know, 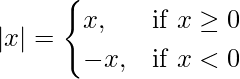
I = 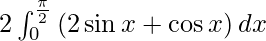
I = 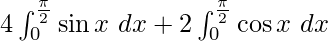
I = 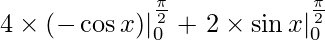
I = – 4(cos π/2 – cos 0) + 2(sin π/2 – sin 0)
I = –4 ( 0 – 1) + 2 (1 – 0)
I = 4 + 2
I = 6
Question 25. 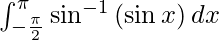
Solution:
We have,
I = 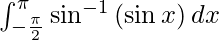
I = 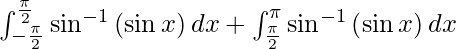
I = 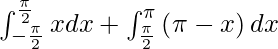
As π/2 ≤ x ≤ π, we get
=> –π ≤ –x ≤ –π/2
=> 0 ≤ π – x ≤ π/2
So, we get
I = 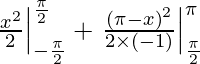
I = 1/2 (π2/4 – π2/4) – 1/2( 0 – π2/4)
I = 0 + π2/8
I = π2/8
Question 26. 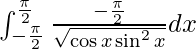
Solution:
We have,
I = 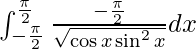
I = 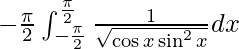
I = 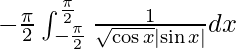
As we know, 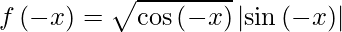
= √cos x|-sin x|
= √cos x|sin x|
= f(x)
So, f(x) is an odd function.
Therefore we get,
I = 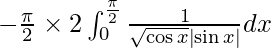
I = 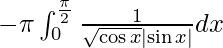
As we know, 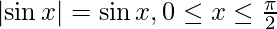 ,
,
I = 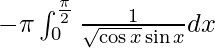
I = 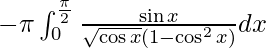
Let cos x = z2. So, we have
=> – sin x dx = 2z dz
Now, the lower limit is, x = 0
=> z2 = cos x
=> z2 = cos 0
=> z2 = 1
=> z = 1
Also, the upper limit is, x = π/2
=> z2 = cos x
=> z2 = cos π/2
=> z2 = 0
=> z = 0
So, the equation becomes,
I = 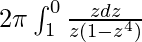
I = 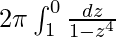
I = 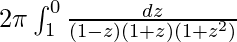
I = 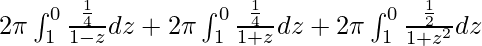
I = 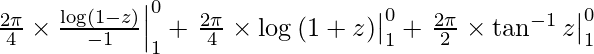
I = – π/2(log1 – log0) + π/2(log1 – log2) + π(tan-1 0 – tan-1 1)
I = – π/2[0 – ∞] + π/2(0 – log2) + π(0 – π/4)
I = -∞ – π/2 log2 – π2/4
I = –∞
Question 27. ![Rendered by QuickLaTeX.com \int_0^2 2x\left[ x \right]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8bf48ba5168164ed15afab5c016e7656_l3.png)
Solution:
We have,
I = ![Rendered by QuickLaTeX.com \int_0^2 2x\left[ x \right]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8bf48ba5168164ed15afab5c016e7656_l3.png)
I = ![Rendered by QuickLaTeX.com \int_0^1 2x\left[ x \right]dx + \int_1^2 2x\left[ x \right]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-98a6cdc161db6ff52f4b0d382c9a528b_l3.png)
As we know, ![Rendered by QuickLaTeX.com \left[ x \right] = \begin{cases}0, & 0 \leq x < 1 \\ 1, & 1 \leq x < 2\end{cases}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-714e1693fe24017dd758e61a577d52c1_l3.png)
I = 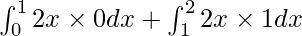
I = 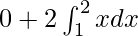
I = 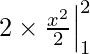
I = 4 – 1
I = 3
Question 28. 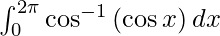
Solution:
We have,
I = 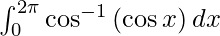
I = 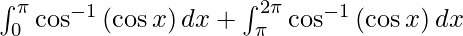
As we know, π ≤ x ≤ 2π
=> –2π ≤ –x ≤ –π
=> 0 ≤ 2π – x ≤ π
Therefore, we get
I = 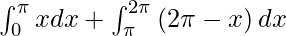
I = 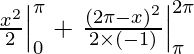
I = 1/2( π – 0) – 1/2(0 – π)
I = π2/2 + π2/2
I = π2
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...