Class 12 RD Sharma Solutions – Chapter 11 Differentiation – Exercise 11.7 | Set 2
Last Updated :
20 May, 2021
Question 11. Find , when
, when 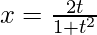 and
and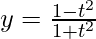
Solution:
Here,
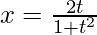
Differentiating it with respect to t using quotient rule,
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\left[\frac{(1+t^2)\frac{d}{dt}(2t)-2t\frac{d}{dt}(1+t^2)}{(1+t^2)^2}\right]\\ =\left[\frac{(1+t^2)(2)-2t(2t)}{(1+t^2)^2}\right]\\ =\left[\frac{2+2t^2-4t^2}{(1+t^2)^2}\right]\\ =\left[\frac{2+2t^2-4t^2}{(1+t^2)^2}\right]\\ =\left[\frac{2-2t^2}{(1+t^2)^2}\right]\\ \frac{dx}{dt}=\frac{2(1-t^2)}{(1+t^2)^2}\ \ \ \ \ ....(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9ee06fc588779f3b900b93e0c709fad0_l3.png)
and,
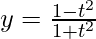
Differentiating it with respect to t using quotient rule,
![Rendered by QuickLaTeX.com \frac{dy}{dt}=\left[\frac{(1+t^2)\frac{d}{dt}(1-t^2)-(1-t^2)\frac{d}{dt}(1+t^2)}{(1+t^2)^2}\right]\\ =\left[\frac{(1+t^2)(-2t)-(1-t^2)(2t)}{(1+t^2)^2}\right]\\ =\left[\frac{-2t-2t^3-2t+2t^3}{(1+t^2)^2}\right]\\ \frac{dy}{dt}=\frac{-4t}{(1+t^2)^2}\ \ \ \ \ ....(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1a740e3b5a78505a2ee9fa66e8c6d112_l3.png)
Dividing equation (2) by (1)
![Rendered by QuickLaTeX.com \frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{-4t}{(1+t^2)^2}\times\frac{(1+t^2)^2}{2(1-t^2)}\\ =\frac{-2t}{1-t^2}\\ \frac{dy}{dx}=-\frac{x}{y}\ \ \ \ \left[Since,\ \frac{x}{y}=\frac{2t}{1+t^2}\times\frac{1+t^2}{1-t^2}=\frac{2t}{1-t^2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c22aa843c0a25f551c98e544a2c775ff_l3.png)
Question 12. Find , when
, when 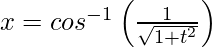 and
and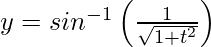
Solution:
Here,
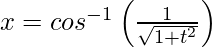
Differentiating it with respect to t using chain rule,
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\frac{-1}{\sqrt{1-\left(\frac{1}{1+t^2}\right)}^2}\frac{d}{dt}\left(\frac{1}{\sqrt{1+t^2}}\right)\\ =\frac{-1}{\sqrt{1-\frac{1}{(1+t^2)}}}\left[\frac{-1}{2(1+t^2)^{\frac{3}{2}}}\right]\frac{d}{dt}(1+t^2)\\ =\frac{(1+t^2)^{\frac{1}{2}}}{\sqrt{1+t^2-1}}\times\frac{-1}{2(1+t^2)^{\frac{3}{2}}}(2t)\\ =\frac{-t}{\sqrt{t^2}\times(1+t^2)}\\ \frac{dx}{dt}=\frac{-1}{1+t^2}\ \ \ \ \ ....(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-544c05e996df5d0f3296d5ffcfe10f02_l3.png)
Now,
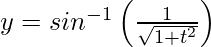
Differentiating it with respect to t using chain rule,
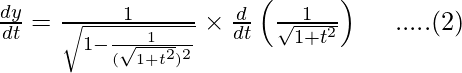
Dividing equation (2) by (1)
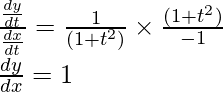
Question 13. Find , when
, when 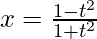 and
and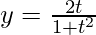
Solution:
Here,
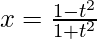
Differentiating it with respect to t using quotient rule,
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\left[\frac{(1+t^2)\frac{d}{dt}(1-t^2)-(1-t^2)\frac{d}{dt}(1+t^2)}{(1+t^2)^2}\right]\\ =\left[\frac{(1+t^2)(-2t)-(1-t^2)(2t)}{(1+t^2)^2}\right]\\ =\left[\frac{-2t-2t^3-2t+2t^3}{(1+t^2)^2}\right]\\ \frac{dx}{dt}=\frac{-4t}{(1+t^2)^2}\ \ \ \ \ ....(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3fb481a5b16b2d7627f1e238eca02ec3_l3.png)
and,
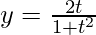
Differentiating it with respect to t using quotient rule,
![Rendered by QuickLaTeX.com \frac{dy}{dt}=\left[\frac{(1+t^2)\frac{d}{dt}(2t)-2t\frac{d}{dt}(1+t^2)}{(1+t^2)^2}\right]\\ =\left[\frac{(1+t^2)(2)-2t(2t)}{(1+t^2)^2}\right]\\ =\left[\frac{2+2t^2-4t^2}{(1+t^2)^2}\right]\\ \frac{dx}{dt}=\frac{2(1-t^2)}{(1+t^2)^2}\ \ \ \ \ ....(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e425a78e7a247622494ffc0567870996_l3.png)
Question 14. If x = 2cosθ – cos2θ and y = 2sinθ – sin2θ, prove that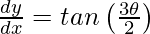
Solution:
Here,
x = 2cosθ – cos2θ
Differentiating it with respect to θ using chain rule,
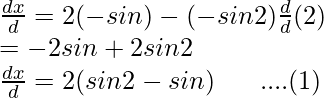
and,
y = 2sinθ – sin2θ
Differentiating it with respect to θ using chain rule,
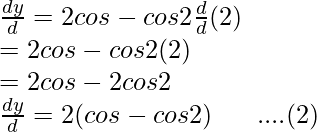
Dividing equation (2) by equation (1),
![Rendered by QuickLaTeX.com \frac{\frac{dy}{dθ}}{\frac{dx}{dθ}}=\frac{2(cosθ -cos2θ )}{2(sin2θ - sinθ )}\\ =\frac{cosθ -cos2θ}{sin2θ -sinθ}\\ \frac{dy}{dx}=\frac{-2sin\left(\frac{θ +2θ}{2}\right)sin\left(\frac{θ -2θ}{2}\right)}{2cos\left(\frac{2θ +θ}{2}\right)sin\left(\frac{2θ -θ}{2}\right)}\ \ \ \ \left[Since,\ sinA-sinB=2cos\left(\frac{A+B}{2}\right)sin\left(\frac{A-B}{2}\right),\ \ cosA-cosB=-2sin\left(\frac{A+B}{2}\right)sin\left(\frac{A-B}{2}\right)\right]\\ =\frac{-sin\left(\frac{3θ )}{2}\right)\left(sin\left(\frac{-θ}{2}\right)\right)}{cos\left(\frac{3θ}{2}\right)sin\left(\frac{θ}{2}\right)}\\ =\frac{sin\left(\frac{3θ}{2}\right)}{cos\left(\frac{3θ}{2}\right)}\\ \frac{dy}{dx}=tan\left(\frac{3θ}{2}\right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0bf01ba8efaf2f0053f5db5691afd620_l3.png)
Question 15. If x = ecos2t and y = esin2t prove that,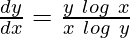
Solution:
Here,
x = ecos2t
Differentiating it with respect to t using chain rule,
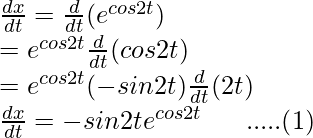
and,
y = esin2t
Differentiating it with respect to t using chain rule,
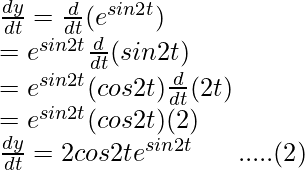
Dividing equation (2) by (1)
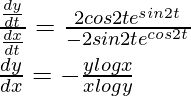
![Rendered by QuickLaTeX.com \left[Since,\ x=e^{cos2t}\Rightarrow logx=cos2t\ \ y=e^{sin2t}\Rightarrow logy=sin2t\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-345c478377223b0030ec043d61311bc7_l3.png)
Question 16. If x = cos t and y = sin t, prove that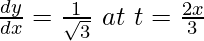
Solution:
Here,
x = cos t
Differentiating it with respect to t,
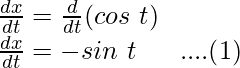
and,
y = sin t
Differentiating it with respect to t,
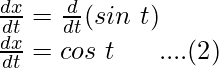
Dividing equation (2) by (1),
![Rendered by QuickLaTeX.com \frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{cos\ t}{-sin\ t}\\ \frac{dy}{dx}=-cot\ t\\ \left(\frac{dy}{dx}\right)=-cot\left(\frac{2\pi}{3}\right)\\ =-cot\left(\pi-\frac{\pi}{3}\right)\\ =-\left[-cot\left(\frac{\pi}{3}\right)\right]\\ =cot\left(\frac{\pi}{3}\right)\\ \frac{dy}{dx}=\frac{1}{\sqrt3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0b6b67bd521a85525ff50276b7e3aba0_l3.png)
Question 17. If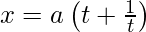 and
and 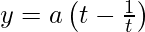 , Prove that
, Prove that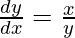
Solution:
Here,
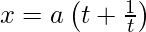
Differentiating it with respect to t,
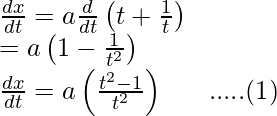
and,
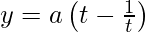
Differentiating it with respect to t,
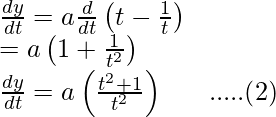
Dividing equation (2) by (1)
![Rendered by QuickLaTeX.com \frac{\frac{dy}{dt}}{\frac{dx}{dt}}=a\frac{(t^2+1)}{t^2}\times\frac{t^2}{a(t^2-1)}\\ \frac{dy}{dx}=\frac{t^2+1}{t^2-1}\\ \frac{dy}{dx}=\frac{x}{y}\ \ \ \ \ \ \left[Since,\ \frac{x}{y}=\frac{a(t^2+1)}{t}\times\frac{t}{a(t^2-1)}=\left(\frac{t^2+1}{t^2-1}\right)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-89bf3b0508009ed8959a0c2ab1cc5eb9_l3.png)
Question 18. If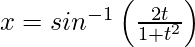 and
and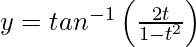 , -1 < 1 < 1, prove that
, -1 < 1 < 1, prove that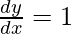
Solution:
Here,
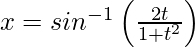
Put t = tan θ
![Rendered by QuickLaTeX.com x=sin^{-1}\left(\frac{2tanθ}{1+tan^2θ}\right)\\ =sin^{-1}(sin2θ )\\ =2θ \ \ \ \ \ \left[Since,\ sin\ 2x=\frac{2tan\ x}{1+tan^2x}\right]\\ x=2(tan^{-1}t)\ \ \ \ \ [Since,\ t=sin\ θ ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-860c73dd57a0c9e3e7dc3221b4435986_l3.png)
Differentiating it with respect to t,
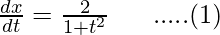
Further,
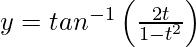
Put t = tan θ
![Rendered by QuickLaTeX.com y=tan^{-1}\left(\frac{2tanθ}{1+tan^2θ}\right)\\ =tan^{-1}(tan2θ )\\ =2θ \ \ \ \ \ \left[Since,\ tan\ 2x=\frac{2tan\ x}{1-tan^2x}\right]\\ y=2tan^{-1}t\ \ \ \ \ [Since,\ t=tan\ θ ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-db0638806ddda700e6b02f50355fa339_l3.png)
Differentiating it with respect to t,
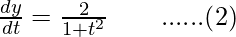
Dividing equation (2) by (1),
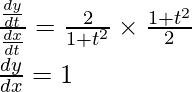
Question 19. If x and y are connected parametrically by the equation, without eliminating the parameter, find , when:
, when: 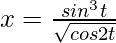 ,
,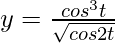
Solution:
Here, the given equations are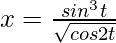 and
and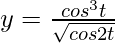
Thus,
![Rendered by QuickLaTeX.com \frac{dx}{dt}\frac{d}{dt}\left[\frac{sin^3t}{\sqrt{cos2t}}\right]\\ =\frac{\sqrt{cos2t}.\frac{d}{dt}(sin^3t)-sin^3t.\frac{d}{dt}\sqrt{cos2t}}{cos2t}\\ =\frac{\sqrt{cos2t}.3sin^2t.\frac{d}{dt}(sin\ t)-sin^3t\times\frac{1}{2\sqrt{cos\ 2t}}.\frac{d}{dt}(cos2t)}{cos2t}\\ =\frac{3\sqrt{cos\ 2t}.sin^2t\ cos\ t-\frac{sin^3t}{2\sqrt{cos\ 2t}}.(-2sin\ 2t)}{cos\ 2t}\\ =\frac{3cos\ 2t\ sin^2tcos\ t+sin^3tsin\ 2t}{cos\ 2t\sqrt{cos\ 2t}}\\ \frac{dy}{dt}=\frac{d}{dt}\left[\frac{cos^3t}{\sqrt{cos\ 2t}}\right]\\ =\frac{\sqrt{cos\ 2t}.\frac{d}{dt}(cos^3t)-cos^3t.\frac{d}{dt}(\sqrt{cos\ 2t})}{cos\ 2t}\\ =\frac{-3cos\ 2t.cos^2t.sin\ t+cos^3t\ sin\ 2t}{cos\ 2t.\sqrt{cos\ 2t}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7cd03429a47f591ae44c24aded7b129e_l3.png)
Therefore,
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{-3cos\ 2t.cos^2t. sin\ t+cos^3t\ sin\ 2t}{3cos\ 2t\ sin^2t\ cos\ t+sin^3t\ sin\ 2t}\\ =\frac{-3cos\ 2t\ cos^2t.sin\ t+cos^3t(2sin\ t\ cos\ t)}{3cos\ 2t\ sin^2t\ cos\ t+sin^3t(2sin\ t+2sin^3t)}\\ =\frac{[-3(2cos^2t-1)cos\ t+2cos^3t]}{[3(1-2sin^2t)sin\ t+2sin^3t]}\ \ \ \ \ \ \ [cos\ 2t=(2cos^2t-1),\ cos\ 2t=(1-2sin^2t)]\\ =\frac{-4cos^3t+3cos\ t}{3sin\ t-4sin^3\ t}\\ =\frac{-cos\ 3t}{sin\ 3t}\ \ \ \ \ \ [cos\ 3t=4cos^3t3cos\ t,\ sin\ 3t=3sin\ t-4sin^3t]\\ =-cot3t](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-61c1861c7248163175950fbf51cceae2_l3.png)
Question 20. If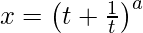 and
and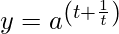 , find
, find
Solution:
Here,
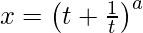
Differentiating it with respect to t using chain rule,
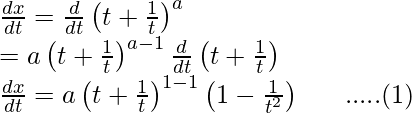
And,
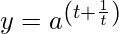
Differentiating it with respect to t using chain rule,
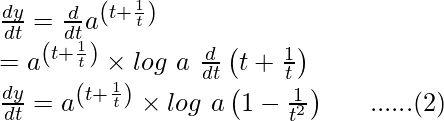
Dividing equation (2) by (1)
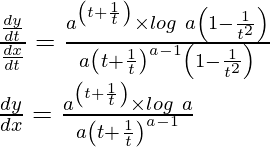
Share your thoughts in the comments
Please Login to comment...