Evaluate the following definite integrals:
Question 1. 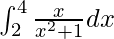
Solution:
We have,
I = 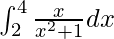
I = 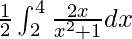
I = ![Rendered by QuickLaTeX.com \left[\frac{1}{2}\log(1+x^2)\right]_{2}^{4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-78d80c45316cbd2f4a30a9f5a16cedc2_l3.png)
I = 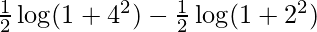
I = 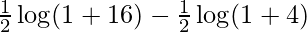
I = 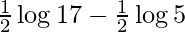
I = 
I = 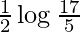
Therefore, the value of 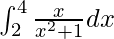 is
is 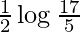 .
.
Question 2. 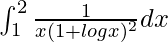
Solution:
We have,
I = 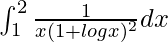
Let 1 + log x = t, so we have,
=> (1/x) dx = 2t dt
Now, the lower limit is, x = 1
=> t = 1 + log x
=> t = 1 + log 1
=> t = 1 + 0
=> t = 1
Also, the upper limit is, x = 2
=> t = 1 + log x
=> t = 1 + log 2
So, the equation becomes,
I = 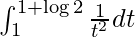
I = ![Rendered by QuickLaTeX.com \left[\frac{-1}{t}\right]_1^{1+\log2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25b3e971a25751b47fb527230aeadade_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{-1}{1+\log2}+1\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d35b75c7d7367fd24099c9486bc0fe2_l3.png)
I = 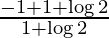
I = 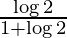
I = 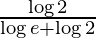
I = 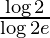
Therefore, the value of 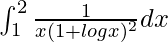 is
is 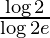 .
.
Question 3. 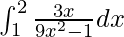
Solution:
We have,
I = 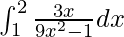
Let 9x2 – 1 = t, so we have,
=> 18x dx = dt
=> 3x dx = dt/6
Now, the lower limit is, x = 1
=> t = 9x2 – 1
=> t = 9 (1)2 – 1
=> t = 9 – 1
=> t = 8
Also, the upper limit is, x = 2
=> t = 9x2 – 1
=> t = 9 (2)2 – 1
=> t = 36 – 1
=> t = 35
So, the equation becomes,
I = 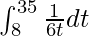
I = ![Rendered by QuickLaTeX.com \left[\frac{1}{6}\log t\right]_{8}^{35}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c5277715c0e5e9a793dabeea46147ae_l3.png)
I = 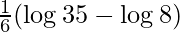
I = 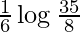
Therefore, the value of 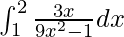 is
is 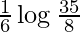 .
.
Question 4. 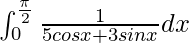
Solution:
We have,
I = 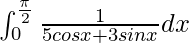
On putting sin x = 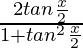 and cos x =
and cos x = 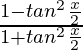 , we get
, we get
I = 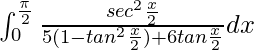
I = 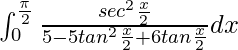
Let tan x/2 = t. So, we have
=> 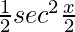 = dt
= dt
Now, the lower limit is, x = 0
=> t = tan x/2
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = tan x/2
=> t = tan π/4
=> t = 1
So, the equation becomes,
I = 
I = 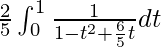
I = 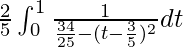
I = ![Rendered by QuickLaTeX.com \left[\frac{2}{5}.\frac{1}{2}\sqrt{\frac{25}{34}}\log\left(\frac{\sqrt{\frac{34}{25}}+t-\frac{3}{5}}{\sqrt{\frac{34}{25}}-t+\frac{3}{5}}\right)\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ffefeca712332617c5ad586720ae9be_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{2}{5}.\frac{1}{2}\frac{5}{\sqrt{34}}\log\left(\frac{\sqrt{\frac{34}{25}}+t-\frac{3}{5}}{\sqrt{\frac{34}{25}}-t+\frac{3}{5}}\right)\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-68db90d1bec6cb14c4c722672fa00d36_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{\sqrt{34}}\left[\log\left(\frac{\sqrt{34}+2}{\sqrt{34}-2}\right)-\log\left(\frac{\sqrt{34}-3}{\sqrt{34}+3}\right)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9f3f01be19d5e632a487df860e2459d0_l3.png)
I = 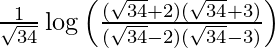
I = 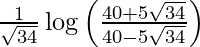
I = 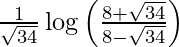
Therefore, the value of 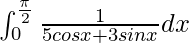 is
is 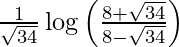 .
.
Question 5. 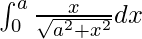
Solution:
We have,
I = 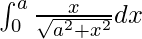
Let a2 + x2 = t2. So, we have
=> 2x dx = 2t dt
=> x dx = t dt
Now, the lower limit is, x = 0
=> t2 = a2 + x2
=> t2 = a2 + 02
=> t2 = a2
=> t = a
Also, the upper limit is, x = a
=> t2 = a2 + x2
=> t2 = a2 + a2
=> t2 = 2a2
=> t = √2 a
So, the equation becomes,
I = 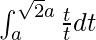
I = 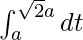
I = ![Rendered by QuickLaTeX.com \left[t\right]_{a}^{\sqrt{2}a}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2064e2744b718f65c6f30bb94a8113a4_l3.png)
I = √2a – a
I = a (√2 – 1)
Therefore, the value of 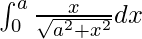 is a (√2 – 1).
is a (√2 – 1).
Question 6. 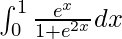
Solution:
We have,
I = 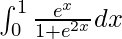
Let ex = t. So, we have
=> ex dx = dt
Now, the lower limit is, x = 0
=> t = ex
=> t = e0
=> t = 1
Also, the upper limit is, x = a
=> t = ex
=> t = e1
=> t = e
So, the equation becomes,
I = 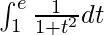
I = ![Rendered by QuickLaTeX.com \left[tan^{-1}t\right]_{1}^{e}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d5d9979eb3041a0a385a25229b04748a_l3.png)
I = 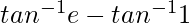
I = 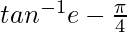
Therefore, the value of 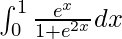 is
is 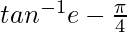 .
.
Question 7. 
Solution:
We have,
I = 
Let x2 = t. So, we have
=> 2x dx = dt
Now, the lower limit is, x = 0
=> t = x2
=> t = 02
=> t = 0
Also, the upper limit is, x = 1
=> t = x2
=> t = 12
=> t = 1
So, the equation becomes,
I = 
I = 
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[e^t\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a5d569fa296cdf5900797145d3a9233_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[e^1-e^0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ccce5e2de12eb09193a0a955ee2c6603_l3.png)
I = 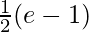
Therefore, the value of  is
is 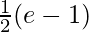 .
.
Question 8. 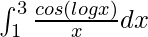
Solution:
We have,
I = 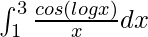
Let log x = t. So, we have
=> (1/x) dx = dt
Now, the lower limit is, x = 1
=> t = log x
=> t = log 1
=> t = 0
Also, the upper limit is, x = 3
=> t = log x
=> t = log 3
So, the equation becomes,
I = 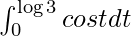
I = ![Rendered by QuickLaTeX.com \left[sint\right]_{0}^{\log3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9f18a1568db5f5b02f5a63ccb2e0bb65_l3.png)
I = sin (log 3) – sin 0
I = sin (log 3) – 0
I = sin (log 3)
Therefore, the value of 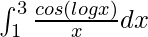 is sin (log 3).
is sin (log 3).
Question 9. 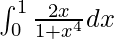
Solution:
We have,
I = 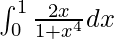
Let x2 = t. So, we have
=> 2x dx = dt
Now, the lower limit is, x = 0
=> t = x2
=> t = 02
=> t = 0
Also, the upper limit is, x = 1
=> t = x2
=> t = 12
=> t = 1
So, the equation becomes,
I = 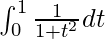
I = ![Rendered by QuickLaTeX.com \left[tan^{-1}t\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c3c4514c79c6a0bc58b7b3516f7eb3ab_l3.png)
I = 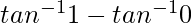
I = 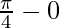
I = 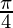
Therefore, the value of 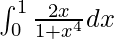 is
is 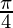 .
.
Question 10. 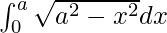
Solution:
We have,
I = 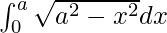
Let x = a sin t. So, we have
=> dx = a cos t dt
Now, the lower limit is, x = 0
=> a sin t = x
=> a sin t = 0
=> sin t = 0
=> t = 0
Also, the upper limit is, x = a
=> a sin t = a
=> a sin t = a
=> sin t = 1
=> t = π/2
So, the equation becomes,
I = 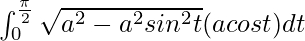
I = 
I = 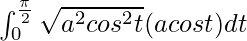
I = 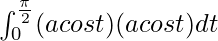
I = 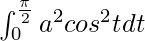
I = 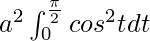
I = 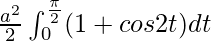
I = ![Rendered by QuickLaTeX.com \frac{a^2}{2}\left[t+\frac{sin2t}{2}\right]_{0}^{\frac{\pi}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b00f2eaec46b4cccd315fa51444d5da9_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{a^2}{2}\left[\frac{\pi}{2}+0-0-0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dd20ab078ce51d0fb415f1844989d3d1_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{a^2}{2}\left[\frac{\pi}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-879b13bec8f190c358e2ada3872c3d7b_l3.png)
I = 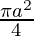
Therefore, the value of 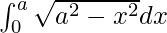 is
is 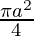 .
.
Question 11. 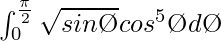
Solution:
We have,
I = 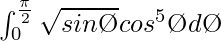
I = 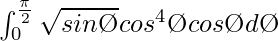
Let sin Ø = t. So, we have
=> cos Ø dØ = dt
Now, the lower limit is, Ø = 0
=> t = sin Ø
=> t = sin 0
=> t = 0
Also, the upper limit is, Ø = π/2
=> t = sin Ø
=> t = sin π/2
=> t = 1
So, the equation becomes,
I = 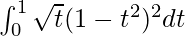
I = 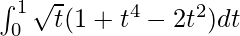
I = 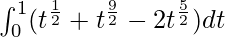
I = ![Rendered by QuickLaTeX.com \left[\frac{t^{\frac{1}{2}+1}}{\frac{1}{2}+1}+\frac{t^{\frac{9}{2}+1}}{\frac{9}{2}+1}-\frac{2t^{\frac{5}{2}+1}}{\frac{5}{2}+1}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bc93b726dbcf5435fe74436e3bf8e7ad_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{t^{\frac{3}{2}}}{\frac{3}{2}}+\frac{t^{\frac{11}{2}}}{\frac{11}{2}}-\frac{2t^{\frac{7}{2}}}{\frac{7}{2}}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aa5a36c05af5d28d5f12c8186335778e_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{2t^{\frac{3}{2}}}{3}+\frac{2t^{\frac{11}{2}}}{11}-\frac{4t^{\frac{7}{2}}}{7}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2cb28dbdbb96522d0f11921ed6ae81d8_l3.png)
I = 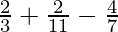
I = 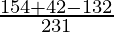
I = 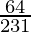
Therefore, the value of 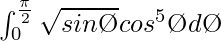 is
is 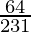 .
.
Question 12. 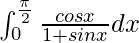
Solution:
We have,
I = 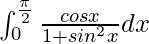
Let sin x = t. So, we have
=> cos x dx = dt
Now, the lower limit is, x = 0
=> t = sin x
=> t = sin 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = sin x
=> t = sin π/2
=> t = 1
So, the equation becomes,
I = 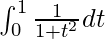
I = ![Rendered by QuickLaTeX.com \left[tan^{-1}t\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c3c4514c79c6a0bc58b7b3516f7eb3ab_l3.png)
I = 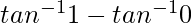
I = 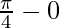
I = 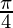
Therefore, the value of 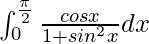 is
is 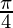 .
.
Question 13. 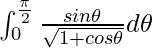
Solution:
We have,
I = 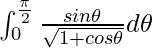
Let 1 + cos θ = t2. So, we have
=> – sin θ dθ = 2t dt
=> sin θ dθ = –2t dt
Now, the lower limit is, θ = 0
=> t2 = 1 + cos θ
=> t2 = 1 + cos 0
=> t2 = 1 + 1
=> t2 = 2
=> t = √2
Also, the upper limit is, θ = π/2
=> t2 = 1 + cos θ
=> t2 = 1 + cos π/2
=> t2 = 1 + 0
=> t2 = 1
=> t = 1
So, the equation becomes,
I = 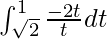
I = 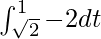
I = ![Rendered by QuickLaTeX.com -2\left[t\right]_{\sqrt{2}}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c1b9bd26c650017b88207bdca008806_l3.png)
I = ![Rendered by QuickLaTeX.com -2\left[1-\sqrt{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aeaba40aafda7884dd07d0c1f5c8e068_l3.png)
I = ![Rendered by QuickLaTeX.com 2\left[\sqrt{2}-1\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-72cbf39631061afa0e78f5d20af6890c_l3.png)
Therefore, the value of 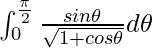 is
is ![Rendered by QuickLaTeX.com 2\left[\sqrt{2}-1\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-72cbf39631061afa0e78f5d20af6890c_l3.png) .
.
Question 14. 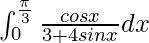
Solution:
We have,
I = 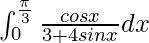
Let 3 + 4 sin x = t. So, we have
=> 0 + 4 cos x dx = dt
=> 4 cos x dx = dt
=> cos x dx = dt/4
Now, the lower limit is, x = 0
=> t = 3 + 4 sin x
=> t = 3 + 4 sin 0
=> t = 3 + 0
=> t = 3
Also, the upper limit is, x = π/3
=> t = 3 + 4 sin x
=> t = 3 + 4 sin π/3
=> t = 3 + 4 (√3/2)
=> t = 3 + 2√3
So, the equation becomes,
I = 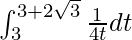
I = ![Rendered by QuickLaTeX.com \frac{1}{4}\left[\log t\right]_{3}^{3+2\sqrt{3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-180c818dd5270df4b981d1ea00184330_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{4}\left[\log (3+2\sqrt{3})-\log 3)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7f639a8bfd2687861bddcc3aa98ada0c_l3.png)
I = 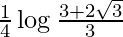
Therefore, the value of 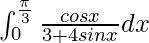 is
is 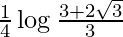 .
.
Question 15. 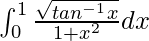
Solution:
We have,
I = 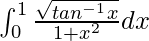
Let tan–1 x = t. So, we have
=> (1/1+x2) dx = dt
Now, the lower limit is, x = 0
=> t = tan–1 x
=> t = tan–1 0
=> t = 0
Also, the upper limit is, x = 1
=> t = tan–1 t
=> t = tan–1 1
=> t = π/4
So, the equation becomes,
I = 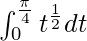
I = ![Rendered by QuickLaTeX.com \left[\frac{t^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]_{0}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f3b01acef7effcd383a4414f6f296c4c_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{t^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ef5ffffb2183d97f4a21a05ca300312f_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{2}{3}\left[t^{\frac{3}{2}}\right]_{0}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a51885dae198232d9917f6aebe5dec61_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{2}{3}\left[(\frac{\pi}{4})^{\frac{3}{2}}-0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e04e35cb371ebc973841f90d7efd65dd_l3.png)
I = 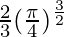
I = 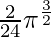
I = 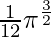
Therefore, the value of 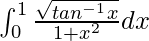 is
is 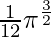 .
.
Question 16. 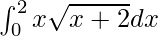
Solution:
We have,
I = 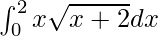
Let x + 2 = t2. So, we have
=> dx = 2t dt
Now, the lower limit is, x = 0
=> t2 = x + 2
=> t2 = 0 + 2
=> t2 = 2
=> t = √2
Also, the upper limit is, x = 2
=> t2 = x + 2
=> t2 = 2 + 2
=> t2 = 4
=> t = 2
So, the equation becomes,
I = 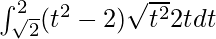
I = 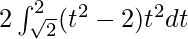
I = 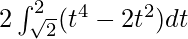
I = ![Rendered by QuickLaTeX.com 2\left[\frac{t^5}{5}-\frac{2t^3}{3}\right]_{\sqrt{2}}^{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bea2a7f4311c727086ab0a3a75ffd837_l3.png)
I = ![Rendered by QuickLaTeX.com 2\left[\frac{32}{5}-\frac{16}{3}-\frac{4\sqrt{2}}{5}+\frac{4\sqrt{2}}{3}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-837656c5fbc5c65a7b5c0135d0f8665d_l3.png)
I = ![Rendered by QuickLaTeX.com 2\left[\frac{16+8\sqrt{2}}{15}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5df7e9f85bba8b95cb60f48e490ecd53_l3.png)
I = ![Rendered by QuickLaTeX.com 2\left[\frac{8\sqrt{2}(1+\sqrt{2})}{15}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-69ff6ffd1a02d04a24cf31fcf86e9f29_l3.png)
I = 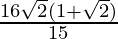
Therefore, the value of 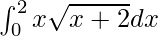 is
is 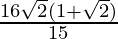 .
.
Question 17. 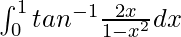
Solution:
We have,
I = 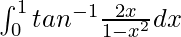
Let x = tan t. So, we have
=> dx = sec2 t dt
Now, the lower limit is, x = 0
=> tan t = x
=> tan x = 0
=> x = 0
Also, the upper limit is, x = 1
=> tan t = x
=> tan x = 1
=> x = π/4
So, the equation becomes,
I = 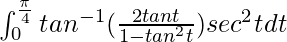
I = 
I = 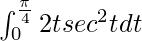
I = 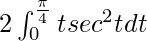
On applying integration by parts method, we get
I = ![Rendered by QuickLaTeX.com 2\left[t\int_0^\frac{\pi}{4}sec^2tdt-\int_0^\frac{\pi}{4}tantdt\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a13f24c2b63946affd232ed2ff90ffa1_l3.png)
I = ![Rendered by QuickLaTeX.com 2\left[ttant-log(cost)\right]^{\frac{\pi}{4}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-945e7ad644e26d5bc7ad81cade8dc71e_l3.png)
I = ![Rendered by QuickLaTeX.com 2\left[\frac{\pi}{4}+log\frac{1}{\sqrt{2}}-0-0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a4e6c4eed0cc3042c64b95d293d8918b_l3.png)
I = ![Rendered by QuickLaTeX.com 2\left[\frac{\pi}{4}+\frac{1}{2}log2\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-850cf1f121f9d907f79dfa1f16de72ec_l3.png)
I = 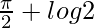
Therefore, the value of 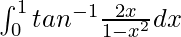 is
is 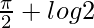 .
.
Question 18. 
Solution:
We have,
I = 
Let sin2 x = t. So, we have
=> 2 sin x cos x = dt
=> sin x cos x = dt/2
Now, the lower limit is, x = 0
=> t = sin2 x
=> t = sin2 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = sin2 x
=> t = sin2 π/2
=> t = 1
So, the equation becomes,
I = 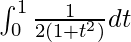
I = 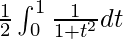
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[tan^{-1}t\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c0e17546ccd43b30f4be76b847c73a1b_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[tan^{-1}1-tan^{-1}0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7b23036b5689dd9a1e26a26c7334b986_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{\pi}{4}-0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7c67bfbffe89eeb575b8fb76f0ef6c82_l3.png)
I = 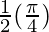
I = 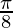
Therefore, the value of  is
is 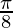 .
.
Question 19. 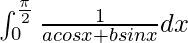
Solution:
We have,
I = 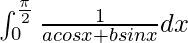
On putting cos x = 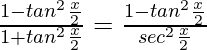 and sin x =
and sin x = 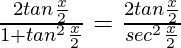 , we get,
, we get,
I = 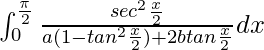
Let tan x/2 = t. So, we have
=> 1/2 sec2 x/2 dx = dt
=> sec2 x/2 dx = 2 dt
Now, the lower limit is, x = 0
=> t = tan x/2
=> t = tan 0/2
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = tan x/2
=> t = tan π/4
=> t = 1
So, the equation becomes,
I = 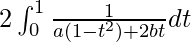
I = 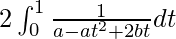
I = 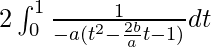
I = ![Rendered by QuickLaTeX.com \frac{2}{a}\int_{0}^{1}\frac{1}{-\left[(t-\frac{b}{a})^2-1-\frac{b^2}{a^2}\right]}dt](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cd1fc88c70f220397d2ba236435d41ac_l3.png)
I = 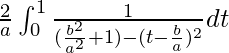
I = ![Rendered by QuickLaTeX.com \left[\frac{2}{a}\left(\frac{1}{2\sqrt{\frac{b^2+a^2}{a^2}}}\right)\log\left(\frac{\sqrt{\frac{b^2+a^2}{a^2}}+(t-\frac{b}{a})}{\sqrt{\frac{b^2+a^2}{a^2}}-(t-\frac{b}{a})}\right)\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a30ace3b32618a0d42bb0fe332d8da6_l3.png)
I = 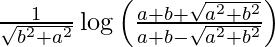
Therefore, the value of 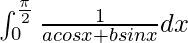 is
is 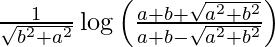 .
.
Question 20. 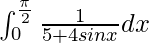
Solution:
We have,
I = 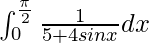
On putting sin x = 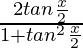 , we get
, we get
I = 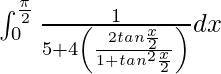
I = 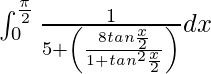
I = 
I = 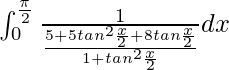
I = 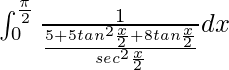
I = 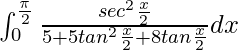
Let tan x/2 = t. So, we have
=> 1/2 sec2 x/2 dx = dt
=> sec2 x/2 dx = 2 dt
Now, the lower limit is, x = 0
=> t = tan x/2
=> t = tan 0/2
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = tan x/2
=> t = tan π/4
=> t = 1
So, the equation becomes,
I = 
I = 
I = 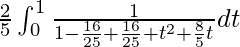
I = 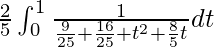
I = 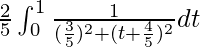
I = ![Rendered by QuickLaTeX.com \frac{2}{5}\left[\frac{5}{3}tan^{-1}\frac{5}{3}(t+\frac{4}{5})\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-abc9f86fc12e88d1e9363cfbd8ba5f57_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{2}{3}\left[tan^{-1}(\frac{5t}{3}+\frac{4}{3})\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7dcbb1933984fe4e66e6eaf1972cfbd1_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{2}{3}\left[tan^{-1}(\frac{5}{3}+\frac{4}{3})-tan^{-1}(0+\frac{4}{3})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7d234ef90a86fd9ee06e708f50e5e443_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{2}{3}\left[tan^{-1}(\frac{9}{3})-tan^{-1}(\frac{4}{3})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-016fb69579c02e50b402c7079cb88b99_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{2}{3}\left[tan^{-1}(3)-tan^{-1}(\frac{4}{3})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c5c16e7c96fe57256871b3bfae63e2a9_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{2}{3}\left[tan^{-1}(\frac{3-\frac{4}{3}}{1+3(\frac{4}{3})})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fa1b6716a734ea0c86bd55e23a64fb2b_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{2}{3}\left[tan^{-1}(\frac{\frac{5}{3}}{1+4})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-072ab951de16d2b16df17ee17c36cc79_l3.png)
I = 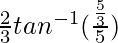
I = 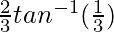
Therefore, the value of 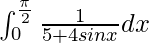 is
is 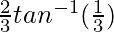 .
.
Share your thoughts in the comments
Please Login to comment...